2017-2018学年云南省云天化中学高二上学期阶段测试（一）数学试题（理科） 10页

云天化中学2017—2018学年度阶段测试（一）‎ 高二数学（理科）‎ 第Ⅰ卷（选择题，共60分）‎ 一、选择题（本大题共小题，每小题分．在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1、已知集合， ，则（ ）‎ ‎ ‎ ‎2、直线的倾斜角为（  ）‎ ‎    ‎ ‎3、在等差数列中，若、是方程的两个根，那么（ ）‎ ‎ ‎ ‎2‎ ‎4‎ ‎2‎ ‎2‎ 主视图 左视图 俯视图 ‎4、设为定义在上的奇函数，当时， ，则（ ）‎ ‎ ‎ ‎5、已知一个空间几何体的三视图如右图所示，根据图中标出的尺寸，可得这个几何体的体积是（ ）‎ ‎ ‎ ‎6、若满足约束条件，则的最大值为（ ）‎ ‎ ‎ ‎ 7、将函数的图象向左平移个单位后，得到函数的图象，则（ ）‎ ‎ ‎ 的图象关于对称 的图象关于 对称 ‎8、若直线与平行，则与的距离为（ ）‎ ‎ ‎ ‎9、甲、乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别为、,则下列判断正确的是（ ）‎ ‎ ，甲比乙成绩稳定 ，乙比甲成绩稳定 ‎，甲比乙成绩稳定 ，乙比甲成绩稳定 ‎10、执行如图所示的程序框图，则输出的（ ）‎ ‎ ‎ ‎11、直线过点且与以点、为端点的线段恒相交，则的斜率取值范围是（ ）‎ ‎ ‎ ‎ ‎ ‎12、若直线与圆的两个交点关于直线对称，则的值分别为（ ）‎ ‎ ‎ 第Ⅱ卷（非选择题，共90分）‎ ‎ 二、填空题（本大题共4小题，每空5分，共20分．）‎ ‎13、已知向量，若∥，则 ．‎ ‎14、直线恒经过定点 ．‎ ‎15、在中，，，，则 ．‎ ‎16、若直线，经过圆的圆心，则的最小值是 ．‎ 三、解答题（本题共6题，共70分．）‎ ‎17、（本小题满分10分）已知直线经过直线与直线的交点，且垂直于直线．‎ ‎（Ⅰ）求直线的方程；‎ ‎（Ⅱ）求直线与两坐标轴围成的三角形的面积．‎ ‎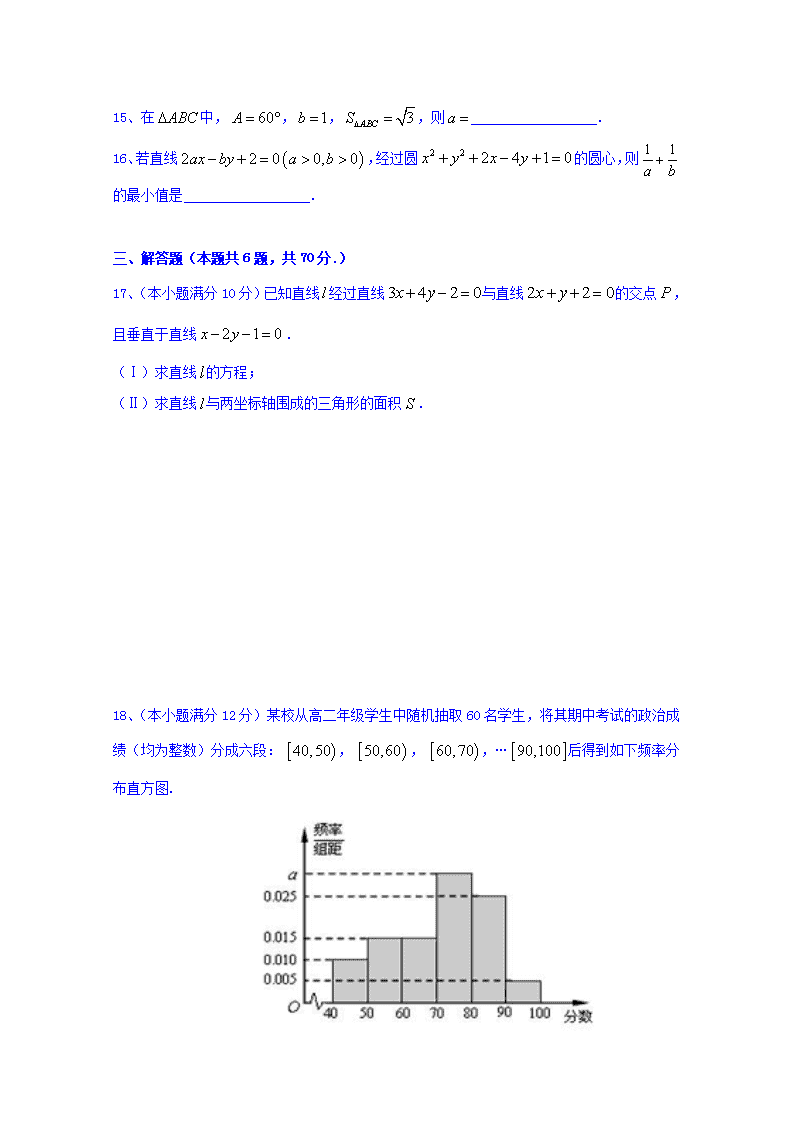18、（本小题满分12分）某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段： ， ， ，…后得到如下频率分布直方图.‎ ‎（Ⅰ）根据频率分布直方图，估计该校高二年级 学生期中考试政治成绩的平均分、众数、中位数；‎ ‎（小数点后保留一位有效数字）‎ ‎（Ⅱ）用分层抽样的方法在各分数段的学生中抽 取一个容量为的样本，则各分数段抽取的人数 分别是多少？‎ ‎19、（本小题满分12分）已知递增的等比数列和等差数列，满足， 是和的等差中项，且.‎ ‎（Ⅰ）求数列和的通项公式；‎ ‎（Ⅱ）若，数列的前项和，求证：.‎ ‎20、（本小题满分12分）在中，内角的对边分别为，且.‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）若，求，.‎ ‎21、（本小题满分12分）如图，四边形是边长为的菱形，平面为的中点.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）若，求多面体的体积.‎ ‎22、（本题满分12分）已知圆： ,直线： .‎ ‎（Ⅰ）求直线被圆所截得的弦长最短时的值及最短弦长；‎ ‎（Ⅱ）已知坐标轴上点和点满足：存在圆上的两点和，使得，求实数的取值范围.‎ 云天化中学2017—2018学年度阶段测试（一）‎ 高二年级理数答案 一、 选择题 题号 答案 二、填空题 题号 ‎13‎ ‎14‎ ‎15‎ ‎16‎ 答案 三、解答题 ‎17、（本小题满分10分）‎ ‎【解析】（Ⅰ）由解得则点坐标为．…………3分 由于点的坐标是，且所求直线与直线垂直，‎ 可设直线的方程为，把点的坐标代入得，…………5分 即，所求直线的方程为．……………………6分 ‎（Ⅱ）由直线的方程知它在轴、轴上的截距分别是、，……………………8分 所以直线与两坐标轴围成的三角形的面积．………………………………10分 考点：直线方程的求解及应用．‎ ‎18、（本小题满分12分）‎ ‎【解析】（Ⅰ）由图可知，……………‎ ‎1分 众数为，…………………………………………………………………………………………2分 设中位数为，则，所以中位数为，……4分 平均数为．…………6分 ‎（Ⅱ）各层抽取比例为，各层人数分别为6,9,9,18,15,3，所以抽取人数依次为2人；3人；3人；6人；5人；1人．……………………………………………………12分 ‎19、（本小题满分12分）‎ ‎【解析】试题分析：（1）利用等差数列等比数列基本公式求通项；（2）利用裂项相消法求和.‎ 试题解析：‎ ‎（Ⅰ）设等比数列的公比为，等差数列的公差为，……………………1分 由，解得，……………………………………3分 ‎∴，∴；…………………………………………4分 由题意知， ，则等差数列的公差 ‎,∴.……………………………………6分 ‎（Ⅱ）∵，……………………………8分 ‎∴ .…………10分 在上单调递增，又 ‎，即………………………………………………12分 ‎20、（本小题满分12分）‎ ‎【解析】试题分析：（Ⅰ）利用正弦定理可对进行化简，即可得到的值；（Ⅱ）利用正弦定理对进行化简，可得到，再利用的余弦定理，可求出的值.‎ 试题解析：（Ⅰ）由及正弦定理，得.………………2分 在中， .………………………………4分 ‎.……………………………………………………6分 ‎（Ⅱ）由及正弦定理，得，①………………………………8分 由余弦定理得， ，‎ 即，②………………………………10分 由①②，解得.…………………………12分 ‎21、（本小题满分12分）‎ 解：（Ⅰ）如图，连接交于，连接，………………2分 四边形是菱形，为的中点，又为的中点，‎ ‎………………6分 ‎（Ⅱ）四边形是边长为的菱形，，‎ ‎,由（Ⅰ）知，平面,,为的中点,,‎ ‎,……………………9分 ‎．…………12分 ‎22、（本小题满分12分）‎ 解：（Ⅰ）由，得，………………1分 ‎，‎ 所以直线恒过定点.………………………………………………2分 又，所以点在圆内，故当时，所截得的弦长最短，‎ 由题知圆心，半径 ‎，得，…………………………3分 所以由，得，………………………………………………4分 又圆心到直线的距离为 所以最短弦长为…………………………………………6分 ‎（Ⅱ）设， ，由，得，‎ 则有，…………………………………………………………………………7分 由在圆：上，得，‎ 由在圆上，得，…………………………………9分 所以圆： 与圆： 有交点，……………………10分 则有，…………………………………………………………11分 解得，‎ 故的取值范围为.………………………………………………………………12分