高一数学（人教A版）必修2能力强化提升：本册综合素质检测 14页

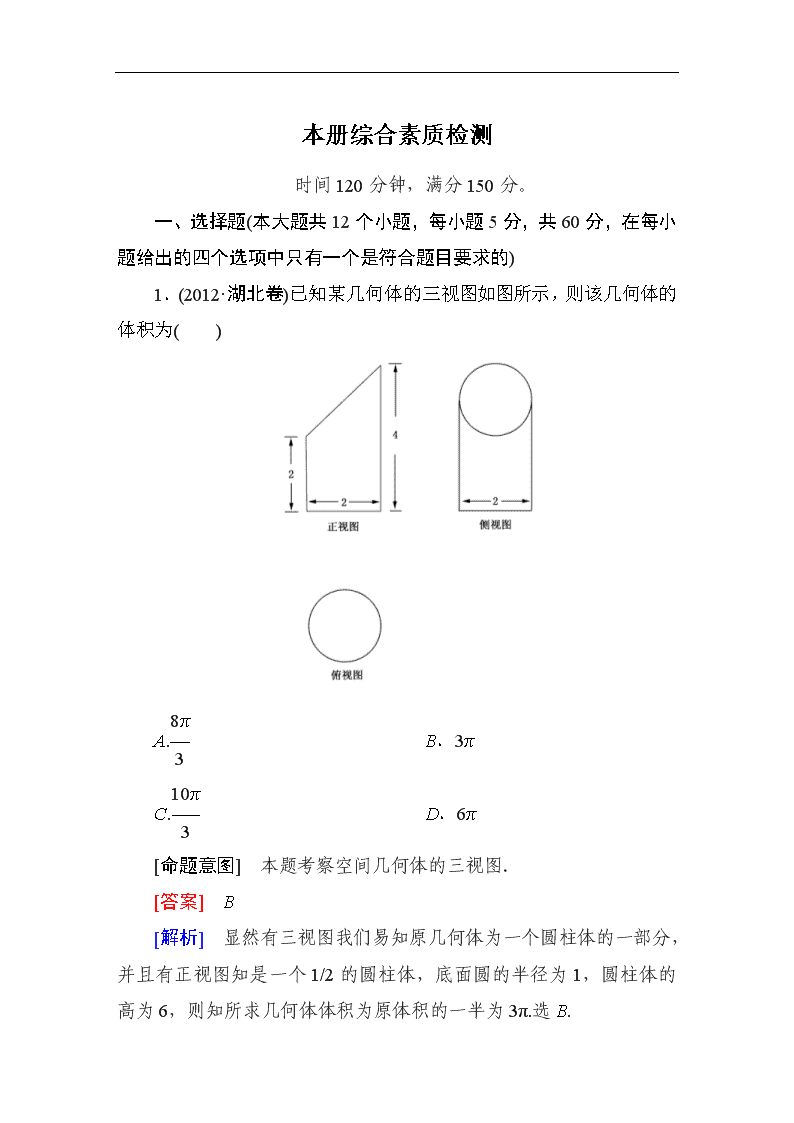
本册综合素质检测 时间 120 分钟，满分 150 分。 一、选择题(本大题共 12 个小题，每小题 5 分，共 60 分，在每小 题给出的四个选项中只有一个是符合题目要求的) 1．(2012·湖北卷)已知某几何体的三视图如图所示，则该几何体的 体积为( ) A.8π 3 B．3π C.10π 3 D．6π [命题意图] 本题考察空间几何体的三视图． [答案] B [解析] 显然有三视图我们易知原几何体为一个圆柱体的一部 分，并且有正视图知是一个 1/2 的圆柱体，底面圆的半径为 1，圆柱 体的高为 6，则知所求几何体体积为原体积的一半为 3π.选 B. 2．已知正方体外接球的体积是32 3 π，那么正方体的棱长等于( ) A．2 2 B.2 2 3 C.4 2 3 D.4 3 3 [答案] D [解析] 设正方体的棱长为 a，球的半径为 R，则4 3πR3＝32 3 π，∴R ＝2.又∵ 3a＝2R＝4，∴a＝4 3 3 . 3．直线 x－2y＋1＝0 关于直线 x＝1 对称的直线方程是( ) A．x＋2y－1＝0 B．2x＋y－1＝0 C．2x＋y－3＝0 D．x＋2y－3＝0 [答案] D [解析] 在所求直线上任取一点 P(x，y)，则点 P 关于直线 x＝1 的对称点为 P′(2－x，y)，且 P′在直线 x－2y＋1＝0 上，即 2－x－ 2y＋1＝0，整理得 x＋2y－3＝0，故选 D. 4．在空间直角坐标系中，O 为坐标原点，设 A(1 2 ，1 2 ，1 2)，B(1 2 ，1 2 ， 0)，C(1 3 ，1 3 ，1 3)，则( ) A．OA⊥AB B．AB⊥AC C．AC⊥BC D．OB⊥OC [答案] C [解析] |AB|＝1 2 ，|AC|＝ 3 6 ，|BC|＝ 6 6 ，因为|AC|2＋|BC|2＝|AB|2， 所以 AC⊥BC. 5．若 P(2，－1)为圆(x－1)2＋y2＝25 的弦 AB 的中点，则直线 AB 的方程为( ) A．x－y－3＝0 B．2x＋y－3＝0 C．x＋y－1＝0 D．2x－y－5＝0 [答案] A [解析] 设圆(x－1)2＋y2＝25 的圆心为 C(1,0)，则 AB⊥CP， ∵kCP＝－1，∴kAB＝1，∴y＋1＝x－2， 即 x－y－3＝0，故选 A. 6．已知 m，n 是两条不同直线，α，β，γ是三个不同平面，下列 命题中正确的是( ) A．若 m∥α，n∥α，则 m∥n B．若α⊥γ，β⊥γ，则α∥β C．若 m∥α，m∥β，则α∥β D．若 m⊥α，n⊥α，则 m∥n [答案] D [解析] A 中还可能 m，n 相交或异面，所以 A 不正确；B、C 中 还可能α，β相交，所以 B、C 不正确．很明显 D 正确． 7．如图，在长方体 ABCD－A1B1C1D1 中，M，N 分别是棱 BB1， B1C1 的中点，若∠CMN＝90°，则异面直线 AD1 和 DM 所成角为( ) A．30° B．45° C．60° D．90° [答案] D [解析] 因为 MN⊥DC，MN⊥MC，所以 MN⊥平面 DCM.所以 MN⊥DM. 因为 MN∥AD1，所以 AD1⊥DM. 8．(2012－2013·山东济宁模拟)已知直线 l 过点(－2,0)，当直线 l 与圆 x2＋y2＝2x 有两个交点时，其斜率 k 的取值范围是( ) A．(－2 2，2 2) B．(－ 2， 2) C．(－ 2 4 ， 2 4 ) D．(－1 8 ，1 8) [答案] C [解析] 设直线 l 的斜率为 k，则 l 的方程为 y＝k(x＋2)，即 kx－ y＋2k＝0，由于 l 与圆 x2＋y2＝2x 有两个交点，则需满足圆心到直线 的距离 d＝ |3k| k2＋1 ＜1，解得－ 2 4 ＜k＜ 2 4 . 9．在三棱柱 ABC－A1B1C1 中，各棱长相等，侧棱垂直于底面， 点 D 是侧面 BB1C1C 的中心，则 AD 与平面 BB1C1C 所成角的大小是 ( ) A．30° B．45° C．60° D．90° [答案] C [解析] 过 A 作 AE⊥BC 于点 E，则易知 AE⊥面 BB1C1C，则 ∠ADE 即为所求， 又 tan∠ADE＝AE DE ＝ 3，故∠ADE＝60°.故选 C. 10．过点 M(－2,4)作圆 C：(x－2)2＋(y－1)2＝25 的切线 l，且直 线 l1：ax＋3y＋2a＝0 与 l 平行，则 l1 与 l 间的距离是( ) A.8 5 B.2 5 C.28 5 D.12 5 [答案] D [解析] 因为点 M(－2,4)在圆 C 上，所以切线 l 的方程为(－2－ 2)(x－2)＋(4－1)(y－1)＝25， 即 4x－3y＋20＝0.因为直线 l 与直线 l1 平行， 所以－a 3 ＝4 3 ， 即 a＝－4，所以直线 l1 的方程是－4x＋3y－8＝0， 即4x－3y＋8＝0.所以直线l1与直线l间的距离为 |20－8| 42＋－32 ＝12 5 . 故选 D. 11．点 P(4，－2)与圆 x2＋y2＝4 上任一点连线的中点轨迹方程是 ( ) A．(x－2)2＋(y＋1)2＝1 B．(x－2)2＋(y－1)2＝4 C．(x－4)2＋(y－2)2＝1 D．(x－2)2＋(y－1)2＝1 [答案] A [ 解 析 ] 设 圆 上 任 意 一 点 为 (x1 ， y1) ， 中 点 为 (x ， y) ， 则 x＝x1＋4 2 y＝y1－2 2 ，x1＝2x－4 y1＝2y＋2 ，代入 x2＋y2＝4，得(2x－4)2＋(2y＋2)2 ＝4，化简得(x－2)2＋(y＋1)2＝1. 12 ． 设 P(x ， y) 是 圆 x2 ＋ (y ＋ 4)2 ＝ 4 上 任 意 一 点 ， 则 x－12＋y－12的最小值为( ) A. 26＋2 B. 26－2 C．5 D．6 [答案] B [解析] 如图，设 A(1,1)， x－12＋y－12 ＝|PA|，则|PA|的最小值为|AC|－r＝ 26－2. 三、填空题(本大题共 4 小题，每小题 5 分，共 20 分) 13．顺次连结 A(1,0)，B(1,4)，C(3,4)，D(5,0)所得到的四边形绕 y 轴旋转一周，所得旋转体的体积是________． [答案] 184π 3 [解析] 所得旋转体的上底、下底分别为 3,5，高为 4 的圆台，去 掉一个半径为 1，高为 4 的圆柱．V 台＝1 3(9π＋ 9π×25π＋25π)×4＝ 196π 3 ，V 柱＝4π，则 V＝V 台－V 柱＝184π 3 . 14．经过点 P(1,2)的直线，且使 A(2,3)，B(0，－5)到它的距离相 等的直线方程为________． [答案] 4x－y－2＝0 或 x＝1 [解析] x＝1 显然符合条件；当 A(2,3)，B(0，－5)在所求直线同 侧时，所求直线与 AB 平行， ∵kAB＝4，∴y－2＝4(x－1)， 即 4x－y－2＝0. 15．圆 x2＋y2＋Dx＋Ey＋F＝0 关于直线 l1：x－y＋4＝0 与直线 l2：x＋3y＝0 都对称，则 D＝________，E＝________. [答案] 6 －2 [解析] 由题设知直线 l1，l2 的交点为已知圆的圆心． 由 x－y＋4＝0， x＋3y＝0， 得 x＝－3， y＝1， 所以－D 2 ＝－3，D＝6，－E 2 ＝1，E＝－2. 16．已知圆 C 过点(1,0)，且圆心在 x 轴的正半轴上，直线 l：y＝ x－1 被圆 C 所截得的弦长为 2 2，则过圆心且与直线 l 垂直的直线的 方程为________． [答案] x＋y－3＝0 [解析] 设圆心(a,0)(a＞0)， ∴(|a－1| 2 )2＋( 2)2＝|a－1|2.∴a＝3. ∴圆心(3,0)． ∴所求直线方程为 x＋y－3＝0. 四、解答题(本大题共 6 小题，共 70 分，解答应写出文字说明， 证明过程或演算步骤) 17．(本小题满分 10 分)(2011·课标全国高考，文 18)如图，四棱锥 P－ABCD 中，底面 ABCD 为平行四边形，∠DAB＝60°，AB＝2AD， PD⊥底面 ABCD. (1)证明 PA⊥BD； (2)设 PD＝AD＝1，求棱锥 D－PBC 的高． [解析] (1)证明：因为∠DAB＝60°，AB＝2AD， 由余弦定理得 BD＝ 3AD. 从而 BD2＋AD2＝AB2， 故 BD⊥AD. 又 PD⊥底面 ABCD，可得 BD⊥PD. 所以 BD⊥平面 PAD.故 PA⊥BD. (2)如图，作 DE⊥PB，垂足为 E. 已知 PD⊥底面 ABCD， 则 PD⊥BC. 由(1)知 BD⊥AD， 又 BC∥AD，所以 BC⊥BD. 故 BC⊥平面 PBD， 所以 BC⊥DE. 则 DE⊥平面 PBC. 由题设知 PD＝1，则 BD＝ 3，PB＝2. 根据 DE·PB＝PD·BD，得 DE＝ 3 2 ， 即棱锥 D－PBC 的高为 3 2 . 18．(本小题满分 12 分)如图，矩形 ABCD 的两条对角线相交于点 M(2,0)，AB 边所在直线的方程为 x－3y－6＝0，点 T(－1,1)在 AD 边 所在直线上． (1)求 AD 边所在直线的方程； (2)求矩形 ABCD 外接圆的方程． [解析] (1)因为 AB 边所在直线的方程为 x－3y－6＝0，且 AD 与 AB 垂直，所以直线 AD 的斜率为－3.又因为点 T(－1,1)在直线 AD 上， 所以 AD 边所在直线的方程为 y－1＝－3(x＋1)，即 3x＋y＋2＝0. (2)由 x－3y－6＝0 3x＋y＋2＝0 ，解得点 A 的坐标为(0，－2)．因为矩形 ABCD 两条对角线的交点为 M(2,0)，所以 M 为矩形 ABCD 外接圆的 圆心．又 r＝|AM|＝ 2－02＋0＋22＝2 2.所以矩形 ABCD 外接圆的 方程为(x－2)2＋y2＝8. 19．(本小题满分 12 分)已知圆的半径为 10，圆心在直线 y＝2x 上，圆被直线 x－y＝0 截得的弦长为 4 2，求圆的方程． [解析] 方法一：设圆的方程是(x－a)2＋(y－b)2＝10.因为圆心在 直线 y＝2x 上，所以 b＝2a. ① 解方程组 x－y＝0， x－a2＋y－b2＝10， 得 2x2－2(a＋b)x＋a2＋b2－10＝0， 所以 x1＋x2＝a＋b，x1·x2＝a2＋b2－10 2 . 由弦长公式得 2· a＋b2－2a2＋b2－10 ＝4 2， 化简得(a－b)2＝4. ② 解①②组成的方程组，得 a＝2，b＝4， 或 a＝－2，b＝－4. 故所求圆的方程是(x－2)2＋(y－4)2＝10， 或(x＋2)2＋(y＋4)2＝10. 方法二：设圆的方程为(x－a)2＋(y－b)2＝10，则圆心为(a，b)， 半径 r＝ 10，圆心(a，b)到直线 x－y＝0 的距离 d＝|a－b| 2 . 由弦长、弦心距、半径组成的直角三角形得 d2＋(4 2 2 )2＝r2，即 a－b2 2 ＋8＝10， 所以(a－b)2＝4. 又因为 b＝2a，所以 a＝2，b＝4， 或 a＝－2，b＝－4. 故所求圆的方程是(x－2)2＋(y－4)2＝10， 或(x＋2)2＋(y＋4)2＝10. 20．(本小题满分 12 分)(2012·山东卷) 如图，几何体 E－ABCD 是四棱锥，△ABD 为正三角形，CB＝ CD，EC⊥BD. (1)求证：BE＝DE； (2)若∠BCD＝120°，M 为线段 AE 的中点，求证：DM∥平面 BEC. [解析] (1)设 BD 中点为 O，连接 OC，OE，则由 BC＝CD 知，CO⊥BD， 又已知 CE⊥BD，所以 BD⊥平面 OCE. 所以 BD⊥OE，即 OE 是 BD 的垂直平分线， 所以 BE＝DE. (2)取 AB 中点 N，连接 MN，DN， ∵M 是 AE 的中点，∴MN∥BE， ∵△ABD 是等边三角形，∴DN⊥AB. 由∠BCD＝120°知，∠CBD＝30°，所以∠ABC＝60°＋30°＝90°， 即 BC⊥AB， 所以 ND∥BC， 所以平面 MND∥平面 BEC，故 DM∥平面 BEC. 21．(本小题满分 12 分)在平面直角坐标系 xOy 中，已知圆 C1：(x －4)2＋(y－5)2＝4 和圆 C2：(x＋3)2＋(y－1)2＝4. (1)若直线 l1 过点 A(2,0)，且与圆 C1 相切，求直线 l1 的方程； (2)直线 l2 的方程是 x＝5 2 ，证明：直线 l1 上存在点 P，满足过 P 的 无穷多对互相垂直的直线 l3 和 l4，它们分别与圆 C1 和圆 C2 相交，且 直线 l3 被圆 C1 截得的弦长与直线 l4 被圆 C2 截得的弦长相等． [解析] (1)若直线斜率不存在，x＝2 符合题意； 当直线 l1 的斜率存在时， 设直线 l1 的方程为 y＝k(x－2)， 即 kx－y－2k＝0， 由条件得|4k－5－2k| k2＋1 ＝2， 解得 k＝21 20 ， 所以直线 l1 的方程为 x＝2 或 y＝21 20(x－2)， 即 x＝2 或 21x－20y－42＝0. (2)由题意知，直线 l3，l4 的斜率存在，设直线 l3 的斜率为 k，则 直线 l4 的斜率为－1 k ， 设点 P 坐标为(5 2 ，n)，互相垂直的直线 l3，l4 的方程分别为：y－n ＝k(x－5 2)，y－n＝－1 k(x－5 2)， 即 kx－y＋n－5 2k＝0，－1 kx－y＋n＋ 5 2k ＝0， 根据直线 l3 被圆 C1 截得的弦长与直线 l4 被圆 C2 截得的弦长相等， 两圆半径相等．由垂径定理得：圆心 C1 到直线 l3 与圆心 C2 到直线 l4 的距离相等． 故有|4k－5＋n－5 2k| k2＋1 ＝ |3 k －1＋n＋ 5 2k| 1 k2＋1 ， 化简得(5 2 －n)k＝21 2 －n 或 (1 2 ＋n)k＝－n－1 2 ＝－(1 2 ＋n)． 关于 k 的方程有无穷多解， 有1 2 ＋n＝0，即 n＝－1 2 ， 即直线 l2 上满足条件的点 P 是存在的，坐标是(5 2 ，－1 2)． 22．(本小题满分 12 分)(2013·全国高考卷Ⅱ文科 18 题)如图已知 三棱柱 ABC－A1B1C1 中，D、E 分别是 AB、BB1 的中点． (1)证明：BC1∥面 A1CD1； (2)设 AA1＝AC＝CB＝2，AB＝2 2，求三棱锥 C－A1DE 的体积． [解析] (1)连结 AC1 交 A1C 于点 F，则 F 为 AC1 的中点，又 D 是 AB 中点，连结 DF，则 BC1∥DF，因为 DF⊂平面 A1CD，BC1⊄平面 A1CD，所以 BC1∥平面 A1CD. (2)因为 ABC－A1B1C1 是直三棱柱，所以 AA1⊥CD，由已知 AC ＝CB，D 为 AB 中点，所以，CD⊥AB，又 AA1∩AB＝A，于是 CD⊥ 平面 ABB1A1，由 AA1＝AC＝CB＝2，AB＝2 2得，∠ACB＝90°， CD＝ 2，A1D＝ 6，DE＝ 3，A1E＝3，故 A1D2＋DE2＝A1E2，即 DE⊥A1D，所以 VC－A1DE＝1 3 ×1 2 × 6× 3× 2＝1.