数学文卷·2018届福建省南平市高三上学期第一次综合质量检查（2月）（2018 12页

‎2018年南平市普通高中毕业班第一次综合质量检查 数学（文）试题 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 设，则（ ）‎ A． B． C． D．‎ ‎2.某人到甲、乙两市各7个小区调査空置房情况，调查得到的小区空置房的套数绘成了如图的茎叶图，则调査中甲市空置房套数的中位数与乙市空置房套数的众数之差为（ ）‎ A．4 B．‎3 C．2 D．1‎ ‎3.已知复数满足(为虚数单位)，则的虚部为（ ）‎ A． B． C． D．‎ ‎4.在锐角中，角所对的边长分别为，，则角等于（ ）‎ A． B． C． D．‎ ‎5.中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还.”其大意为:“有一个人走了 378里路，第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了 6天后到达目的地.”则此人第4天走了（ ）‎ A．60里 B．48里 C．36里 D．24里 ‎ ‎6.已知函数，若，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎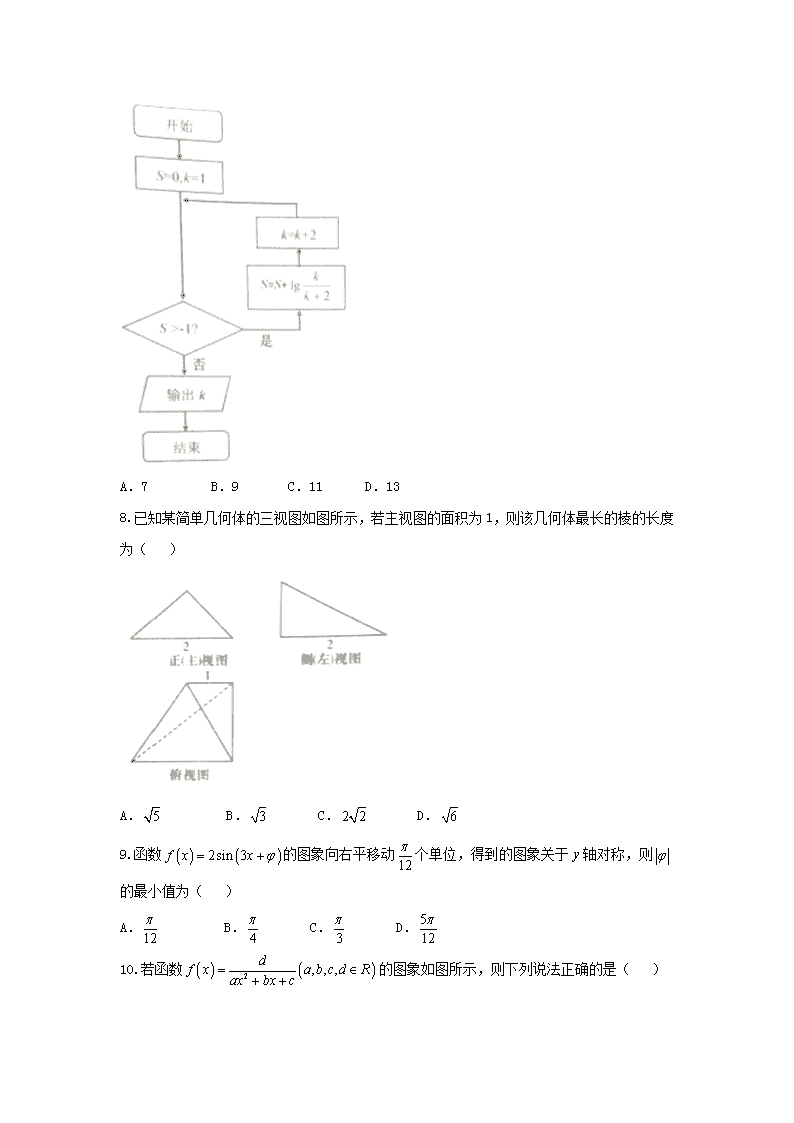7.执行如图所示的程序框图，则输出的的值为（ ）‎ A．7 B．‎9 C．11 D．13‎ ‎8.已知某简单几何体的三视图如图所示，若主视图的面积为1，则该几何体最长的棱的长度为（ ）‎ A． B． C． D．‎ ‎9.函数的图象向右平移动个单位，得到的图象关于轴对称，则的最小值为（ ）‎ A． B． C． D．‎ ‎10.若函数的图象如图所示，则下列说法正确的是（ ）‎ A． B． ‎ C． D．‎ ‎11.已知直线与双曲线的一条渐近线平行，且这两条平行线间的距离为1，则双曲线的离心率为（ ）‎ A．2 B． C．3 D．‎ ‎12.已知可导函数的导函数为，，若对任意的，都有，则不等式的解集为（ ）‎ A． B． C． D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13. 已知满足，则的最大值为 ．‎ ‎14.已知向量，且，则等于 ．‎ ‎15.已知点是抛物线上一点，为抛物线的焦点，则以为圆心，为半径的圆被直线截得的弦长为 ．‎ ‎16.正方体的外接球的表面积为，为球心，为的中点.点在该正方体的表面上运动，则使的点所构成的轨迹的周长等于 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 已知等差数列满足,前7项和为.‎ ‎（1）求的通项公式；‎ ‎（2）设数列满足，求的前项和.‎ ‎18.三棱锥中，侧面底面,是等腰直角三角形的斜边，且.‎ ‎（1）求证：；‎ ‎（2）已知平面平面，平面平面，，且到平面的距离相等，试确定直线及点的位置（说明作法及理由），并求三棱锥的体积.‎ ‎19. 有甲、乙两个桔柚（球形水果）种植基地，已知所有采摘的桔柚的直径都在范围内（单位：毫米，以下同），按规定直径在内为优质品，现从甲、乙两基地所采摘的桔柚中各随机抽取500个，测量这些桔柚的直径，所得数据整理如下：‎ ‎（1）根据以上统计数据完成下面列联表，并回答是否有以上的把握认为“桔柚直径与所在基地有关”？‎ ‎（2）求优质品率较高的基地的500个桔柚直径的样本平均数(同一组数据用该区间的中点值作代表)；‎ ‎（3）记甲基地直径在范围内的五个桔柚分别为，现从中任取二个，求含桔柚的概率.‎ 附：，.‎ ‎20．已知分别是椭圆的左、右焦点，是椭圆上一点，且.‎ ‎（1）求椭圆的方程；‎ ‎（2）设直线与椭圆交于两点，且，试求点到直线的距离.‎ ‎21.已知函数，其中.‎ ‎（1）试讨论函数的单调性及最值；‎ ‎（2）若函数不存在零点，求实数的取值范围.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.选修4-4：坐标系与参数方程 在直角坐标系中，圆的参数方程为（为参数).以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.‎ ‎（1）求圆的极坐标方程和直线的直角坐标方程；‎ ‎（2）设|与的交点为，求的面积.‎ ‎23.选修4-5：不等式选讲 已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若对任意实数恒成立，求实数的取值范围.‎ ‎2018年南平市普通高中毕业班第一次综合质量检查 文科数学试题答案及评分参考 说明：‎ ‎1、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则.‎ ‎2、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分.‎ ‎3、只给整数分数. 选择题和填空题不给中间分.‎ 一、选择题：本题考查基础知识和基本运算，每小题5分，满分60分．‎ ‎（1）B （2）B （3）A （4） C （5）D （6） C ‎（7）C （8）C （9）B （10）D （11）D （12）A 二、填空题：本题考查基础知识和基本运算，每小题5分，满分20分．‎ ‎（13） （14） （15） （16） ‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．‎ ‎ ‎ ‎（17）（满分12分）‎ 解：（Ⅰ）由，得……………（2分）‎ 因为所以…………（4分）‎ ‎……………（6分）‎ ‎（Ⅱ）‎ ‎……………（7分）‎ ‎……………（9分）‎ ‎…………（11分）‎ ‎……………（12分）‎ ‎（18）（满分12分）‎ S C A B D D O 解析:（Ⅰ）法一:在内作，交于，连结，‎ 则由侧面底面， ‎ 得底面……………（2分）‎ 又，，‎ ‎，为等腰直角三角形，，‎ 又∩=,…………（5分）‎ 即…………（6分）‎ 法二:取中点，连结,,由侧面底面 得,…………（2分）‎ 由已知,‎ ‎，‎ 又∩=,…………（5分）‎ 即…………（6分）‎ ‎（Ⅱ）法一:‎ 平面∥平面,平面∩平面,平面∩平面 ‎…………（7分）‎ 到平面的距离相等//平面或中点在平面上 又平面,平面∩平面 ‎//或中点在上,‎ 或为平行四边形,即.…………（9分）‎ 所以,过点A在平面ABC内作直线平行于BC，则所作直线即为l,以A为圆心BC长为半径作弧与l交点即为点(或在l上到A距离为2的点即为点)…………（10分）‎ 其中…………（12分）‎ 法二:到平面的距离相等…………（8分）‎ 平面∥平面，平面∩平面，平面∩平面 ‎//或中点在上,‎ 或为平行四边形,即.……（11分）‎ 所以,过点A在平面ABC内作直线平行于BC，则所作直线即为l,以A为圆心BC长为半径作弧与l交点即为点(或在l上到A距离为2的点即为点)…………（12分）‎ ‎（19）（满分12分）‎ 解：（Ⅰ）由以上统计数据填写列联表如下：‎ 甲基地 乙基地 合计 优质品 ‎420‎ ‎390‎ ‎810‎ 非优质品 ‎80‎ ‎110‎ ‎190‎ 合计 ‎500‎ ‎500‎ ‎1000‎ ‎……………（2分）‎ ‎，‎ 所以,有95%的把握认为：“桔柚直径与所在基地有关”． ……………（4分）‎ ‎（Ⅱ）甲基地桔柚的优质品率为，乙基地桔柚的优质品率为，‎ 所以，甲基地桔柚的优质品率较高，……………（5分）‎ 甲基地的500个桔柚直径的样本平均数…（6分）‎ ‎ …………（8分）‎ ‎（Ⅲ）依题意：记“从甲基地直径在的五个桔柚A,B,C,D,E中任取二个，含桔柚A”为事件N.‎ 实验包含的所有基本事件：（A,B）,（A,C），（A，D），（A，E），（B，C），（B，D），‎ ‎（B，E）,（C, D），（C，E），（D，E）共10种.…………（9分）‎ 事件N包含的结果有：（A, B）,（A, C），（A，D），（A，E）共4种.…………（10分）‎ 所求事件的概率为： …………（12分）‎ ‎（20）（满分12分）‎ 解：（Ⅰ）由得:，化简得：，‎ 解得：或…………（2分）‎ 因为，所以，…………（3分）‎ 因为 ‎ 所以，则，又，…………（4分）‎ 所以椭圆的标准方程为：；…………（5分）‎ ‎（Ⅱ）由题意可知，直线不过原点，设，‎ ① 直线轴，直线的方程且，‎ 则 ‎ 由得: ,‎ 即，解得：，‎ 故直线的方程为，∴原点到直线的距离，…………（7分）‎ ‎②当直线的斜率存在时，设直线的方程为，‎ 则，消去整理得：，‎ ‎，，…………（8分）‎ 则=‎ 由得, ‎ 故+，‎ 整理得：，‎ 即 ①…………（10分）‎ 原点到直线的距离，②…………（11分）‎ 将①代入②，则，∴，‎ 综上可知：原点到直线的距离．…………（12分）‎ ‎（21）（满分12分）‎ 解：（Ⅰ）由 得：‎ ‎ ………2分 ⑴当时, 在单调递增，‎ 没有最大值，也没有最小值.………3分 ⑵若，‎ 当时, , 在单调递增………4分 ‎ 当时， , 在单调递减，………5分 ‎ 所以当时，取到最大值 ‎ 没有最小值.………6分 ‎（Ⅱ） ‎ 由 ……8分 ‎ 当 时, , 单调递增，‎ ‎ 当时， , 单调递减，‎ 所以当时 ，取到最大值, ……10分 ‎ 又 时， 有 ，‎ ‎ 所以要使没有零点，‎ ‎ 只需 ……11分 ‎ 所以实数的取值范围是： ……12分 ‎（22）解:（Ⅰ）直线的直角坐标方程为……………………………2分 圆的普通方程为因为,‎ 所以 的极坐标方程为……………………5分 ‎（Ⅱ）将代入,得,解得,故,即.………………………8分 由于圆的半径为,所以的面积为………………………10分 ‎（23）解：（Ⅰ）‎ ‎ …………………………1分 ‎ 得 ，不合题意，舍去…………………2分 ① ② ‎ 得 ，……………3分 ③ ‎ 得 ，……………4分 综上不等式的解集为…………………5分 ‎（Ⅱ）由（Ⅰ）知，则…………………7分 则，解得…………………9分 即实数的取值范围是…………………10分