河南省六市2020届高三第一次模拟调研试题（4月） 数学（理） 13页

‎2020年河南省六市高三第一次模拟调研试题 理科数学 注意事项：‎ ‎1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分，满分150分。考试用时120分钟。‎ ‎2.答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、考试科目填写在规定的位置上。‎ ‎3.第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。‎ ‎4.第II卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。‎ 第I卷 选择题(共60分)‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有，一项是符合题目要求的。‎ ‎1.若复数z满足(1＋i)＝1＋2i，则|z|＝‎ A. B. C. D.‎ ‎2.集合M＝{y|y＝，x∈Z}的真子集的个数为 A.7 B.8 C.31 D.32‎ ‎3.五行学说是华夏民族创造的哲学思想，是华夏文明重要组成部分古人认为，天下万物皆由金、木、水、火、土五类元素组成，如图，分别是金、木、水、火、土彼此之间存在的相生相克的关系。若从五类元素中任选两类元素，则两类元素相生的概率为 A. B. C. 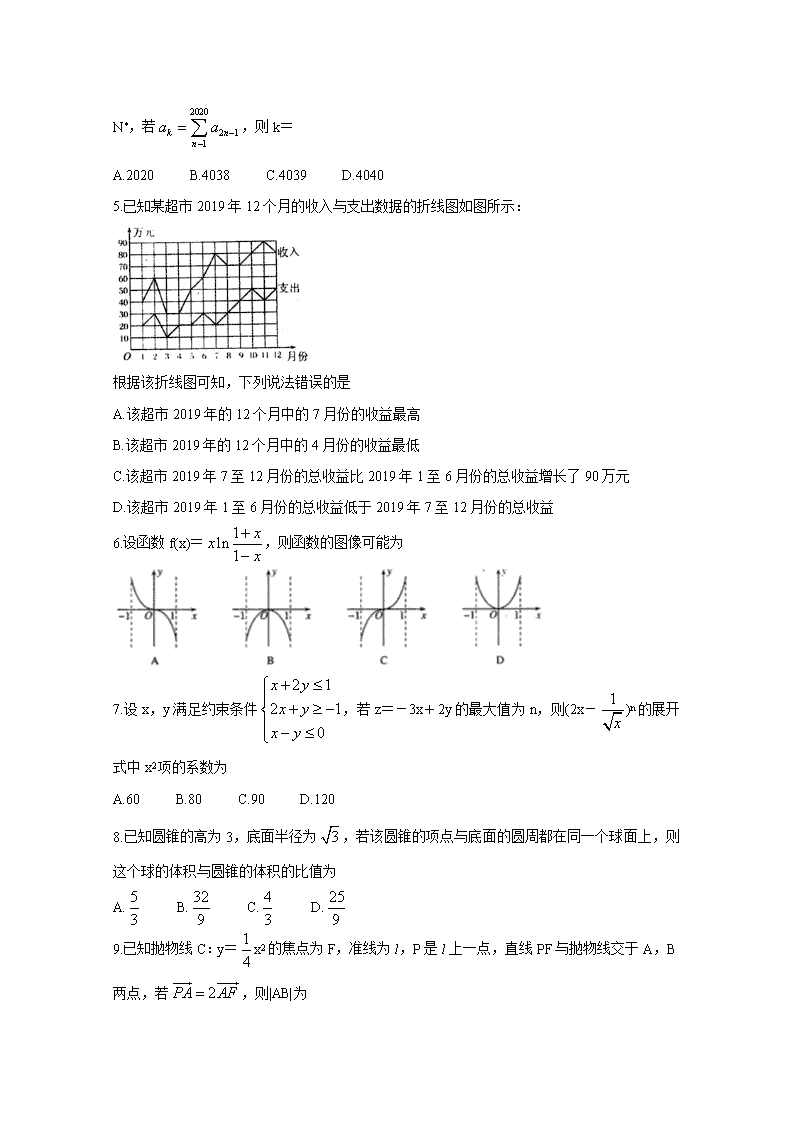D.‎ ‎4.著名的斐波那契数列{an}：1，1，2，3，5，8，…，满足a1＝a2＝1，an＋2＝an＋1＋an，n∈‎ N*，若，则k＝‎ A.2020 B.4038 C.4039 D.4040‎ ‎5.已知某超市2019年12个月的收入与支出数据的折线图如图所示：‎ 根据该折线图可知，下列说法错误的是 A.该超市2019年的12个月中的7月份的收益最高 B.该超市2019年的12个月中的4月份的收益最低 C.该超市2019年7至12月份的总收益比2019年1至6月份的总收益增长了90万元 D.该超市2019年1至6月份的总收益低于2019年7至12月份的总收益 ‎6.设函数f(x)＝，则函数的图像可能为 ‎7.设x，y满足约束条件，若z＝－3x＋2y的最大值为n，则(2x－)n的展开式中x2项的系数为 A.60 B.80 C.90 D.120‎ ‎8.已知圆锥的高为3，底面半径为，若该圆锥的项点与底面的圆周都在同一个球面上，则这个球的体积与圆锥的体积的比值为 A. B. C. D.‎ ‎9.已知抛物线C：y＝x2的焦点为F，准线为l，P是l上一点，直线PF与抛物线交于A，B两点，若，则|AB|为 A. B.40 C.16 D.‎ ‎10.已知P为圆C：(x－5)2＋y2＝36上任意一点，A(－5，0)，若线段PA的垂直平分线交直线PC于点Q，则Q点的轨迹方程为 A. B.‎ C. D.‎ ‎11.已知Sn是等差数列{an}的前n项和，若S2018f(－3x)的x的取值范围为 。‎ ‎15.六位同学坐在一排，现让六位同学重新坐，恰有两位同学坐自己原来的位置，则不同的坐法有 种(用数字回答)。‎ ‎16.若方程ax＝x(a>0且a≠1)有两个不等实根，则实数a的取值范围为 。‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎(一)必考题：60分。‎ ‎17.如图△ABC中，D为BC的中点，AB＝2，AC＝4，AD＝3。‎ ‎(1)求边BC的长；‎ ‎(2)点E在边AB上，若CE是∠BCA的角平分线，求△BCE的面积。‎ ‎18.(本小题满分12分)‎ 在四棱椎P－ABCD中，四边形ABCD为菱形，PA＝5，PB＝，AB＝6，PO⊥AD，O，E分别为AD，AB中点，∠BAD＝60°。‎ ‎(1)求证：AC⊥PE；‎ ‎(2)求平面POE与平面PBD所成锐二面角的余弦值。‎ ‎19.(本小题满分12分)‎ 设椭圆C：的左，右焦点分别为F1，F2，离心率为e，动点P(x0，y0)在椭圆C上运动，当PF2⊥x轴时，x0＝1，y0＝e。‎ ‎(1)求椭圆C的方程；‎ ‎(2)延长PF1，PF2分别交椭圆C于A，B(A，B不重合)两点，设，，求λ＋μ的最小值。‎ ‎20.(本小题满分12分)‎ 已知函数f(x)＝xex－ae2x(a∈R)在定义域内有两个不同的极值点。‎ ‎(1)求实数a的取值范围；。‎ ‎(2)若f(x)有两个不同的极值点x1，x2且x10恒成立，求正实数λ的取值范围。‎ ‎21.(本小题满分12分)‎ 某大型公司为了切实保障员工的健康安全，贯彻好卫生防安工作的相关要求，‎ 决定在全公司范围内举行一次NCP普查，为此需要抽验1000人的血样进行化验，由于人数较多，检疫部门制定了下列两种可供选择的方案。‎ 方案①：将每个人的血分别化验，这时需要验1000次。‎ 方案②：按k个人一组进行随机分组，把从每组k个人抽来的血混合在一起进行检验，如果每个人的血均为阴性，则验出的结果呈阴性，这k个人的血只需检验一次(这时认为每个人的血化验次)；否则，若呈阳性，则需对这k个人的血样再分别进行一次化验，这样，该组k个人的血总共需要化验k＋1次。‎ 假设此次普查中每个人的血样化验呈阳性的概率为p，且这些人之间的试验反应相 互独立。‎ ‎(1)设方案②中，某组k个人的每个人的血化验次数为X，求X的分布列；‎ ‎(2)设p＝0.1，试比较方案②中，k分别取2，3，4时，各需化验的平均总次数；并指出在这三种分组情况下，相比方案①，化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)‎ ‎(二)选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22.[选修4－4：坐标系与参数方程](本小题满分10分)‎ 心形线是由一个圆上的一个定点，当该圆在绕着与其相切且半径相同的另外一个圆周上滚动时，这个定点的轨迹，因其形状像心形而得名在极坐标系Ox中，方程ρ＝a(1－sinθ)(a>0)表示的曲线C1就是一条心形线，如图，以极轴Ox所在的直线为x轴，极点O为坐标原点的直角坐标系xOy中，已知曲线C2的参数方程为(t为参数)。‎ ‎(1)求曲线C2的极坐标方程；‎ ‎(2)若曲线C1与C2相交于A、O、B三点，求线段AB的长。‎ ‎23.[选修4－5：不等式选讲](本小题满分10分)‎ 已知函数f(x)＝|x＋a|＋|x－2|，a∈R。‎ ‎(1)当a＝1时，求不等式f(x)≥7的解集；‎ ‎(2)若f(x)≤|x－4|＋|x＋2a|的解集包含[0，2]。求a的取值范围。‎