2016届高考数学（理）大一轮复习达标训练试题：课时跟踪检测(四十二)　空间几何体的结构特征及三视图与直观图 5页

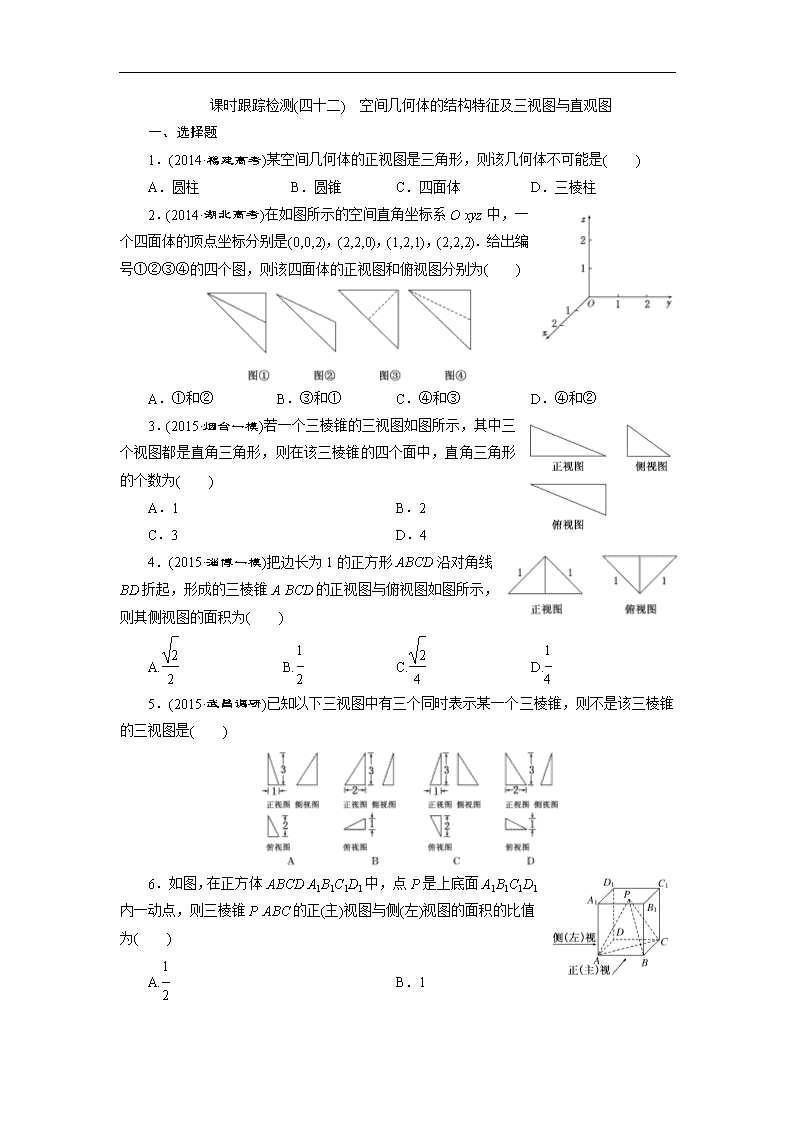
课时跟踪检测(四十二)　空间几何体的结构特征及三视图与直观图 一、选择题 ‎1．(2014·福建高考)某空间几何体的正视图是三角形，则该几何体不可能是(　　)‎ A．圆柱　　　 B．圆锥　　　 C．四面体　　　 D．三棱柱 ‎2．(2014·湖北高考)在如图所示的空间直角坐标系Oxyz中，一个四面体的顶点坐标分别是(0,0,2)，(2,2,0)，(1,2,1)，(2,2,2)．给出编号①②③④的四个图，则该四面体的正视图和俯视图分别为(　　)‎ A．①和② B．③和① C．④和③ D．④和②‎ ‎3．(2015·烟台一模)若一个三棱锥的三视图如图所示，其中三个视图都是直角三角形，则在该三棱锥的四个面中，直角三角形的个数为(　　)‎ A．1　　　　 B．2‎ C．3　　　　 D．4‎ ‎4．(2015·淄博一模)把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥ABCD的正视图与俯视图如图所示，则其侧视图的面积为(　　)‎ A. B. C. D. ‎5．(2015·武昌调研)已知以下三视图中有三个同时表示某一个三棱锥，则不是该三棱锥的三视图是(　　)‎ ‎6．如图，在正方体ABCDA1B‎1C1D1中，点P是上底面A1B‎1C1D1内一动点，则三棱锥PABC的正(主)视图与侧(左)视图的面积的比值为(　　)‎ A. B．1‎ C．2 D．不确定，与点P的位置有关 二、填空题 ‎7．(2015·西城区期末)已知一个正三棱柱的所有棱长均相等，其侧(左)视图如图所示，那么此三棱柱正(主)视图的面积为________．‎ ‎8．如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′＝6，O′C′＝2，则原图形OABC的面积为________．‎ ‎9．(2015·武邑一模)某几何体的一条棱长为，在该几何体的正视图中，这条棱的投影是长为的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a＋b的最大值为________．‎ ‎10．给出下列命题：①在正方体上任意选择4个不共面的顶点，它们可能是正四面体的4个顶点；②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；③若有两个侧面垂直于底面，则该四棱柱为直四棱柱．其中正确命题的序号是________．‎ 三、解答题 ‎11．已知：图①是截去一个角的长方体，试按图示的方向画出其三视图；图②是某几何体的三视图，试说明该几何体的构成．‎ ‎12．如图，在四棱锥PABCD中，底面为正方形，PC与底面ABCD 垂直，下图为该四棱锥的正视图和侧视图，它们是腰长为‎6 cm的全等的等腰直角三角形．‎ ‎(1)根据图所给的正视图、侧视图，画出相应的俯视图，并求出该俯视图的面积；‎ ‎(2)求PA.‎ 答案 ‎1．选A　圆柱的正视图是矩形，则该几何体不可能是圆柱．‎ ‎2.选D　在空间直角坐标系Oxyz中作出棱长为2的正方体，在该正方体中作出四面体，如图所示，由图可知，该四面体的正视图为④，俯视图为②.选D.‎ ‎3．选D　观察三视图，可得直观图如图所示．该三棱锥ABCD的底面BCD是直角三角形，AB⊥平面BCD，CD⊥BC，侧面ABC，ABD是直角三角形；由CD⊥BC，CD⊥AB，知CD⊥平面ABC，CD⊥AC，侧面ACD也是直角三角形，故选D.‎ ‎4．选D　由正视图与俯视图可得三棱锥ABCD的一个侧面与底面垂直，其侧视图是直角三角形，且直角边长均为，所以侧视图的面积为S＝××＝，选D.‎ ‎5．选D　易知该三棱锥的底面是直角边分别为1和2的直角三角形，注意到侧视图是从左往右看得到的图形，结合B、D选项知，D选项中侧视图方向错误，故选D.‎ ‎6．选B　 如题图所示，设正方体的棱长为a，则三棱锥PABC的正(主)视图与侧(左)‎ 视图都是三角形，且面积都是a2，故选B.‎ ‎7．解析：由正三棱柱三视图还原直观图可得正(主)视图是一个矩形，其中一边的长是侧(左)视图中三角形的高，另一边是棱长．因为侧(左)视图中三角形的边长长为2，所以高为，所以正视图的面积为2.‎ 答案：2 ‎8．解析：由题意知原图形OABC是平行四边形，且OA＝BC＝6，设平行四边形OABC的高为OE，则OE××＝O′C′，‎ ‎∵O′C′＝2，∴OE＝4，‎ ‎∴S▱OABC＝6×4＝24.‎ 答案：24 ‎9．解析：本题构造长方体，体对角线长为，其在侧视图中为侧面对角线a，在俯视图中为底面对角线b，设长方体底面宽为1，则b2－1＋a2－1＝6，即a2＋b2＝8，利用不等式2≤＝4，则a＋b≤4.‎ 答案：4‎ ‎10．解析：①正确，正四面体是每个面都是等边三角形的四面体，如正方体ABCD A1B‎1C1D1中的四面体A CB1D1；②错误，反例如图所示，底面△ABC为等边三角形，可令AB＝VB＝VC＝BC＝AC，则△VBC为等边三角形，△VAB和△VCA均为等腰三角形，但不能判定其为正三棱锥；③错误，必须是相邻的两个侧面．‎ 答案：①‎ ‎11．解：图①几何体的三视图为：‎ 图②所示的几何体是上面为正六棱柱，下面为倒立的正六棱锥的组合体．‎ ‎12．解：(1)该四棱锥的俯视图为(内含对角线)边长为‎6 cm的正方形，如图，其面积为‎36 cm2.‎ ‎(2)由侧视图可求得PD＝＝＝6.‎ 由正视图可知AD＝6，且AD⊥PD，所以在Rt△APD中，‎ PA＝＝＝‎6 cm.‎