课时20+平行关系-2019年高考数学（文）单元滚动精准测试卷 8页

模拟训练（分值：60分 建议用时：30分钟）‎ ‎1.若平面α∥平面β，直线a∥平面α，点B∈β,则在 平面β内且过B点的所有直线中( ) ‎ ‎ A.不一定存在与a平行的直线 ‎ B.只有两条与a平行的直线 ‎ C.存在无数条与a平行的直线 D.存在唯一与a平行的直线 ‎【答案】A.‎ ‎2.平面α∥平面β的一个充分条件是(　　)‎ A．存在一条直线a，a∥α，a∥β B．存在一条直线a，a⊂α，a∥β C．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α D．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α ‎【答案】D ‎【解析】A、B、C中α与β都有可能相交．‎ ‎3.下列命题中正确的个数是(　　)‎ ‎①若直线a不在α内，则a∥α；‎ ‎②若直线l上有无数个点不在平面α内，则l∥α；‎ ‎③若直线l与平面α平行，则l与α内的任意一条直线都平行；‎ ‎④如果两条平行线中的一条与一个平面平行，那么另一条也与这个平面平行；‎ ‎⑤若l与平面α平行，则l与α内任何一条直线都没有公共点；‎ ‎⑥平行于同一平面的两直线可以相交．‎ A．1　　　　　　　　　　 B．2‎ C．3 D．4‎ ‎【答案】B ‎【解析】a∩α＝A时，a不在α内，∴①错；直线l与α相交时，l上有无数个点不在α内，故②错；l∥α时，α内的直线与l平行或异面，故③错；a∥b，b∥α时，a∥α或a⊂α，故④错；l∥α，则l与α无公共点，∴l与α内任何一条直线都无公共点，⑤正确；如图，长方体中，A1C1与B1D1都与平面ABCD平行，∴⑥正确．‎ ‎4．设m、n、l是三条不同的直线，α、β、γ是三个不同的平面，则下列命题中的真命题是(　　)‎ A．若m、n与l所成的角相等，则m∥n B．若γ与α、β所成的角相等，则α∥β C．若m、n与α所成的角相等，则m∥n D．若α∥β，m⊂α，则m∥β ‎【答案】D ‎5．若直线a⊥b，且直线a∥平面α，则直线b与平面α的位置关系是(　　)‎ A．b⊂α B．b∥α C．b⊂α或b∥α D．b与α相交或b∥α或b⊂α ‎【答案】D ‎【解析】由a⊥b，a∥平面α，可知b与α或平行或相交或b⊂α. 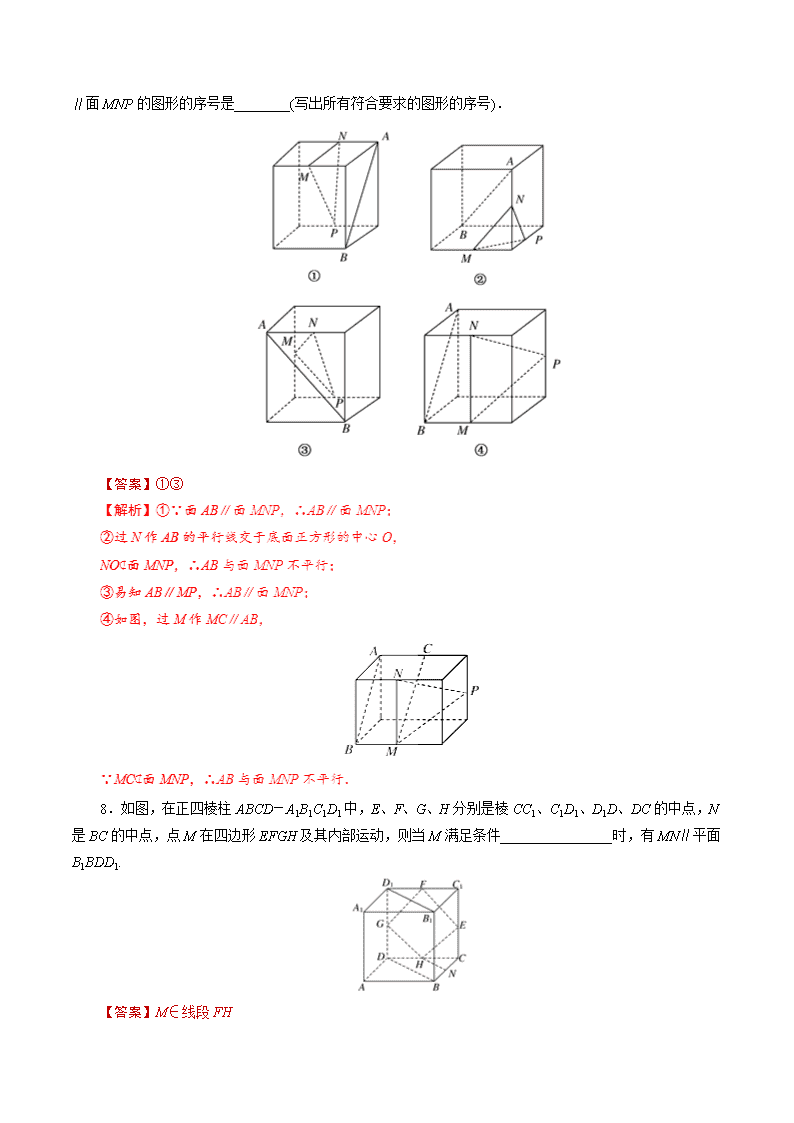学……&科网 ‎6．已知m、n是不同的直线，α、β是不重合的平面，给出下列命题：‎ ‎①若m∥α，则m平行于平面α内的无数条直线；‎ ‎②若α∥β，m⊂α，n⊂β，则m∥n；‎ ‎③若m⊥α，n⊥β，m∥n，则α∥β；‎ ‎④若α∥β，m∥α，则m∥β.‎ 其中，真命题的序号是________(写出所有真命题的序号)．‎ ‎【答案】①③‎ ‎【解析】由线面平行定义及性质知①正确．②中若m⊂α，n⊂β，α∥β，‎ 则m、n可能平行，也可能异面，故②错，‎ ‎③中由⇒⇒α∥β知③正确．‎ ‎④中由α∥β，m∥α可得，m∥β或m⊂β，故④错．‎ ‎7．下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB ‎∥面MNP的图形的序号是________(写出所有符合要求的图形的序号)．‎ ‎【答案】①③‎ ‎8．如图，在正四棱柱ABCD－A1B1C1D1中，E、F、G、H分别是棱CC1、C1D1、D1D、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则当M满足条件________________时，有MN∥平面B1BDD1.‎ ‎【答案】M∈线段FH ‎【解析】当M点满足在线段FH上有MN∥面B1BDD1.‎ ‎【失分点分析】在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误.‎ ‎9. 如图，在正方体ABCD—A1B1C1D1中，点N在BD上，点M在B1C上，且CM＝DN，求证：MN∥平面AA1B1B. ‎ 分析一：若能证明MN平行于平面AA1B1B中的一条直线，则依线面平行判定定理，MN∥平面AA1B1B.于是有以下两种添辅助线的方法．‎ ‎【证明】：证法一：如右图，作ME∥BC，交BB1于E；作NF∥AD，交AB于F.连结EF，则EF⊂平面AA1B1B.‎ ‎∴MEFN为平行四边形．‎ ‎∴MN∥EF.‎ 分析二：若过MN能作一个平面与平面AA1B1B平行，则由面面平行的性质定理，可得MN与平面AA1B1B平行．‎ 证法三：如图，作MP∥BB1，交BC于点P，连结NP.‎ ‎∵MP∥BB1，‎ ‎∴＝.‎ ‎∵BD＝B1C，DN＝CM，‎ ‎∴B1M＝BN.‎ ‎【规律总结】证明直线l与平面α平行，通常有以下两个途径：‎ ‎(1)通过线线平行来证明，即证明该直线l平行于平面α内的一条直线；‎ ‎(2)通过面面平行来证明，即证明过该直线l的一个平面平行于平面α.‎ ‎10．如图，棱柱ABCD－A1B1C1D1的底面ABCD为菱形，平面AA1C1C⊥平面ABCD.‎ ‎(1)证明：BD⊥AA1；‎ ‎(2)证明：平面AB1C∥平面DA1C1； ‎ ‎(3)在直线CC1上是否存在点P，使BP∥平面DA1C1？若存在，求出点P的位置；若不存在，说明理由．‎ ‎【解析】(1)证明：连接BD，‎ ‎∵平面ABCD为菱形，‎ ‎∴BD⊥AC，‎ 由于平面AA1C1C⊥平面ABCD，‎ 则BD⊥平面AA1C1C，‎ 又A1A⊂平面AA1C1C，‎ 故BD⊥AA1.‎ ‎(2)证明：由棱柱ABCD－A1B1C1D1的性质知AB1∥DC1，A1D∥B1C，‎ AB1∩B1C＝B1，A1D∩DC1＝D，‎ 由面面平行的判定定理推论知：平面AB1C∥平面DA1C1.‎ ‎(3)存在这样的点P满足题意．‎ ‎∵A1B1綊AB綊DC，‎ ‎ [知识拓展]证明面面平行的方法有：‎ ‎（1）面面平行的定义；‎ ‎（2）面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行；‎ ‎（3）利用垂直于同一条直线的两个平面平行；‎ ‎（4）两个平面同时平行于第三个平面，那么这两个平面平行；‎ ‎（5）利用“线线平行”、“线面平行”、“面面平行”的相互转化.‎ ‎[新题训练] （分值：10分 建议用时：10分钟）‎ ‎11.（5分）已知平面α∥平面β，P是α、β外一点，过点P 的直线m与α、β分别交于A、C，过点P的直线n 与α、β分别交于B、D且PA=6,AC=9，PD=8，则BD的长为 .‎ ‎【答案】‎ ‎【解析】根据题意可出现以下如图两种情况：‎ 可求出BD的长分别为 .‎ ‎12.（5分）如图，在三棱柱ABC—A′B′C′中，点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点，G为△ABC的重心．从K、H、G、B′中取一点作为P，使得该棱柱恰有2条棱与平面PEF平行，则P为 (　　)‎ A．K ‎ B．H C．G ‎ D． B′‎ ‎【答案】C ‎ ‎