2021届课标版高考理科数学大一轮复习课件：4-3　三角函数的图象和性质（讲解部分） 20页

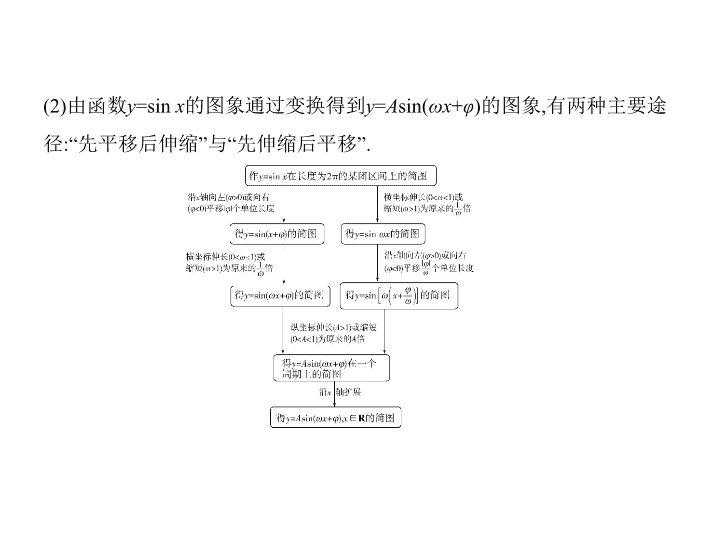
考点一    三角函数的图象及其变换 考点清单 考向基础 　　1.“五点法”作图原理:在确定正弦函数 y =sin x 在[0,2π]上的图象的形 状时,起关键作用的五个点是(0,0)、   、(π,0)、   、(2π,0). 2.作 y = A sin( ωx + φ )( ω >0)的图象主要有以下两种方法: (1)五点法 用五点法作 y = A sin( ωx + φ )的简图,主要是通过变量代换,设 z = ωx + φ ,由 z 取 0,   ,π,   ,2π 来求出相应的 x ,通过列表计算得出五点坐标,描点后得出图象. (2)由函数 y =sin x 的图象通过变换得到 y = A sin( ωx + φ )的图象,有两种主要途 径:“先平移后伸缩”与“先伸缩后平移”. 联系:上述两种变换方法都是针对 x 而言的,即 x 本身加减多少,而不是 ωx 加 减多少. 区别:先相位变换再周期变换(伸缩变换),平移的量是| φ |个单位;而先周期变 换(伸缩变换)再相位变换,平移的量是   ( ω >0)个单位.原因在于相位变换 和周期变换都是针对 x 而言的. 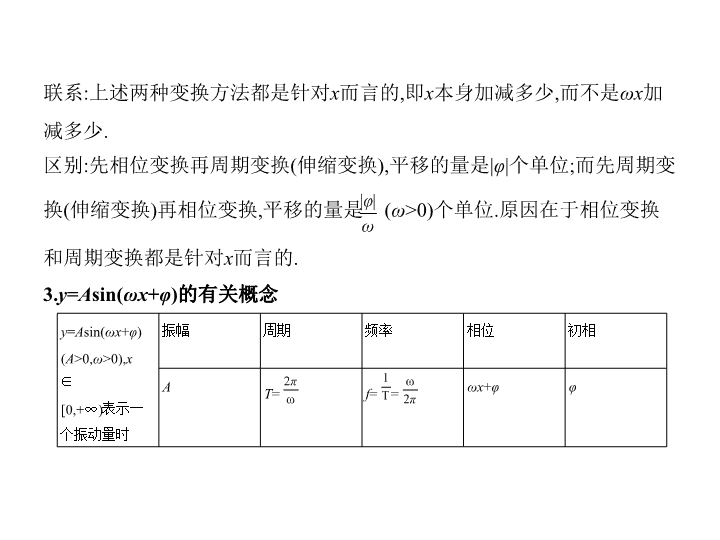3. y = A sin( ωx + φ )的有关概念 y = A sin( ωx + φ ) ( A >0, ω >0), x ∈ [0,+ ∞ )表示一 个振动量时 振幅 周期 频率 相位 初相 A T =   f =   =   ωx + φ φ 考向突破 考向    三角函数的图象及其变换 例     (2019安徽蚌埠第二次教学质量检查,9)将函数 f ( x )=sin x +cos x 的图象 上各点的横坐标缩小为原来的   ,纵坐标不变,再将函数图象向左平移   个 单位后,所得图象对应的函数( g ( x ))的解析式为(　　) A. g ( x )=   sin   　　　　     B. g ( x )=   sin   C. g ( x )=   sin   　　　　     D. g ( x )=   sin   解析      f ( x )=sin x +cos x =   sin   的图象   y =   sin   的图象   g ( x )=   sin   =   sin 的图象.故选B. 答案     B 考点二    三角函数的性质及其应用 考向基础 函数 性质　     y =sin x y =cos x y =tan x 定义域 R R   x   x ≠ k π+   , k ∈Z   图象       值域 [-1,1] [-1,1] R 对称性 对称轴: x = k π+   ( k ∈Z) ; 对称中心: ( k π,0)( k ∈Z) 对称轴: x = k π( k ∈Z) ; 对称中心:   ( k ∈Z) 对称中心:   ( k ∈Z) 周期 2π 2π π 单调性 单调增区间:   2 k π-   ,2 k π+     ( k ∈Z) ; 单调减区间: 2 k π+   , 2 k π+   ( k ∈Z) 单调增区间: [2 k π-π,2 k π]( k ∈Z) ; 单调减区间: [2 k π,2 k π+π]( k ∈Z) 单调增区间:   k π-   , k π+     ( k ∈Z) 奇偶性 奇 偶 奇 考向突破 考向一    三角函数的单调性 例1 　已知函数 f ( x )=sin ωx +cos ωx ( ω >0), x ∈R.若函数 f ( x )在区间(- ω , ω )内单 调递增,且函数 y = f ( x )的图象关于直线 x = ω 对称,则 ω 的值为 　　　     . 解题导引   解析 　由已知得 f ( x )=   sin   ,令2 k π-   ≤ ωx +   ≤ 2 k π+   , k ∈Z,由 ω >0, 得   ≤ x ≤   , k ∈Z, 当 k =0时, f ( x )的单调递增区间为   , 所以(- ω , ω ) ⊆   , 所以   所以0< ω ≤   , 又 y = f ( x )的图象关于直线 x = ω 对称,所以 ω 2 +   = k π+   , k ∈Z, 解得 ω 2 = k π+   , k ∈Z, 又0< ω ≤   ,所以 ω =   . 答案        考向二    三角函数的对称性、奇偶性和周期性 例2     (2019湖南衡阳高中毕业班联考(二),4)将函数 f ( x )的图象向右平移   个单位长度,再将所得函数图象上的所有点的横坐标缩短到原来的   ,得到 函数 g ( x )= A sin( ωx + φ )   的图象.已知函数 g ( x )的部分图象如 图所示,则函数 f ( x )   (　　)   A.的最小正周期为   π,最大值为2 B.的最小正周期为π,图象关于点   中心对称 C.的最小正周期为   π,图象关于直线 x =   对称 D.的最小正周期为π,在区间   上单调递减 解析 　对于 g ( x ),由题图可知, A =2, T =4   =   ,∴ ω =   =3.则 g ( x )= 2sin(3 x + φ ), 又由 g   =2可得 φ =-   +2 k π, k ∈Z, 又| φ |<   ,∴ φ =-   . ∴ g ( x )=2sin   ,∴ f ( x )=2sin   . ∴ f ( x )的最小正周期为π,选项A,C错误. 对于选项B,令2 x +   = k π( k ∈Z),所以 x =   -   , k ∈Z,所以函数 f ( x )图象的对称 中心为   ( k ∈Z),所以选项B是错误的.当 x ∈   时,2 x +   ∈   ,所以 f ( x )在   上是减函数,所以选项D正确.故选D. 答案     D 方法1      由三角函数图象确定函数解析式的方法 求函数 y = A sin( ωx + φ )+ B ( A >0, ω >0)解析式的方法与步骤 (1)求 A 、 B ,确定函数的最大值 M 和最小值 m ,则 A =   , B =   . (2) ω 由周期得到, ω =   ,确定周期时可利用以下结论: a.函数图象的相邻两条对称轴之间的距离为函数的半个周期; b.函数图象的相邻两个对称中心间的距离也为函数的半个周期; c.一条对称轴与其相邻的一个对称中心间的距离为函数的   个周期(借助 图象很好理解、记忆). 方法技巧 (3)利用峰点、谷点或零点列出关于 φ 的方程,结合 φ 的范围解得 φ 的值,所列 方程如下: 峰点: ωx + φ =   +2 k π( k ∈Z); 谷点: ωx + φ =-   +2 k π( k ∈Z). 利用零点时,要区分该零点是升零点,还是降零点. 升零点(图象上升时与 x 轴的交点的横坐标): ωx + φ =2 k π( k ∈Z); 降零点(图象下降时与 x 轴的交点的横坐标): ωx + φ =π+2 k π( k ∈Z). 例 1 (2019河南郑州三模,9)已知函数 f ( x )= A sin( ωx + φ )   的部分 图象如图所示,则使 f ( a + x )- f ( a - x )=0成立的 a 的最小正值为   (　　) A.   　　　　　　　    B.   　　　　     C.   　　　　　　　    D.   解析 　由题图可知, A =2,故 f ( x )=2sin( ωx + φ ), ∵ f (0)=2sin φ =1,∴sin φ =   ,∵| φ |<   , ∴ φ =   ,故 f ( x )=2sin   ,结合题图及五点作图法可知, ω ×   +   =2π,∴ ω =2,故 f ( x )=2sin   ,其图象的对称轴为直线 x =   +   k π, k ∈Z.∵ f ( a + x )- f ( a - x )=0成立,∴ f ( a + x )= f ( a - x ),即 f ( x )的图象关于直线 x = a 对称,所以满足条件的 a 的最小正值为   .故选B. 答案     B 方法2     三角函数的性质及其应用 1.三角函数的单调性 (1)求函数的单调区间应遵循简单化原则,将解析式进行化简,并注意复合 函数单调性规律“同增异减”. (2)求形如 y = A sin( ωx + φ )或 y = A cos( ωx + φ )(其中 ω >0)的单调区间时,要视“ ωx + φ ”为一个整体,通过解不等式求解.但如果 ω <0,那么一定先借助诱导公 式将 ω 化为正数. (3)已知三角函数的单调区间求参数,先求出函数的单调区间,然后利用集 合间的关系求解. 2.三角函数的奇偶性 对于 y = A sin( ωx + φ ),若为奇函数,则 φ = k π( k ∈Z);若为偶函数,则 φ =   + k π( k ∈Z).对于 y = A cos( ωx + φ ),若为奇函数,则 φ =   + k π( k ∈Z);若为偶函数,则 φ = k π ( k ∈Z).对于 y = A tan( ωx + φ ),若为奇函数,则 φ =   ( k ∈Z). 3.三角函数的周期性 求三角函数的最小正周期,一般先通过恒等变换化为 y = A sin( ωx + φ )或 y = A cos( ωx + φ )或 y = A tan( ωx + φ )( A , ω , φ 为常数, A ≠ 0, ω ≠ 0)的形式,再应用公式 T =   (正弦、余弦型)或 T =   (正切型)求解. 4.三角函数的对称性 函数 f ( x )= A sin( ωx + φ )( A , ω , φ 为常数, A ≠ 0, ω ≠ 0)图象的对称轴一定经过图象 的最高点或最低点,对称中心的横坐标一定是函数的零点,因此在判断直线 x = x 0 或点( x 0 ,0)是不是函数图象的对称轴或对称中心时,可通过检验 f ( x 0 )的 值进行. 例2     (2018河北五个一联盟4月联考,10)已知函数 f ( x )=1+2cos x cos( x +3 φ )是 偶函数,其中 φ ∈   ,则下列关于函数 g ( x )=cos(2 x - φ )的描述正确的是   (　　) A. g ( x )在区间   上的最小值为-1 B. g ( x )的图象可由函数 f ( x )的图象向上平移2个单位长度,再向右平移   个单 位长度得到 C. g ( x )的图象的一个对称中心是   D. g ( x )的一个单调递减区间是   解析 　∵函数 f ( x )=1+2cos x cos( x +3 φ )是偶函数, y =1, y =2cos x 都是偶函数, ∴ y =cos( x +3 φ )是偶函数,∴3 φ = k π, k ∈Z,∴ φ =   , k ∈Z,又0< φ <   ,∴ φ =   ,∴ g ( x ) =cos   .当-   ≤ x ≤   时,-   ≤ 2 x -   ≤   ,cos   ∈[0,1],故A错误; f ( x ) =1+2cos x cos( x +π)=1-2cos 2 x =-cos 2 x ,显然B错误;当 x =-   时, g ( x )=cos   = 0,故C正确;由2 k π ≤ 2 x -   ≤ 2 k π+π( k ∈Z)得 k π+   ≤ x ≤ k π+   π( k ∈Z),当 k =0 时, x ∈   ,即 g ( x )在   上单调递减,故D错误. 答案     C