高中数学选修2-1公开课课件3_1_1空间向量及其加减运算 20页

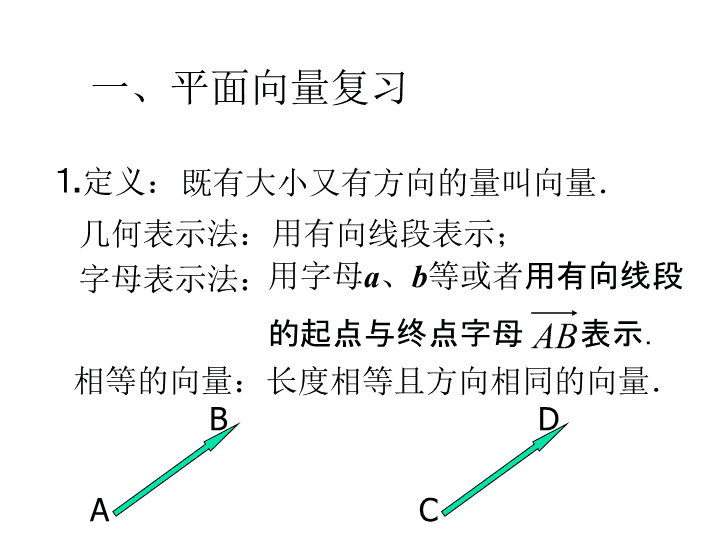
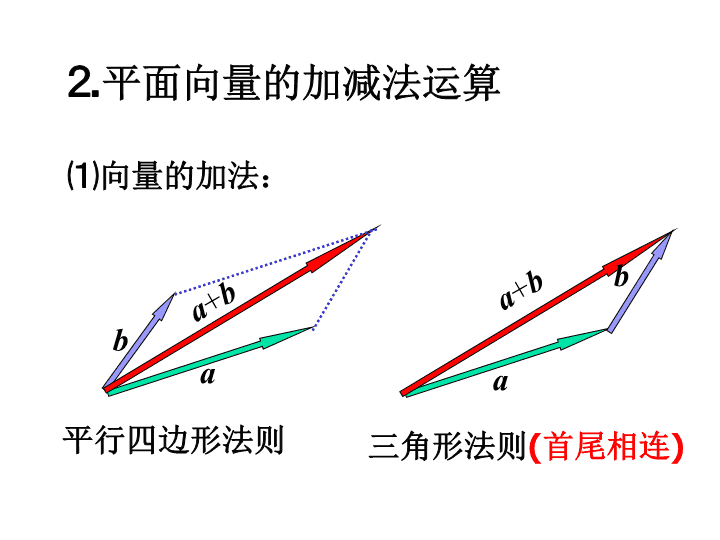
3.1.1 空间向量及其加减运算 一、平面向量复习 ⒈ 定义： 既有大小又有方向的量叫向量． 几何表示法： 用有向线段表示； 字母表示法： 用字母 a 、 b 等或者 用有向线段 的起点与终点字母 表示． 相等的向量： 长度相等且方向相同的向量． A B C D ⒉ 平面向量的加减法运算 ⑴ 向量的加法： a b a + b 平行四边形法则 a b a + b 三角形法则 (首尾相连) ⑵ 向量的减法 a b a - b 三角形法则 减向量 终点指向 被减向量 终点 ⒊ 平面向量的加法运算律 加法交换律： a ＋ b ＝ b ＋ a 加法结合律： ( a ＋ b ) ＋ c ＝ a ＋ ( b ＋ c ) 推广 ⑴ 首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量．即： ⑵ 首尾相接的若干向量构成一个封闭图形，则它们的和为零向量．即： 二、空间向量及其加减运算 ⒈ 空间向量： 空间中具有 大小 和 方向 的量叫做向量． ⑴ 定义： ⑵ 表示方法 ： ① 空间向量的表示方法和平面向量一样； ③ 空间任意两个向量都可以用同一平面　 　内的两条有向线段表示． ② 同向且等长的有向线段表示同一向量或 　相等的向量； 2. 空间向量的加法、减法向量 a + b a b A B b C O a - b ⒊ 空间向量加法运算律 ⑴ 加法交换律： a + b = b + a ； ⑵ 加法结合律： ( a + b ) + c = a + ( b + c ) ； a b c a + b + c a b c a + b + c a + b b + c 对空间向量的加法、减法的说明 ⒈ 空间向量的运算就是平面向量运算的推广． ⒉ 两个向量相加的平行四边形法则在空间仍 　然成立． ⒊ 空间向量的加法运算可以推广至若干个向 　量相加． 推广 ⑴ 首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量．即： ⑵ 首尾相接的若干向量构成一个封闭图形，则它们的和为零向量．即： 例1、给出以下命题： （1）两个空间向量相等，则它们的起点、终点相同； （2）若空间向量 满足 ，则 ； （3）在正方体 中，必有 ； （4）若空间向量 满足 ，则 ； （5）空间中任意两个单位向量必相等。 其中不正确命题的个数是（ ） A.1 B.2 C.3 D.4 C 变式： 如图所示，长方体中， AD=2，AA 1 =1，AB=3。 （1） 是写出与 相等的所有向量； （2）写出与向量 的相反向量。 平行六面体： 平行四边形 ABCD 平移向量 a 到 A 1 B 1 C 1 D 1 的轨迹所形成的几何体，叫做平行六面体。 A B C D A 1 B 1 C 1 D 1 A 1 D 1 C 1 B 1 B A C D 记作 ABCD—A 1 B 1 C 1 D 1， 它的六个面都是平行四边形，每个面的边叫做平行六面体的棱。 a A B C D A ’ B ’ C ’ D ’ 例 2 解： A B C D A ’ B ’ C ’ D ’ 始点相同的三个不共面向量之和，等于以这三个向量 为棱的平行六面体的以公共始点为始点的对角线所示向量 例3、在如图所示的平行六面体中， 求证： A B C D A ’ B ’ C ’ D ’ 变式： 已知平行六面体 则下列四式中： 其中正确的是 。 例4、如图所示，在正方体 中，下列各式中运算的结果为向量 的共有（ ） A.1 B.2 C.3 D.4 变式： 平面向量 概念 加法 减法 数乘 运算 运 算 律 定义 表示法 相等向量 减法 : 三角形法则 加法 : 三角形法则或 平行四边形法则 空间向量 具有大小和方向的量 加法交换律 加法结合律 小结 加法交换律 加法结合律 类比、数形结合