辽宁省辽南协作校2020届高三下学期模拟考试模拟考试数学理试题 13页

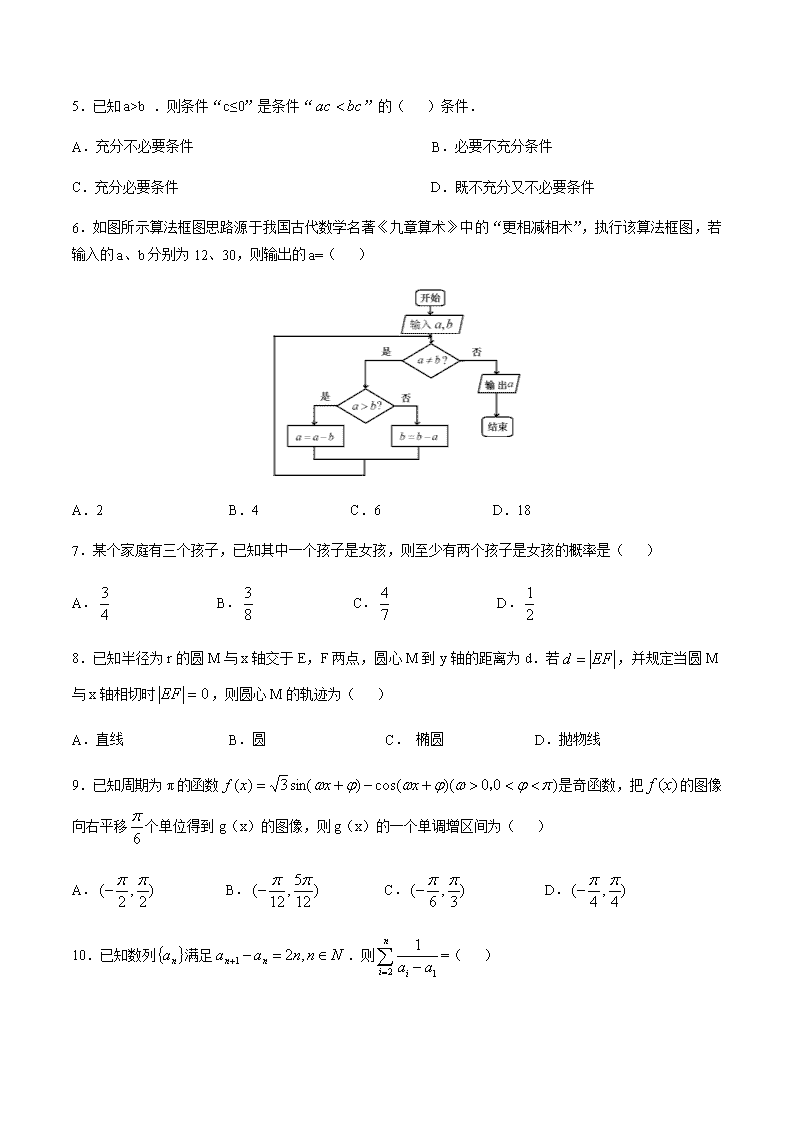
姓 名： 考生考号： ‎ ‎2019—2020学年度下学期高三第二次模拟考试试试题 数学（理科）‎ 时间：120分钟 试卷满分：150分 本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分 第1卷 一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的 ‎1．已知，，则AB=（ ）‎ A． B．R C． D．‎ ‎2．已知复数．则=（ ）‎ A． B．‎1 C．0 D．2‎ ‎3．已知某地区中小学生人数和近视情况分别如图甲和图乙所示．为了了解该地区中小学生的近视形成原因用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为（ ）‎ A．100，40 B．100，‎20 C．200，40 D．200，20‎ ‎4设是直线，是两个不同的平面，下列命题中正确的是（ ）‎ A．若，，则 B．若， ，则 C．若，，则 D．若，，则 ‎5．已知a>b ．则条件“c≤‎0”‎是条件“”的（ ）条件．‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充分必要条件 D．既不充分又不必要条件 ‎6．如图所示算法框图思路源于我国古代数学名著《九章算术》中的“更相减相术”，执行该算法框图，若输入的a、b分别为12、30，则输出的a=（ ）‎ A．2 B．‎4 C．6 D．18‎ ‎7．某个家庭有三个孩子，已知其中一个孩子是女孩，则至少有两个孩子是女孩的概率是（ ）‎ A． B． C． D．‎ ‎8．已知半径为r的圆M与x轴交于E，F两点，圆心M到y轴的距离为d．若，并规定当圆M与x轴相切时，则圆心M的轨迹为（ ）‎ A．直线 B．圆 C． 椭圆 D．抛物线 ‎9．已知周期为π的函数是奇函数，把的图像向右平移个单位得到g（x）的图像，则g（x）的一个单调增区间为（ ）‎ A． B． C． D．‎ ‎10．已知数列满足．则=（ ）‎ A． B． C．n（n-1） D．‎ ‎11．在直角坐标系xOy中，F是椭圆C：的左焦点，A，B分别为左、右顶点，过点F作x轴的垂线交椭圆C于P，Q两点，连接PB交y轴于点E ，连接AE交PQ于点M ，若M是线段PF的中点，则椭圆C的离心率为（ ）‎ A． B． C． D．‎ ‎12．已知函数f（x）满足，．当x>0时，下列说法：‎ ‎① ②只有一个零点 ‎③有两个零点 ④有一个极大值 其中正确的是（ ）‎ A．①③ B．②③ C．①④ D．②④‎ 第Ⅱ卷 本卷包括必考题和选考题两部分，第13-21题为必考题，每个试题考生都必须作答，第22-23题为选考题，考生根据要求作答。‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．已知函数（a＞0且a≠1）的图像恒过定点P，且点P在函数的图象上，则 ．‎ ‎14．已知数列为等差数列，a1，a2，a5成公比不为1的等比数列，且a9=4，则公差d= ．‎ ‎15．已知平面向量与的夹角60°，且，．若平面向量满足，则 ．‎ ‎16．已知三棱锥P—ABC的四个顶点在球O的球面上，PA=PB= PC，△ABC是边长为2的正三角形，E 为PA中点，BE=PB，则球O的体积为 ．‎ 三、解答题 ‎17．（本题满分12分）‎ 已知△ABC的内角A、B、C所对的边分别为a 、b、c，且．‎ ‎（1）求角A的值．‎ ‎（2）若△ABC面积为，且b+c=7（b＞c），求a及sin B的值．‎ ‎18．（本题满分12分）‎ 数据的收集和整理在当今社会起到了举足轻重的作用，它用统计的方法来帮助人们分析以往的行为习惯，进而指导人们接下来的行动．‎ 某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员，他收集到了甲、乙两名球员近期5场比赛的传球成功次数，如下表：‎ ‎ 场次 第一场 第二场 第三场 第四场 第五场 甲 ‎28‎ ‎33‎ ‎36‎ ‎38‎ ‎45‎ 乙 ‎39‎ ‎31‎ ‎43‎ ‎39‎ ‎33‎ ‎（1） 根据这两名球员近期5场比赛的传球成功次数，完成下面茎叶图（茎表示十位，叶表示个位）；分别在平面直角坐标系中画出两名球员的传球成功次数的散点图；‎ ‎（2）求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差；‎ ‎（3）主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平，同时根据多场比赛的数据也可以分析出球员的状态和潜力．你认为主教练应选哪位球员?并说明理由。‎ ‎19．（本题满分12分）‎ 已知矩形ABCD，AB=2BC，E为DC中点，将△BCD治BD折起，连结AC 、AE、 BE．‎ ‎（1）当AE⊥BC时，求证： AD⊥AC；‎ ‎（2）当时，求二面角C—BD—A的余弦值．‎ ‎20．（本题满分12分）‎ 已知函数．‎ ‎（1）若a=3 ．证明函数有且仅有两个零点：‎ ‎（2）若函数存在两个零点，证明：．‎ ‎21．（本题满分12分）‎ 已知点M是抛物线C：的准线与x轴的交点，点P是抛物线C1上的动点，点A、B在y轴上，△APB的内切圆为圆C2：， C2为圆心，且，其中O为坐标原点．‎ ‎（1）求抛物线C1的标准方程；‎ ‎（2）求△APB面积的最小值．‎ 请考生在22—23题中任选一题作答。如果多做，则按所做的第一题计分。作答时请写（涂）清题号。‎ ‎22．（本题满分10分）选修4—4：坐标系与参数方程 在直角坐标系xOy中，直线的参数方程为（t为参数），圆C的参数方程为（为参数）‎ ‎（1）求和C的普通方程；‎ ‎（2）将向左平移m（m>0）个单位后，得到直线，若圆C上只有一个点到的距离为1，求m的值．‎ ‎23．（本题满分10分）选修4—5：不等式选讲 设函数．‎ ‎（1）当a=1时，求不等式f（x）