2020年高考数学(理)二轮复习讲练测 专题09 立体几何（测）（解析版） 14页

专题09 立体几何(测)‎ ‎【满分：100分 时间：90分钟】‎ 一、选择题(12*5=60分)‎ ‎1．下列命题正确的是( )‎ A、若两条直线和同一个平面所成的角相等，则这两条直线平行 B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 D、若两个平面都垂直于第三个平面，则这两个平面平行 ‎【答案】C ‎【解析】若两条直线和同一平面所成角相等，这两条直线可能平行，也可能为异面直线，也可能相交，所以A错；一个平面不在同一条直线的三点到另一个平面的距离相等，则这两个平面平行，故B错；若两个平面垂直同一个平面两平面可以平行，也可以垂直；故D错；故选项C正确.‎ ‎2． 设是直线，α，β是两个不同的平面( )‎ A. 若∥α，∥β，则α∥β B. 若∥α，⊥β，则α⊥β C. 若α⊥β，⊥α，则⊥β D. 若α⊥β, ∥α，则⊥β ‎【答案】B ‎【解析】利用排除法可得选项B是正确的，∵∥a，⊥β，则a⊥β．如选项A：∥a，∥β时，a⊥β或a∥β；选项C：若a⊥β，⊥a，∥β或；选项D：若若a⊥β, ⊥a，∥β或⊥β．‎ ‎3． 如图所示，ABCDA1B‎1C1D1是长方体，O是B1D1的中点，直线A‎1C交平面AB1D1于点M，则下列结论正确的是(　　)‎ A．A，M，O三点共线 B．A，M，O，A1不共面 C．A，M，C，O不共面 D．B，B1，O，M共面 ‎【答案】A ‎【解析】连接A1C1，AC，则A1C1∥AC，∴A1，C1，A，C四点共面，∴A1C⊂平面ACC1A1，∵M∈A1C，‎ ‎∴M∈平面ACC1A1，又M∈平面AB1D1，∴M在平面ACC1A1与平面AB1D1的交线上，同理O在平面ACC1A1与平面AB1D1的交线上．∴A，M，O三点共线．答案：A ‎4． 在梯形中，,,.将梯形绕所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )‎ ‎(A) (B) (C) (D) ‎ ‎【答案】C ‎【解析】。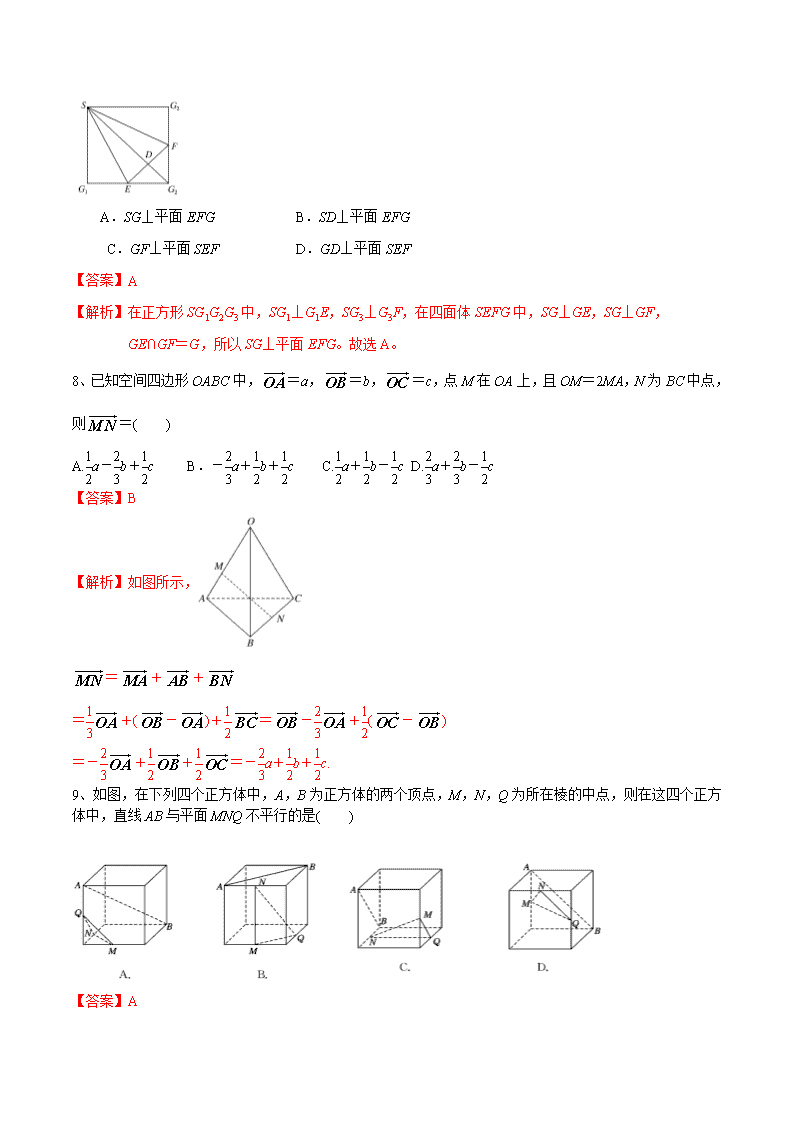‎ ‎5．已知矩形ABCD，AB＝1，BC＝．将ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中( )‎ A．存在某个位置，使得直线AC与直线BD垂直 B．存在某个位置，使得直线AB与直线CD垂直 C．存在某个位置，使得直线AD与直线BC垂直 D．对任意位置，三直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直 ‎【答案】C B ‎【解析】最简单的方法是取一长方形动手按照其要求进行翻着，观察在翻着过程，即可知选项B是正确的．‎ ‎6． 设四面体的六条棱的长分别为1，1，1，1，和，且长为的棱与长为的棱异面，则的取值范围是 ‎(A) (B) (C) (D)‎ ‎【答案】A ‎ ‎【解析】，，，‎ ‎7．如图，在正方形SG‎1G2G3中，E，F分别是G‎1G2，G‎2G3的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个四面体，使G1，G2，G3三点重合，重合后的点记为G，则在四面体S－EFG中必有(　　) ‎ A．SG⊥平面EFG　 B．SD⊥平面EFG ‎ ‎ C．GF⊥平面SEF D．GD⊥平面SEF ‎【答案】A ‎【解析】在正方形SG‎1G2G3中，SG1⊥G1E，SG3⊥G‎3F，在四面体SEFG中，SG⊥GE，SG⊥GF，‎ GE∩GF＝G，所以SG⊥平面EFG。故选A。‎ ‎8、已知空间四边形OABC中，＝a，＝b，＝c，点M在OA上，且OM＝2MA，N为BC中点，则＝(　　)‎ A.a－b＋c B．－a＋b＋c C.a＋b－c D.a＋b－c ‎【答案】B ‎【解析】如图所示，‎ ‎＝＋＋‎ ‎＝＋(－)＋＝－＋(－)‎ ‎＝－＋＋＝－a＋b＋c.‎ ‎9、如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是(　　)‎ ‎【答案】A ‎【解析】对于选项B，如图所示，连接CD，因为AB∥CD，M，Q分别是所在棱的中点，所以MQ∥CD，AB∥MQ，又因为AB⊄平面MQN，MQ⊂平面MQN，所以AB∥平面MQN。同理在选项C、D中都可证得AB∥平面MQN。故选A。‎ ‎10．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有刍甍，下广三丈，袤四丈；上袤二丈，无广；高一丈，问：积几何？”其意思为：“今有底面为矩形的屋脊柱的楔体，下底面宽3丈，长4丈；上棱长2丈，高一丈，问它的体积是多少？”已知1丈为10尺，现将该楔体的三视图给出，其中网格纸上小正方形的边长为1丈，则该楔体的体积为( )‎ A.5500立方尺 B．4000立方尺 C. 6000立方尺 D．5000立方尺 ‎【答案】D ‎【解析】该楔体的直观图如图中的几何体ABC－DEF。‎ 取AB的中点G，CD的中点H，连接FG，GH，HF，则该几何体的体积为四棱锥F－GBCH与三棱柱ADE－GHF的体积之和。又可以将三棱柱ADE－GHF割补成高为EF，底面积为S＝×3×1＝(平方丈)的一个直棱柱，故该楔体的体积V＝×2＋×2×3×1＝5(立方丈)＝5 000(立方尺)。‎ ‎11．直三棱柱ABC A1B‎1C1中，侧棱长为2，AC＝BC＝1，∠ACB＝90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E.要使AB1⊥平面C1DF，则线段B‎1F的长为(　　)‎ A. B．1 C. D．2‎ ‎【答案】A ‎【解析】选A　设B‎1F＝x，因为AB1⊥平面C1DF，DF⊂平面C1DF，所以AB1⊥DF.由已知可得A1B1＝，设Rt△AA1B1斜边AB1上的高为h，则DE＝h.又2×＝h，所以h＝，DE＝.‎ 在Rt△DB1E中，B1E＝ ＝.由面积相等得× ＝x，得x＝.‎ ‎12． 已知A,B是球O的球面上两点，∠AOB=90,C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为 A．36π B.64π C.144π D.256π ‎【答案】C ‎【解析】如图所示，‎ 当点C位于垂直于面的直径端点时，三棱锥的体积最大，设球的半径为，此时，故，则球的表面积为，故选C．‎ 二、填空题(4*5=20分)‎ ‎13、若直线l的方向向量为a＝(1,0,2)，平面α的法向量为n＝(－2,0，－4)，则直线l与平面α的位置关系为________。‎ ‎【答案】　l⊥α ‎【解析】因为a＝－n，所以l⊥α。‎ ‎14、如图所示，在正方体ABCD－A1B‎1C1D1中，O是底面正方形ABCD的中心，M是D1D的中点，N是A1B1的中点，则直线ON，AM的位置关系是________。‎ ‎【答案】垂直 ‎【解析】以D为坐标原点，DA，DC，DD1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，设DA＝2，则A(2,0,0)，M(0,0,1)，O(1,1,0)，N(2，1,2)，所以＝(－2，0,1)，＝(1,0,2)，·＝－2＋0＋2＝0，所以AM⊥ON。‎ ‎15. 如图所示，在正方体ABCD－A1B‎1C1D1中，M，N分别为棱C1D1，C‎1C的中点。给出下列四个结论：‎ ‎①直线AM与CC1是相交直线；②直线AM与BN是平行直线；‎ ‎③直线BN与MB1是异面直线；④直线MN与AC所成的角为60°。‎ 其中正确结论的序号是________。‎ ‎【答案】③④‎ ‎【解析】(1)只有直线B‎1C1与直线EF在同一平面内，且两者是相交的，直线AA1，A1B1，A1D1与直线EF都是异面直线。故选D。(2)由题图可知AM与CC1是异面直线，AM与BN是异面直线，BN与MB1是异面直线。连接D‎1C，因为D‎1C∥MN，所以∠ACD1即为直线MN与AC所成的角，且∠ACD1＝60°。故③④正确。‎ ‎16．已知正三棱柱ABC－A1B‎1C1的所有顶点都在半径为1的球面上，当正三棱柱的体积最大时，该正三棱柱的高为________。‎ ‎【答案】 ‎【解析】作出正三棱柱ABC－A1B‎1C1如图所示，由题意知，球心O为两底面ABC，A1B‎1C1的中心O1，O2的连线的中点，‎ 设三棱柱的高O1O2＝h，因为球的半径OC＝1，所以在Rt△OO‎2C中，‎ 有O‎2C＝，所以CD＝O‎2C，AB＝CD＝O‎2C，所以VABC－A1B‎1C1＝·AB·CD·O1O2＝×××·h＝(－h3＋4h)，易知当h＝时，三棱柱的体积取得最大值。‎ 二、解答题(6*12=70分)‎ ‎17．如图，在直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．‎ 求证：(1)A1B1∥平面DEC1；(2)BE⊥C1E．‎ ‎【答案】(1)见解析；(2)见解析.‎ ‎【解析】(1)因为D，E分别为BC，AC的中点，所以ED∥AB.在直三棱柱ABC−A1B1C1中，AB∥A1B1，‎ 所以A1B1∥ED.又因为ED⊂平面DEC1，A1B1平面DEC1，所以A1B1∥平面DEC1.‎ ‎(2)因为AB=BC，E为AC的中点，所以BE⊥AC.因为三棱柱ABC−A1B1C1是直棱柱，‎ 所以CC1⊥平面ABC.又因为BE⊂平面ABC，所以CC1⊥BE.因为C1C⊂平面A1ACC1，‎ AC⊂平面A1ACC1，C1C∩AC=C，所以BE⊥平面A1ACC1.因为C1E⊂平面A1ACC1，所以BE⊥C1E.‎ ‎【名师点睛】本小题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识，考查空间想象能力和推理论证能力.‎ ‎18、图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.‎ ‎(1)证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；‎ ‎(2)求图2中的二面角B−CG−A的大小.‎ ‎【答案】(1)见解析；(2).‎ ‎【解析】(1)由已知得ADBE，CGBE，所以ADCG，故AD，CG确定一个平面，‎ 从而A，C，G，D四点共面．由已知得ABBE，ABBC，故AB平面BCGE．‎ 又因为AB平面ABC，所以平面ABC平面BCGE．‎ ‎(2)作EHBC，垂足为H．因为EH平面BCGE，平面BCGE平面ABC，所以EH平面ABC．‎ 由已知，菱形BCGE的边长为2，∠EBC=60°，可求得BH=1，EH=．以H为坐标原点，的方向为x轴的正方向，建立如图所示的空间直角坐标系H–xyz，‎ 则A(–1，1，0)，C(1，0，0)，G(2，0，)，=(1，0，)，=(2，–1，0)．‎ 设平面ACGD的法向量为n=(x，y，z)，则即所以可取n=(3，6，–)．又平面BCGE的法向量可取为m=(0，1，0)，所以．因此二面角B–CG–A的大小为30°．‎ ‎【名师点睛】本题是很新颖的立体几何考题，首先是多面体折叠问题，考查考生在折叠过程中哪些量是不变的，再者折叠后的多面体不是直棱柱，最后通过建系的向量解法将求二面角转化为求二面角的平面角问题，突出考查考生的空间想象能力.‎ ‎19．如图，在四棱锥P–ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且．‎ ‎(1)求证：CD⊥平面PAD；(2)求二面角F–AE–P的余弦值；‎ ‎(3)设点G在PB上，且．判断直线AG是否在平面AEF内，说明理由．‎ ‎【答案】(1)见解析；(2)；(3)见解析.‎ ‎【解析】(1)因为PA⊥平面ABCD，所以PA⊥CD．又因为AD⊥CD，所以CD⊥平面PAD．‎ ‎(2)过A作AD的垂线交BC于点M．因为PA⊥平面ABCD，所以PA⊥AM，PA⊥AD．‎ 如图建立空间直角坐标系A−xyz，则A(0，0，0)，B(2，1，0)，C(2，2，0)，D(0，2，0)，P(0，0，2)．因为E为PD的中点，所以E(0，1，1)．所以．‎ 所以.设平面AEF的法向量为n=(x，y，z)，则即令z=1，则．于是．又因为平面PAD的法向量为p=(1，0，0)，所以.由题知，二面角F−AE−P为锐角，所以其余弦值为．‎ ‎(3)直线AG在平面AEF内．因为点G在PB上，且，‎ 所以.由(2)知，平面AEF的法向量.所以.所以直线AG在平面AEF内.‎ ‎【名师点睛】(1)由题意利用线面垂直的判定定理即可证得题中的结论；‎ ‎(2)建立空间直角坐标系，结合两个半平面的法向量即可求得二面角F−AE−P的余弦值；‎ ‎(3)首先求得点G的坐标，然后结合平面的法向量和直线AG 的方向向量即可判断直线是否在平面内.‎ ‎20．如图，平面，，．‎ ‎(1)求证：平面；(2)求直线与平面所成角的正弦值；‎ ‎(3)若二面角的余弦值为，求线段的长．‎ ‎【答案】(1)见解析；(2)；(3)．‎ ‎【解析】依题意，可以建立以为原点，分别以的方向为轴，轴，轴正方向的空间直角坐标系(如图)，可得，．设，则．‎ ‎(1)依题意，是平面的法向量，又，可得，‎ 又因为直线 平面，所以平面．‎ ‎(2)依题意，．设为平面的法向量，则即不妨令，可得．‎ 因此有．所以，直线与平面所成角的正弦值为．‎ ‎(3)设为平面的法向量，则即 不妨令，可得．由题意，有，解得 ‎．经检验，符合题意．所以，线段的长为．‎ ‎【名师点睛】本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识．考查用空间向量解决立体几何问题的方法．考查空间想象能力、运算求解能力和推理论证能力．‎ ‎21、如图，在三棱锥中，，，为的中点．‎ ‎(1)证明：平面；‎ ‎(2)若点在棱上，且二面角为，‎ 求与平面所成角的正弦值．‎ ‎【答案】(1)见解析；(2)．‎ ‎【解析】(1)因为，为的中点，所以，且，连结．‎ 因为，所以为等腰 直角三角形，且，，由知，由知平面．‎ ‎(2)如图，以为坐标原点，的方向为轴正方向，建立空间直角坐标系．‎ 由已知得，，，，，，‎ 取平面的法向量，设，则，‎ 设平面的法向量为．由，，得，可取，，由已知得，‎ ‎，解得(舍去)，，，又，所以．所以与平面所成角的正弦值为．‎ ‎22、如图，且AD=2BC，,且EG=AD，且CD=2FG，，DA=DC=DG=2.‎ ‎(I)若M为CF的中点，N为EG的中点，求证：；‎ ‎(II)求二面角的正弦值； ‎ ‎(III)若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长. ‎ ‎【答案】(1)证明见解析；(2)；(3)．‎ ‎【解析】依题意，可以建立以为原点，‎ 分别以，，的方向为轴，轴，轴的正方向的空间直角坐标系(如图)，可得，，，，，，，，．‎ ‎(1)依题意，．设为平面的法向量，则即，不妨令，可得．又，可得，‎ 又因为直线平面，所以平面．‎ ‎(2)依题意，可得，，．设为平面的法向量，则即，不妨令，可得．设为平面的法向量，则即，不妨令，可得．因此有，于是．所以，二面角的正弦值为．‎ ‎(3)设线段DP的长为，则点的坐标为，可得．易知，为平面的一个法向量，故，由题意，可得，解得．所以线段的长为．‎ ‎ ‎