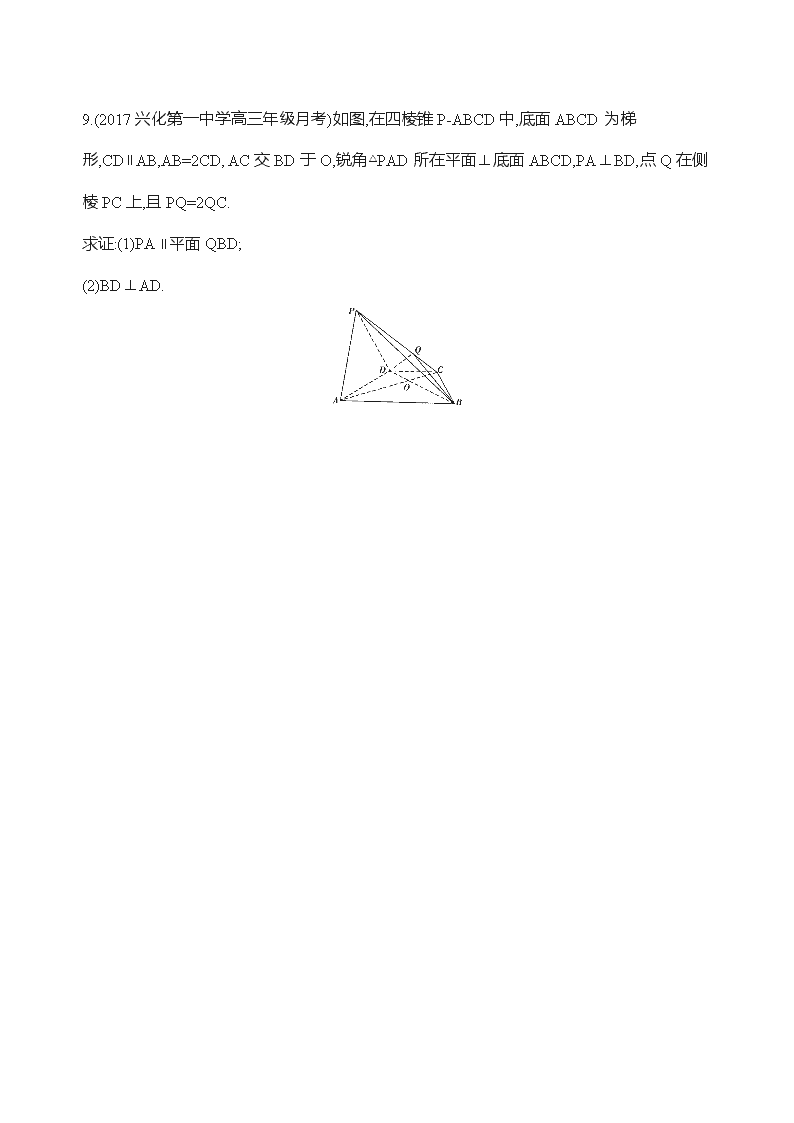2019届二轮复习专题攻略基础滚动小练：第12讲椭圆作业（江苏专用） 4页

‎2019届二轮复习 专题攻略基础滚动小练：第12讲 椭圆 作业（江苏专用）‎ ‎1.已知集合A=,B=.若A∪B=R,则实数t的取值范围是　　　　. ‎ ‎2.(2018扬州高三调研)在平面直角坐标系xOy中,若抛物线y2=2px(p>0)上横坐标为1的点到焦点的距离为4,则该抛物线的焦点到准线的距离为　　　　. ‎ ‎3.(2018常州教育学会学业水平检测)已知实数x,y满足则x+y的取值范围是　　　　. ‎ ‎4.(2018溧水中学月考)函数f(x)=2x+的最小值为　　　　. ‎ ‎5.若椭圆上存在一点与椭圆的两个焦点构成顶角为120°的等腰三角形,则椭圆的离心率为　　　　. ‎ ‎6.(2017镇江高三期末)已知正四棱锥的底面边长为2,侧棱长为,则该正四棱锥的体积为　　　　. ‎ ‎7.已知平面内的四点O,A,B,C满足·=2,·=3,则· =　　　. ‎ ‎8.(2018常州教育学会学业水平检测)如图,在平面直角坐标系xOy中,函数y=sin(ωx+φ)(ω>0,0<φ<π)的图象与x轴的交点A,B,C满足OA+OC=2OB,则φ=　　　　. ‎ ‎9.(2017兴化第一中学高三年级月考)如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.‎ 求证:(1)PA∥平面QBD;‎ ‎(2)BD⊥AD.‎ 答案精解精析 ‎1.答案　(-∞,1)‎ 解析　集合A=(-∞,1)∪[2,+∞),B=(t,+∞),A∪B=R,则t<1. ‎ ‎2.答案　6‎ 解析　抛物线y2=2px(p>0)上横坐标为1的点到焦点的距离为4,则1+=4,p=6.故该抛物线的焦点到准线的距离p=6.‎ ‎3.答案　‎ 解析　不等式组对应的平面区域是以点,(0,2)和(4,4)为顶点的三角形,当x+y经过点时取得最小值,经过点(4,4)时取得最大值8,故x+y的取值范围是.‎ ‎4.答案　5‎ 解析　f(x)=(2x+1)+-1≥2-1=5,当且仅当2x+1=,即x=1时,取等号,则最小值是5.‎ ‎5.答案　或 解析　若以F1F2为底边,则点P为短轴的一个端点,则e1==sin 60°=;若以F1F2为一条腰,则不妨设|PF1|=2c,|PF2|=2c.由椭圆的定义可得|PF1|+|PF2|=2c+2c=2a,此时离心率e2===.‎ ‎6.答案　‎ 解析　正四棱锥的高h==2,则体积V=×22×2=.‎ ‎7.答案　-5‎ 解析　由·=·=·-·=2,·=·(-)=·-·=3,两式相加,可得·-·=·=5.故·=-·=-5.‎ ‎8.答案　‎ 解析　设A(x,0),最小正周期T=,则C,B.由OA+OC=2OB,得x+x+=2.解得x=.所以y=f=sin ‎=sin=1.又0<φ<π,所以φ=.‎ ‎9.证明　(1)如图,连接OQ.因为AB∥CD,AB=2CD,所以AO=2OC.又PQ=2QC,所以PA∥OQ.‎ 又OQ⊂面QBD,PA⊄面QBD,所以PA∥平面QBD.‎ ‎(2)在平面PAD内过P作PH⊥AD于H,如图.‎ 因为侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,‎ PH⊂平面PAD,所以PH⊥平面ABCD.‎ 又BD⊂平面ABCD,所以PH⊥BD.又PA⊥BD,且PA∩PH=P,PH⊂平面PAD,PA⊂平面PAD,‎ 所以BD⊥平面PAD.‎ 又AD⊂平面PAD,所以BD⊥AD.‎ ‎　　‎