2019届二轮复习高考解答题突破(四)　空间向量与立体几何学案（全国通用） 27页

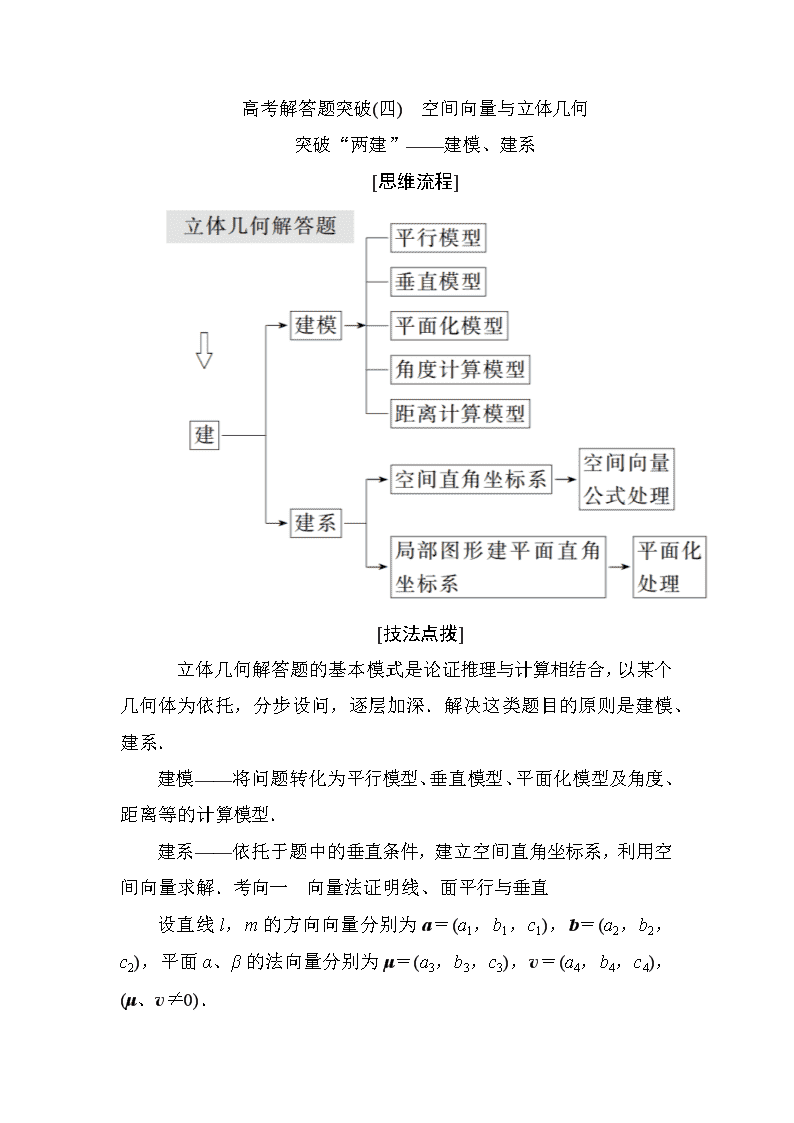
高考解答题突破(四)　空间向量与立体几何 突破“两建”——建模、建系 ‎[思维流程]‎ ‎ [技法点拨]‎ ‎　立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深．解决这类题目的原则是建模、建系．‎ 建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型．‎ 建系——依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解．考向一　向量法证明线、面平行与垂直 设直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2，c2)，平面α、β的法向量分别为μ＝(a3，b3，c3)，v＝(a4，b4，c4)，(μ、v≠0)．‎ ‎(1)线面平行：l∥α⇔a⊥μ⇔a·μ＝0⇔a1a3＋b1b3＋c1c3＝0.‎ ‎(2)线面垂直：l⊥α⇔a∥μ⇔a＝kμ⇔a1＝ka3，b1＝kb3，c1＝kc3.‎ ‎(3)面面平行：α∥β⇔μ∥v⇔μ＝λv⇔a3＝λa4，b3＝λb4，c3＝λc4.‎ ‎(4)面面垂直：α⊥β⇔μ⊥v⇔μ·v＝0⇔a3a4＋b3b4＋c3c4＝0.‎ ‎ [探究追问]　本例用几何方法如何证明？谈谈你对两种方法的认识．‎ ‎[证明]　(1)在直三棱柱中有BB1⊥AB.又AB⊥BC，BB1∩BC＝B，‎ ‎∴AB⊥平面BCC1B1，∵B1D⊂平面BCC1B1，‎ ‎∴AB⊥B1D.‎ 在矩形BCC1B1中，D为CC1的中点，且DC＝BC＝DC1＝2，∴∠BDC＝∠B1DC1＝45°，‎ ‎∴∠BDB1＝90°，即B1D⊥BD.‎ 又∵AB∩BD＝B.‎ ‎∴B1D⊥平面ABD.‎ ‎(2)取BB1的中点H，则HC1∥BD.‎ ‎∵B1E＝1，B1H＝2，∴E为B1H的中点．‎ ‎∵F为B1C1的中点，∴EF∥HC1，∴EF∥BD.‎ ‎∵EF⊄平面ABD，BD⊂平面ABD，∴EF∥平面ABD.‎ 又G为A1C1的中点，∴GF∥A1B1∥AB，‎ ‎∵GF⊄平面ABD，AB⊂平面ABD，∴GF∥平面ABD.‎ 又∵GF∩EF＝F，∴平面EGF∥平面ABD.‎ ‎　向量法证明平行与垂直的4个步骤 ‎(1)建立空间直角坐标系，建系时，要尽可能地利用载体中的垂直关系．‎ ‎(2)建立空间图形与空间向量之间的关系，用空间向量表示出问题中所涉及的点、直线、平面的要素．‎ ‎(3)通过空间向量的运算求出平面向量或法向量，再研究平行、垂直关系．‎ ‎(4)根据运算结果解释相关问题．‎ ‎[对点训练]‎ ‎1．(2018·福州质检)如图，在四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD是菱形，PA＝AB＝2，∠BAD＝60°，E是PA的中点．‎ ‎(1)求证：直线PC∥平面BDE；‎ ‎(2)求证：BD⊥PC.‎ ‎[证明]　设AC∩BD＝O.因为∠BAD＝60°，AB＝2，底面ABCD为菱形，所以BO＝1，AO＝CO＝，AC⊥BD.‎ 如图，以O为坐标原点，以OB，OC所在直线分别为x轴，y轴，过点O且平行于PA的直线为z轴，建立空间直角坐标系O－xyz，‎ 则P(0，－，2)，A(0，－，0)，B(1,0,0)，C(0，，0)，D(－1,0,0)，E(0，－，1)．‎ ‎(1)设平面BDE的法向量为n1＝(x1，y1，z1)，因为＝(－1，－，1)，＝(－2,0,0)，‎ 由得 令z1＝，得y1＝1，所以n1＝(0,1，)．‎ 又＝(0,2，－2)，所以·n1＝0＋2－2＝0，‎ 即⊥n1，又PC⊄平面BDE，‎ 所以PC∥平面BDE.‎ ‎(2)因为＝(0,2，－2)，＝(－2,0,0)，‎ 所以·＝0.‎ 故BD⊥PC.‎ 考向二　向量法求直线与平面所成的角 求出平面的法向量n，直线的方向向量a，设线面所成的角为θ，则sinθ＝|cosn，a|＝.‎ ‎[解]　(1)证明：因为四边形ABCD为矩形，‎ 所以△AEF∽△CBF，所以＝＝＝.‎ 又矩形ABCD中，AB＝1，AD＝，‎ 所以AE＝，AC＝.‎ 在Rt△BEA中，BE＝＝，‎ 所以AF＝AC＝，BF＝BE＝.‎ 在△ABF中，AF2＋BF2＝2＋2＝1＝AB2，‎ 所以∠AFB＝90°，‎ ‎　求直线与平面所成角应注意的两点 ‎(1)准确求出平面的法向量．‎ ‎(2)直线和平面所成的角的正弦值等于直线的方向向量与平面法向量夹角的余弦值的绝对值，即注意函数名称的变化．‎ ‎[对点训练]‎ ‎2．(2018·昆明质检)如图，在直三棱柱ABC—A1B1C1中，M是AB的中点．‎ ‎(1)求证：BC1∥平面MCA1.‎ ‎(2)若△BMC是正三角形，且AB＝BC1，求直线AB与平面MCA1所成角的正弦值．‎ ‎[解]　(1)证明：连接AC1，设AC1与 A1C的交点为N，则N为AC1的中点，连接MN.‎ 又因为M是AB的中点，所以MN∥BC1.‎ 因为MN⊂平面MCA1，BC1⊄平面MCA1，‎ 所以BC1∥平面MCA1.‎ ‎(2)因为M是AB的中点，△BMC是正三角形，‎ 所以∠ABC＝60°，∠BAC＝30°，∠ACB＝90°.‎ 因为AB＝BC1，所以AC＝CC1.‎ 设BC＝1，则AC＝CC1＝.‎ 以C为原点，CC1为x轴，CB为y轴，CA为z轴建立如图的空间直角坐标系，则C(0,0,0)，B(0,1,0)，A(0,0，)，A1(，0，)，M，‎ 所以＝(0,1，－)，＝，＝(，0，)．‎ 设n＝(x，y，z)是平面MCA1的一个法向量，则 即令x＝1，得y＝，z＝－1.‎ 所以平面MCA1的一个法向量为n＝(1，，－1)．‎ 则|cos〈，n〉|＝＝.‎ 所以直线AB与平面MCA1所成角的正弦值为.‎ ‎　　　　　　　　　　　　　　　　　‎ ‎ [解]　(1)证明：因为AP＝CP＝AC＝4，O为AC的中点，所以OP⊥AC，且OP＝2.‎ 连接OB.因为AB＝BC＝AC，所以△ABC为等腰直角三角形，且OB⊥AC，OB＝AC＝2.‎ ‎　利用向量求二面角问题的策略 ‎(1)求空间中二面角的大小，可根据题意建立空间直角坐标系，再分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．‎ ‎(2)给出二面角的大小求解或证明相关问题，可利用求解二面角的方法列出相关的关系式，再根据具体问题求解．‎ ‎[对点训练]‎ ‎3．如图1，正方形ABCD的边长为4，AB＝AE＝BF＝EF，AB∥‎ EF.把四边形ABCD沿AB折起，使得AD⊥平面AEFB，点G是EF的中点，连接AG，CG，BE，CE，CA，如图2.‎ ‎(1)求证：AG⊥平面BCE.‎ ‎(2)求二面角C－AE－F的余弦值．‎ ‎[解]　(1)证明：连接BG.‎ 因为BC∥AD，AD⊥底面AEFB，所以BC⊥底面AEFB.‎ 又因为AG⊂底面AEFB，‎ 所以BC⊥AG.‎ 又因为AB∥EG，AB＝EF＝EG，AB＝AE，‎ 所以四边形ABGE为菱形，所以AG⊥BE.‎ 又因为BC∩BE＝B，BE⊂平面BCE，BC⊂平面BCE，‎ 所以AG⊥平面BCE.‎ ‎(2)由(1)知四边形ABGE为菱形，AG⊥BE，AE＝EG＝BG＝AB＝4.‎ 设AG∩BE＝O，则由题计算可得OE＝OB＝2，OA＝OG＝2.‎ 以点O为坐标原点，建立如图所示的空间直角坐标系O－xyz，‎ 则O(0,0,0)，A(－2,0,0)，E(0，－2，0)，F(4,2，0)，C(0,2，4)，D(－2,0,4)，‎ 所以＝(2,2，4)，＝(2，－2，0)．‎ 设平面ACE的一个法向量为n＝(x，y，z)，‎ 则所以 令y＝1，则 可取n＝(，1，－)．‎ 又易知平面AEF的一个法向量为＝(0,0,4)，‎ 设二面角C－AE－F的大小为θ，由图易知θ∈，‎ 所以cosθ＝＝＝.‎ 考向四　立体几何中的探索性问题 ‎1．条件追溯型 解决此类问题的基本策略是执果索因．其结论明确，需要求出使结论成立的充分条件，可将题设和结论都视为已知条件，即可迅速找出切入点．‎ ‎2．存在判断型 解决此类问题的策略：通常假设题中的数学对象存在(或结论成立)，然后在这个前提下进行逻辑推理，若能推导出与条件吻合的数据或事实，则说明假设成立，即存在；若推导出与条件或实际情况相矛盾的结论，则说明假设不成立，即不存在．‎ ‎ [解]　(1)证明：连接BD，由于四边形ABCD是菱形，∠DAB＝，E是AB的中点，‎ 所以DE⊥AB，‎ 因为四边形ADNM是矩形，平面ADNM⊥平面ABCD且交线为AD，‎ 所以MA⊥平面ABCD，‎ ‎　向量法解决探索性问题的4步 第一步　建立坐标系：根据条件建立空间直角坐标系，必要时需证明线线垂直，求出相应点的坐标．‎ 第二步　求向量坐标：求直线的方向向量或平面的法向量的坐标，存在性问题一般用参数表示．‎ 第三步　求参数值：利用公式得出空间角的三角函数值或参数值．‎ 第四步　下结论：根据角的范围核查结果，存在性问题依据参数值作出判断．‎ ‎[对点训练]‎ ‎4.如图所示，四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD＝NB＝1，E为BC的中点．‎ ‎(1)求异面直线NE与AM所成角的余弦值；‎ ‎(2)在线段AN上是否存在点S，使得ES⊥平面AMN？若存在，求线段AS的长；若不存在，请说明理由．‎ ‎[解]　(1)如图所示，以D为坐标原点，建立空间直角坐标系D－xyz.‎ 依题意得D(0,0,0)，A(1,0,0)，M(0,0,1)，C(0,1,0)，B(1,1,0)，N(1,1,1)，E，所以＝，＝(－1，0,1)，因为 ‎|cos〈，〉|＝＝＝.‎ 所以异面直线NE与AM所成角的余弦值为.‎ ‎(2)假设在线段AN上存在点S，使得ES⊥平面AMN.连接AE，如图所示．‎ 因为＝(0,1,1)，可设＝λ＝(0，λ，λ)，‎ 又＝，‎ 所以＝＋＝.由ES⊥平面AMN，‎ 得即解得λ＝，此时＝‎ ，||＝.‎ 经检验，当|AS|＝时，ES⊥平面AMN.‎ 故线段AN上存在点S，使得ES⊥平面AMN，此时|AS|＝.‎ 专题跟踪训练(二十三)‎ ‎1．如图，过底面是矩形的四棱锥F－ABCD的顶点F作EF∥AB，使AB＝2EF，且平面ABFE⊥平面ABCD，若点G在CD上且满足DG＝GC.求证：‎ ‎(1)FG∥平面AED.‎ ‎(2)平面DAF⊥平面BAF.‎ ‎[证明]　(1)因为DG＝GC，AB＝CD＝2EF，AB∥EF∥CD，‎ 所以EF∥DG，EF＝DG.‎ 所以四边形DEFG为平行四边形，‎ 所以FG∥ED.‎ 又因为FG⊄平面AED，ED⊂平面AED，‎ 所以FG∥平面AED.‎ ‎(2)因为平面ABFE⊥平面ABCD，平面ABFE∩平面ABCD＝AB，AD⊥AB，且AD⊂平面ABCD，‎ 所以AD⊥平面BAF.‎ 又因为AD⊂平面DAF.‎ 所以平面DAF⊥平面BAF.‎ ‎2．(2018·安徽合肥一模)如图所示，在四棱台ABCD－A1B1C1D1中，AA1⊥底面ABCD，四边形ABCD为菱形，∠BAD＝120°，AB＝AA1＝2A1B1＝2.‎ ‎(1)若M为CD的中点，求证：AM⊥平面AA1B1B.‎ ‎(2)求直线DD1与平面A1BD所成角的正弦值．‎ ‎[解]　(1)证明：连接AC.∵四边形ABCD为菱形，∠BAD＝120°，‎ ‎∴△ACD为等边三角形．又∵点M为CD的中点，∴AM⊥CD.‎ 由CD∥AB得，AM⊥AB.∵AA1⊥底面ABCD，AM⊂底面ABCD，∴AM⊥AA1.‎ 又∵AB∩AA1＝A，AB⊂平面AA1B1B，AA1⊂平面AA1B1B，∴AM⊥平面AA1B1B.‎ ‎(2)∵四边形ABCD为菱形，∠BAD＝120°，AB＝AA1＝2A1B1＝2，∴DM＝1，AM＝，∠AMD＝∠BAM＝90°.‎ 又∵AA1⊥底面ABCD，则可分别以AB，AM，AA1所在的直线为 x轴、y轴、z轴，建立如图所示的空间直角坐标系A－xyz，‎ 则A1(0,0,2)，B(2,0,0)，D(－1，，0)，D1，‎ ‎∴＝，＝(－3，，0)，＝(2,0，－2)．‎ 设平面A1BD的一个法向量n＝(x，y，z)，‎ 则有得即y＝x＝z.‎ 令x＝1，则n＝(1，，1)．‎ ‎∴直线DD1与平面A1BD所成角θ的正弦值为 sinθ＝|cos〈n，〉|＝＝.‎ ‎3．(2018·全国卷Ⅲ)如图，边长为2的正方形ABCD所在的平面与半圆弧所在平面垂直，M是上异于C，D的点．‎ ‎(1)证明：平面AMD⊥平面BMC；‎ ‎(2)当三棱锥M－ABC体积最大时，求面MAB与面MCD所成二面角的正弦值．‎ ‎[解]　(1)证明：由题设知，平面CMD⊥平面ABCD，交线为CD.因为BC⊥CD，BC⊂平面ABCD，所以BC⊥平面CMD，故BC⊥DM.‎ 因为M为上异于C，D的点，且DC为直径，所以DM⊥CM.‎ 又BC∩CM＝C，所以DM⊥平面BMC.‎ 而DM⊂平面AMD，故平面AMD⊥平面BMC.‎ ‎(2)以D为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系D－xyz.‎ 当三棱锥M－ABC体积最大时，M为的中点．‎ 由题设得D(0,0,0)，A(2,0,0)，B(2,2,0)，C(0,2,0)，M(0,1,1)，＝(－2,1,1)，＝(0,2,0)，＝(2,0,0)．‎ 设n＝(x，y，z)是平面MAB的法向量，则 即 可取n＝(1,0,2)．‎ 是平面MCD的法向量，因此 cos〈n，〉＝＝，sin〈n，〉＝.‎ ‎4．(2018·沈阳二模)如图，在四边形ABCD中，AB∥CD，∠BCD ‎＝，四边形ACFE为矩形，且CF⊥平面ABCD，AD＝CD＝BC＝CF.‎ ‎(1)求证：EF⊥平面BCF；‎ ‎(2)点M在线段EF上运动，当点M在什么位置时，平面MAB与平面FCB所成锐二面角最大，并求此时二面角的余弦值．‎ ‎[解]　(1)证明：在梯形ABCD中，设AD＝CD＝BC＝1，‎ ‎∵AB∥CD，∠BCD＝，∴AB＝2，∴AC2＝AB2＋BC2－‎ ‎2AB·BC·cos＝3.‎ ‎∴AB2＝AC2＋BC2，∴BC⊥AC.‎ ‎∵CF⊥平面ABCD，AC⊂平面ABCD，‎ ‎∴AC⊥CF，而CF∩BC＝C，‎ ‎∴AC⊥平面BCF.‎ ‎∵四边形ACFE是矩形，∴EF∥AC，∴EF⊥平面BCF.‎ ‎(2)由(1)，以CA，CB，CF所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，‎ 设AD＝CD＝BC＝CF＝1，令FM＝λ(0≤λ≤)，则C(0,0,0)，A(，0,0)，B(0,1,0)，M(λ，0,1)，‎ ‎∴＝(－，1,0)，＝(λ，－1,1)，‎ 设平面MAB的法向量为n1＝(x，y，z)，‎ 则即 令x＝1，则n1＝(1，，－λ)，为平面MAB的一个法向量．‎ 易知n2＝(1,0,0)是平面FCB的一个法向量，‎ 设平面MAB与平面FCB所成锐二面角为θ，‎ 则cosθ＝＝ ‎＝.‎ ‎∵0≤λ≤，∴当λ＝0时，cosθ有最小值，‎ ‎∴点M与点F重合时，平面MAB与平面FCB所成锐二面角最大，此时二面角的余弦值为.‎