高一数学（人教A版）必修4能力提升：本册综合能力测试 14页

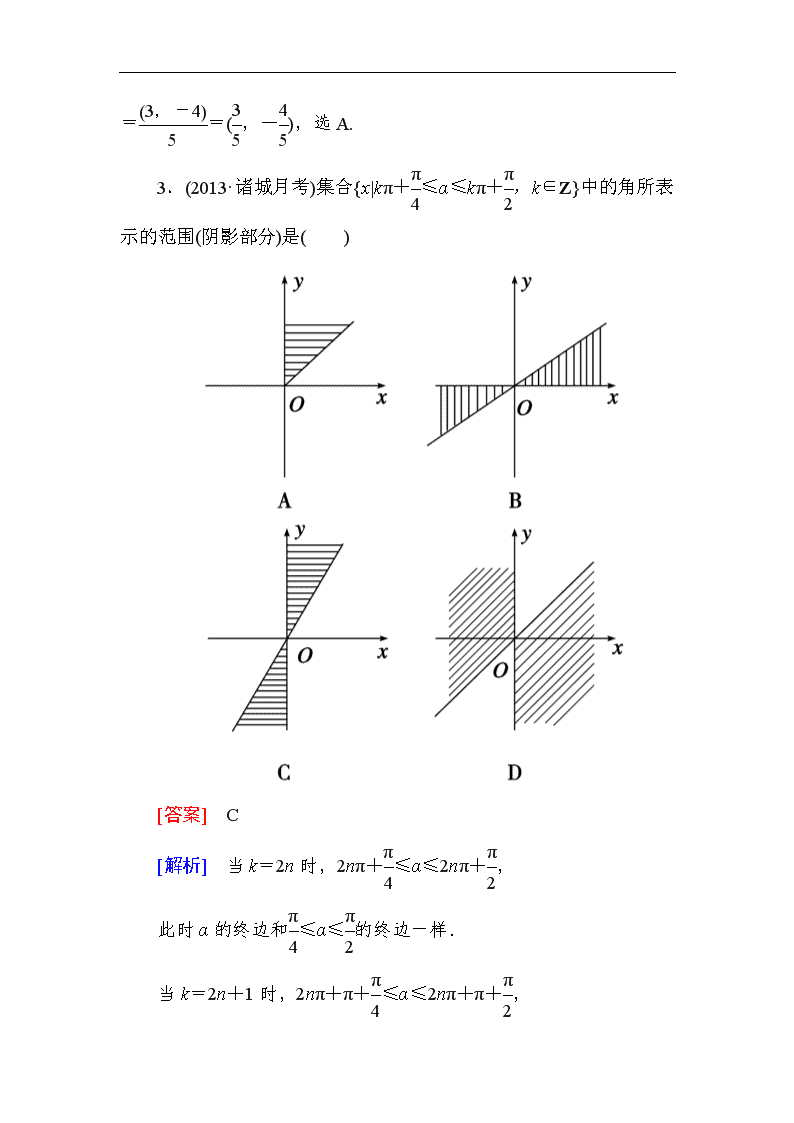
本册综合能力测试 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。‎ 第Ⅰ卷(选择题　共60分)‎ 一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)‎ ‎1．(2013·泰安期末)tanπ的值为(　　)‎ A.　　　B．－　　　C.　　　D．－ ‎[答案]　D ‎[解析]　tanπ＝tan(2π＋π)＝tanπ＝－.‎ ‎2．(2013·辽宁理)已知点A(1,3)，B(4，－1)，则与向量同方向的单位向量为(　　)‎ A．(，－) B．(，－)‎ C．(－，) D．(－，)‎ ‎[答案]　A ‎[解析]　本题考查平面向量的坐标运算，单位向量的求法．‎ 因为＝(3，－4)，||＝5，所以与向量同向的单位向量为＝ ‎＝(，－)，选A.‎ ‎3．(2013·诸城月考)集合{x|kπ＋≤α≤kπ＋，k∈Z}中的角所表示的范围(阴影部分)是(　　)‎ ‎[答案]　C ‎[解析]　当k＝2n时，2nπ＋≤α≤2nπ＋，‎ 此时α的终边和≤α≤的终边一样．‎ 当k＝2n＋1时，2nπ＋π＋≤α≤2nπ＋π＋，‎ 此时α的终边和π＋≤α≤π＋的终边一样．‎ ‎4．已知扇形的周长为‎8 cm，圆心角为2弧度，则该扇形的面积为(　　)‎ A．‎4 cm2 B．‎6 cm2 ‎ C．‎8 cm2 D．‎16 cm2‎ ‎[答案]　A ‎[解析]　由题意得解得 所以S＝lr＝4(cm2)．‎ ‎5．已知α是锐角，a＝(，sinα)，b＝(cosα，)，且a∥b，则α为(　　)‎ A．15° B．45° ‎ C．75° D．15°或75°‎ ‎[答案]　D ‎[解析]　∵a∥b，∴sinα·cosα＝×，‎ 即sin2α＝ 又∵α为锐角，∴0°<2α<180°.‎ ‎∴2α＝30°或2α＝150°‎ 即α＝15°或α＝75°.‎ ‎6．若sinα＝，α∈，则tan2α的值为(　　)‎ A. B. ‎ C．－ D．－ ‎[答案]　B ‎[解析]　∵sinα＝，α∈，‎ ‎∴cosα＝－.∴tanα＝－.‎ ‎∴tan2α＝＝.‎ ‎7．(2013烟台模拟)已知cosα＝，cos(α＋β)＝－，α，β都是锐角，则cosβ＝(　　)‎ A．－ B．－ ‎ C. D. ‎[答案]　C ‎[解析]　∵α、 β是锐角，‎ ‎∴0<α＋β<π，又cos(α＋β)＝－<0‎ ‎∴<α＋β<π，∴sin(α＋β)＝ sinα＝，又cosβ＝cos(α＋β－β)‎ ‎＝cos(α＋β)cosα＋sin(α＋β)sinα ‎＝－×＋× ‎＝.‎ ‎8．函数y＝sinx(≤x≤)的值域是(　　)‎ A．[－1,1] B．[，1]‎ C．[，] D．[，1]‎ ‎[答案]　B ‎[解析]　可以借助单位圆或函数的图象求解．‎ ‎9．要得到函数y＝3sin(2x＋)的图象，只需将函数y＝3sin2x的图象(　　)‎ A．向左平移个单位 B．向右平移个单位 C．向左平移个单位 D．向右平移个单位 ‎[答案]　C ‎10．已知a＝(1，－1)，b＝(x＋1，x)，且a与b的夹角为45°，则x的值为(　　)‎ A．0 B．－1‎ C．0或－1 D．－1或1‎ ‎[答案]　C ‎[解析]　由夹角公式：cos45°＝＝，即x2＋x＝0，解得x＝0或x＝－1.‎ ‎11．(2012·全国高考江西卷)若＝，则tan2α＝(　　)‎ A．－ B. ‎ C．－ D. ‎[答案]　B ‎[解析]　主要考查三角函数的运算，分子分母同时除以cosα可得tanα＝－3，带入所求式可得结果．‎ ‎12．设a＝sin17°cos45°＋cos17°sin45°，b＝2cos213°－1，c＝，则有(　　)‎ A．ca>c.‎ 第Ⅱ卷(非选择题　共90分)‎ 二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)‎ ‎13．若tanα＝3，则sinαcosα的值等于________．‎ ‎[答案]　 ‎[解析]　sinαcosα＝＝＝＝.‎ ‎14．已知：|a|＝2，|b|＝，a与b的夹角为，要λb－a与a垂直，则λ为________．‎ ‎[答案]　2‎ ‎[解析]　由题意a·(λb－a)＝0，即λa·b－|a|2＝0，∴λ·2××－4＝0，即λ＝2.‎ ‎15．(2013南通调研)设α、 β∈(0，π)，且sin(α＋β)＝，tan＝，则cosβ的值为________．‎ ‎[答案]　－ ‎[解析]　由tan＝得 sinα＝＝＝ cosα＝ 由sin(α＋β)＝＝＝＝.‎ ‎19．(本题满分12分)(2011～2012浙江调研)设向量α＝(sin 2x，sin x＋cos x)，β＝(1，sinx－cosx)，其中x∈R，函数f(x)＝α·β.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)若f(θ)＝，其中0<θ<，求cos(θ＋)的值．‎ ‎[解析]　(1)由题意得f(x)＝sin2x＋(sinx＋cosx)·(sinx－cosx)＝sin2x－cos2x＝2sin(2x－)，‎ 故f(x)的最小正周期T＝＝π.‎ ‎(2)由(1)知，f(θ)＝2sin(2θ－)，若f(θ)＝，‎ 则sin(2θ－)＝.‎ 又因为0<θ<，所以－<2θ－<，则2θ－＝或2θ－＝，故θ＝或θ＝.‎ 当θ＝时，cos(θ＋)＝cos(＋)＝coscos－sinsin＝.‎ 当θ＝时，cos(θ＋)＝cos(＋)＝cos(π－)＝－cos＝－cos(＋)＝－.‎ ‎20．(本题满分12分)(2012济宁模拟)已知向量a＝(cosθ，sinθ)，θ∈[0，π]，向量b＝(，－1)．‎ ‎(1)若a⊥b，求θ的值；‎ ‎(2)若|‎2a－b|4.‎ ‎21．(本题满分12分)(2013山东潍坊高一期末)已知函数f(x)＝Asin(ωx＋φ)(ω>0,0<φ<)的部分图象如图所示．‎ ‎(Ⅰ)求f(x)的解析式；‎ ‎(Ⅱ)将函数y＝f(x)的图象上所有点的纵坐标不变，横坐标缩短为原来的倍，再将所得函数图象向右平移个单位，得到函数y＝g(x)的图象，求g(x)的单调递增区间；‎ ‎(Ⅲ)当x∈[－，]时，求函数y＝f(x＋)－f(x＋)的最值．‎ ‎[解析]　(Ⅰ)由图得：T＝π－＝π＝π，‎ ‎∴T＝2π，‎ ‎∴ω＝＝1.‎ 又f(π)＝0，得：Asin(π＋φ)＝0，‎ ‎∴π＋φ＝2kπ，φ＝2kπ－π，‎ ‎∵0<φ<，∴当k＝1时，φ＝.‎ 又由f(0)＝2，得：Asinφ＝2，A＝4，‎ ‎∴f(x)＝4sin(x＋)．‎ ‎(Ⅱ)将f(x)＝4sin(x＋)的图象上所有点的横坐标缩短为原来的倍，纵坐标不变得到y＝4sin(2x＋)，再将图象向右平移个单位得到g(x)＝4sin[2(x－)＋]＝4sin(2x－)，‎ 由2kπ－≤2x－≤2kπ＋(k∈Z)得：‎ kπ－≤x≤kπ＋(k∈Z)，‎ ‎∴g(x)的单调增区间为[kπ－，kπ＋](k∈Z)．‎ ‎(Ⅲ)y＝f(x＋)－f(x＋)‎ ‎＝4sin[(x＋)＋]－×4sin[(x＋)＋]‎ ‎＝4sin(x＋)－4sin(x＋)‎ ‎＝4(sinx·cos＋cosx·sin)－4cosx ‎＝2sinx＋2cosx－4cosx＝2sinx－2cosx ‎＝4sin(x－)．‎ ‎∵x∈[－，π]，x－∈[－π，]，‎ ‎∴sin(x－)∈[－1，]，‎ ‎∴函数的最小值为－4，最大值为2.‎ ‎22．(本题满分12分)(2012·全国高考山东卷)已知向量m＝(sinx,1)，n＝(Acosx，cos2x)(A>0)，函数f(x)＝m·n的最大值为6.‎ ‎(Ⅰ)求A；‎ ‎(Ⅱ)将函数y＝f(x)的图象像左平移个单位，再将所得图象各点的横坐标缩短为原来的倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)在上的值域。‎ ‎[解析]　(Ⅰ)f(x)＝m·n＝Acosxsinx＋cos2x＝Asin2x＋cos2x＝Asin，则A＝6；‎ ‎(Ⅱ)函数y＝f(x)的图象向左平移个单位得到函数y＝6sin的图象，再将所得图象各点的横坐标缩短为原来的倍，纵坐标不变，得到函数g(x)＝6sin(4x＋)．‎ 当x∈时，4x＋∈，sin(4x＋)∈，g(x)∈[－3,6]‎ 故函数g(x)在上的值域为[－3,6]．‎