数学文卷·2018届广东省北京师范大学东莞石竹附属学校高二下学期期中考试（2017-04） 10页

www.ks5u.com【来源：全,品…中&高*考+网】‎ ‎2016—17学年第二学期期中测试 高二文科数学 命题人：黄光熙 本试卷共22题，满分150，考试用时120分钟。‎ 一、选择题 ‎1.在△ABC中，若a=2，b=2，A=30°，则B为( )‎ A.60° B.60°或120° C.30° D.30°或150°‎ ‎2.椭圆的离心率为( )‎ A. B. C. D.‎ ‎3.复数的虚部是( )‎ A.i B.-i C.1 D.-1‎ ‎4.ac2＞bc2是a＞b的( )‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎5.在极坐标系中，点（2，）到直线ρ（cosθ+sinθ）=6的距离为( )‎ A.4 B.3 C.2 D.1‎ ‎6.从某大学随机抽取的5名女大学生的身高x（厘米）和体重y（公斤）数据如表 x ‎165‎ ‎160‎ ‎175‎ ‎155‎ ‎170‎ y ‎58‎ ‎52‎ ‎62‎ ‎43‎ ‎60‎ 根据上表可得回归直线方程为则=( )‎ A.-96.8 B.96.8 C.-104.4 D.104.4‎ ‎7.若数列{an}中，an=43-3n，则Sn最大值n=( )‎ A.13 B.14 C.15 D.14或15‎ ‎8.如果命题p∨q是真命题，命题￢p是假命题，那么( )‎ A.命题p一定是假命题 B.命题q一定是假命题 C.命题q一定是真命题 D.命题q是真命题或假命题 ‎9.复数，(m，A，B∈R)，且A+B=0，则m的值是( )‎ A. B. C. 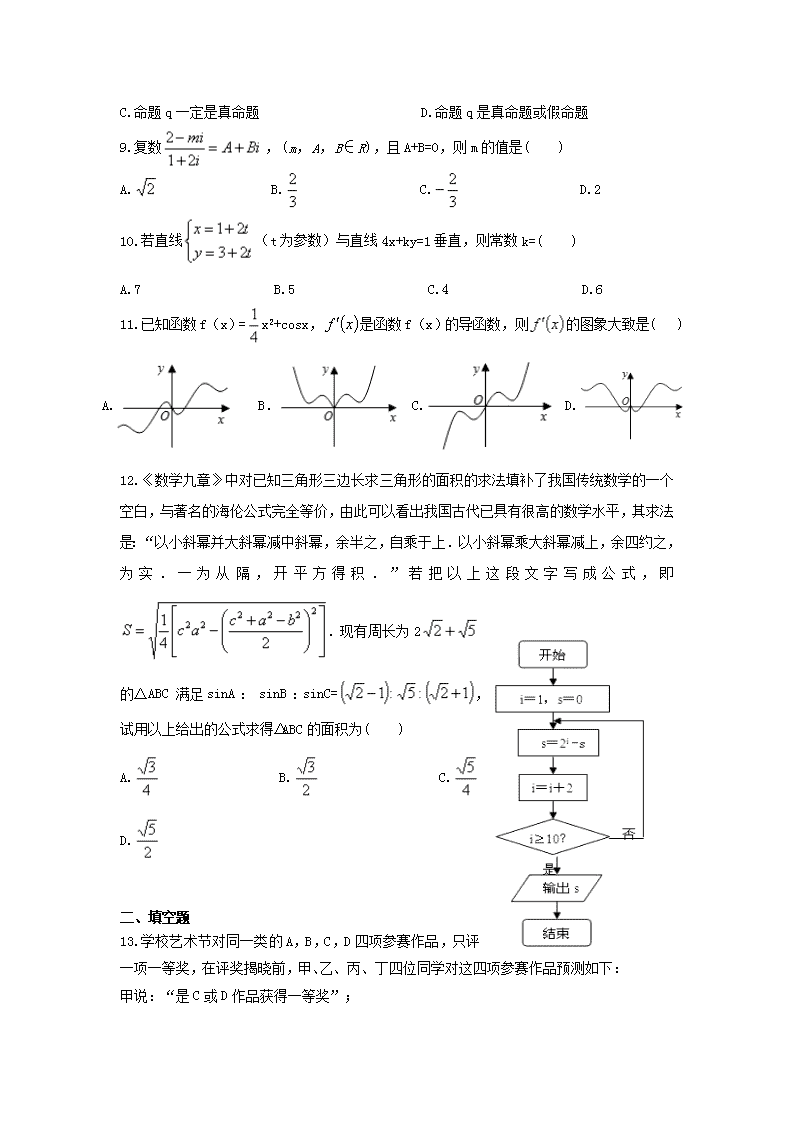D.2‎ ‎10.若直线（t为参数）与直线4x+ky=1垂直，则常数k=( )‎ A.7 B.5 C.4 D.6‎ ‎11.已知函数f（x）=x2+cosx，是函数f（x）的导函数，则的图象大致是( )‎ A.‎ B．‎ C.‎ D.‎ ‎12.《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂减上，余四约之，为实．一为从隔，开平方得积．”若把以上这段文字写成公式，即.现有周长为2的△ABC满足sinA： sinB：sinC=，试用以上给出的公式求得△ABC的面积为( )‎ A. B. C. D.‎ 二、填空题 ‎13.学校艺术节对同一类的A，B，C，D四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下： 甲说：“是C或D作品获得一等奖”‎ ‎； 乙说：“B作品获得一等奖”； 丙说：“A，D两项作品未获得一等奖”； 丁说：“是C作品获得一等奖”． 若这四位同学中只有两位说的话是对的，则获得一等奖的作品是 .‎ ‎14.曲线f（x）=x3+x在（1，f（1））处的切线方程为 .‎ ‎15.某程序框图如图所示，该程序运行后输出的s值为 .‎ ‎16.已知O是坐标原点，点A（-1，1）．若点M（x，y）为平面区域上的一个动点，则的取值范围是 .‎ 三、解答题 ‎17.已知命题p：“对任意x∈，x2-a≥0”，命题q：“存在x∈R，x2+2ax+2-a=0”.若命题“p且q”是真命题，求实数a的取值范围．‎ ‎18.随着“全面二孩”政策推行，我市将迎来生育高峰．今年新春伊始，莞城各医院产科就已经是一片忙碌，至今热度不减．卫生部门进行调查统计，期间发现各医院的新生儿中，不少都是“二孩”；在市第一医院，共有40个猴宝宝降生，其中20个是“二孩”宝宝；市妇幼保健院共有30个猴宝宝降生，其中10个是“二孩”宝宝． （I）从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询． ①在市第一医院出生的一孩宝宝中抽取多少个？ ②若从7个宝宝中抽取两个宝宝进行体检，求这两个宝宝恰出生不同医院且均属“二孩”的概率； （Ⅱ）根据以上数据，能否有85%的把握认为一孩或二孩宝宝的出生与医院有关？ 附：‎ P（k2＞k0）‎ ‎0.4‎ ‎0.25‎ ‎0.15‎ ‎0.10 ‎ k0‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎ 2.706‎ ‎19.已知f（x）=2，集合M={x||f（x）|=2，x＞0}，把M中的元素从小到大依次排成一列，得到数列{an}，n∈N*． （1）求数列{an}的通项公式； （2）记bn=，设数列{bn}的前n项和为Tn，求证Tn＜．‎ ‎20.已知椭圆C的对称中心为原点O，焦点在x轴上，左右焦点分别为F1和F2，且|F1F2|=2，点（1，）在该椭圆上. （1）求椭圆C的方程； （2）过F1的直线l与椭圆C相交于A，B两点，若△AF2B的面积为，求以F2为圆心且与直线l相切圆的方程．‎ ‎21.已知函数f（x）=（k为常数，e=2.71828…是自然对数的底数），曲线y=f（x）在点（1，f（1））处的切线与x轴平行． （1）求k的值； （2）求f（x）的单调区间．‎ ‎22.若以直角坐标系xOy的O为极点，Ox为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程是ρ=． （1）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线； （2）若直线l的参数方程为（t为参数）当直线l与曲线C相交于A，B两点，求||．‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 选项 B A C A D A B D C C A A ‎13. B .‎ ‎14. .‎ ‎15. 482 .‎ ‎16. .‎ ‎17.‎ ‎18.‎ ‎19.‎ ‎20.‎ ‎21.‎ ‎22.‎ ‎ ‎