2021届课标版高考文科数学大一轮复习精练：§8-1 空间几何体的三视图、表面积和体积（试题部分） 23页

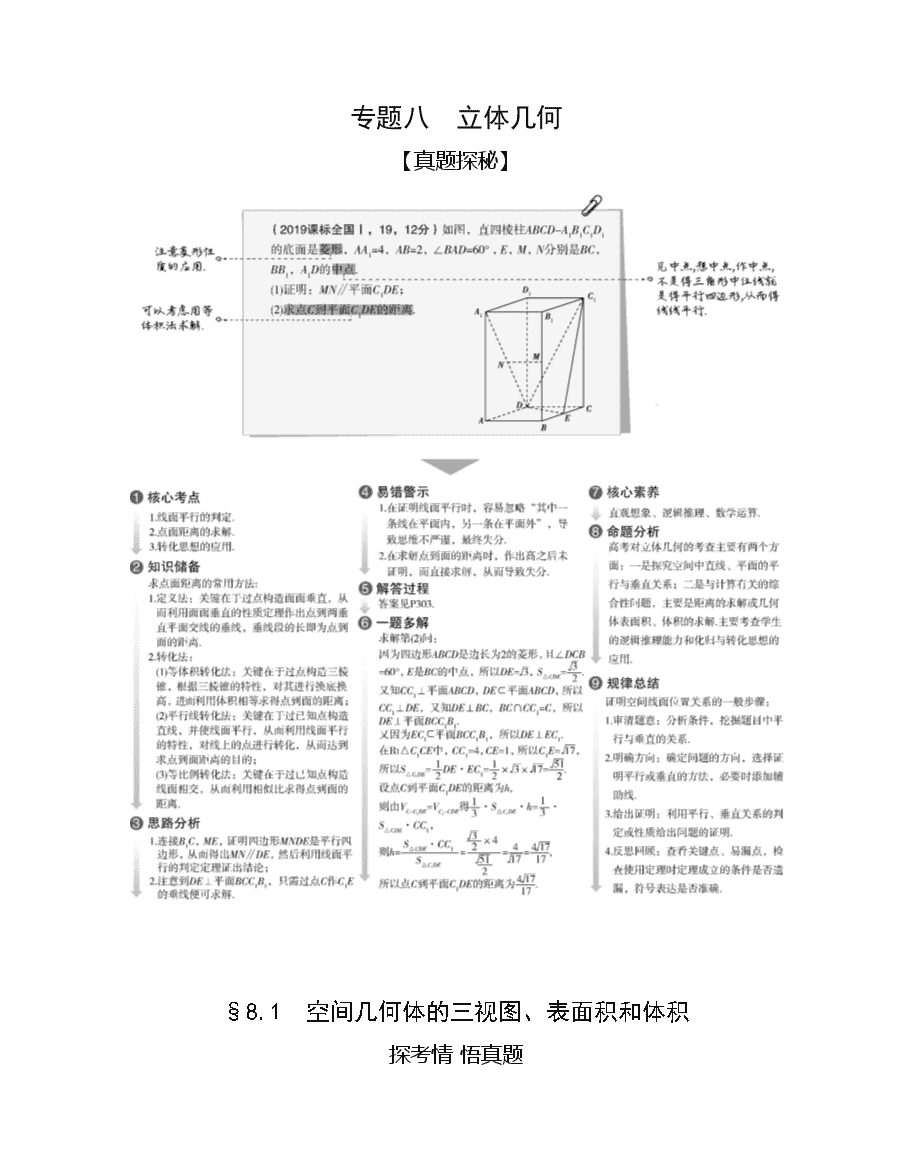
专题八　立体几何 ‎【真题探秘】‎ ‎§8.1　空间几何体的三视图、表面积和体积 探考情 悟真题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 空间几何体的结构及其三视图和直观图 ‎①认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构;②能画出简单空间图形的三视图,能识别三视图所表示的立体模型;会用斜二测画法画出简单几何体的直观图;③会用平行投影与中心投影两种方法画出简单空间图形的三视图和直观图,了解空间图形的不同表示形式 ‎2018课标全国Ⅰ,9,5分 空间几何体的三视图 空间几何体的结构特征及空间几何体表面最短路径问题 ‎★★★‎ ‎2018课标全国Ⅲ,3,5分 空间几何体的三视图 数学文化 ‎2019课标全国Ⅱ,16,5分 空间几何体的结构特征 数学文化 空间几何体的表面积 通过对柱、锥、台、球的研究,掌握柱、锥、台、球的表面积的求法 ‎2018课标全国Ⅰ,5,5分 圆柱的表面积 圆柱的轴截面 ‎★★★‎ ‎2017课标全国Ⅰ,16,5分 三棱锥外接球的表面积 面面垂直的性质定理及三棱锥的体积 ‎2016课标全国Ⅰ,7,5分 球的表面积 空间几何体的三视图 ‎2015课标Ⅰ,11,5分 组合体的表面积 空间几何体的三视图 空间几何体的体积 ‎①理解柱、锥、台体的体积概念;②能运用公式求解柱、锥、台、球的体积,并且熟悉台体、柱体与锥体之间的转换关系 ‎2018课标全国Ⅰ,10,5分 长方体的体积 直线与平面所成角 ‎★★★‎ ‎2017课标全国Ⅱ,6,5分 不规则几何体的体积 空间几何体的三视图 ‎2019课标全国Ⅲ,16,5分 不规则几何体的体积 数学的实际应用,几何体的质量 分析解读 ‎1.理解柱、锥、台、球的概念,牢记它们的几何特征及形成过程.正确把握轴截面、中截面的含义及空间问题转化为平面问题的方法.2.理解三视图的概念及掌握三视图与直观图的画法.3.理解柱、锥、台、球的表面积和体积的概念,掌握其表面积和体积公式.4.高考对本节内容的考查主要以几何体的三视图为背景考查几何体的表面积和体积,分值约为5分,属于中档题.‎ 破考点 练考向 ‎【考点集训】‎ 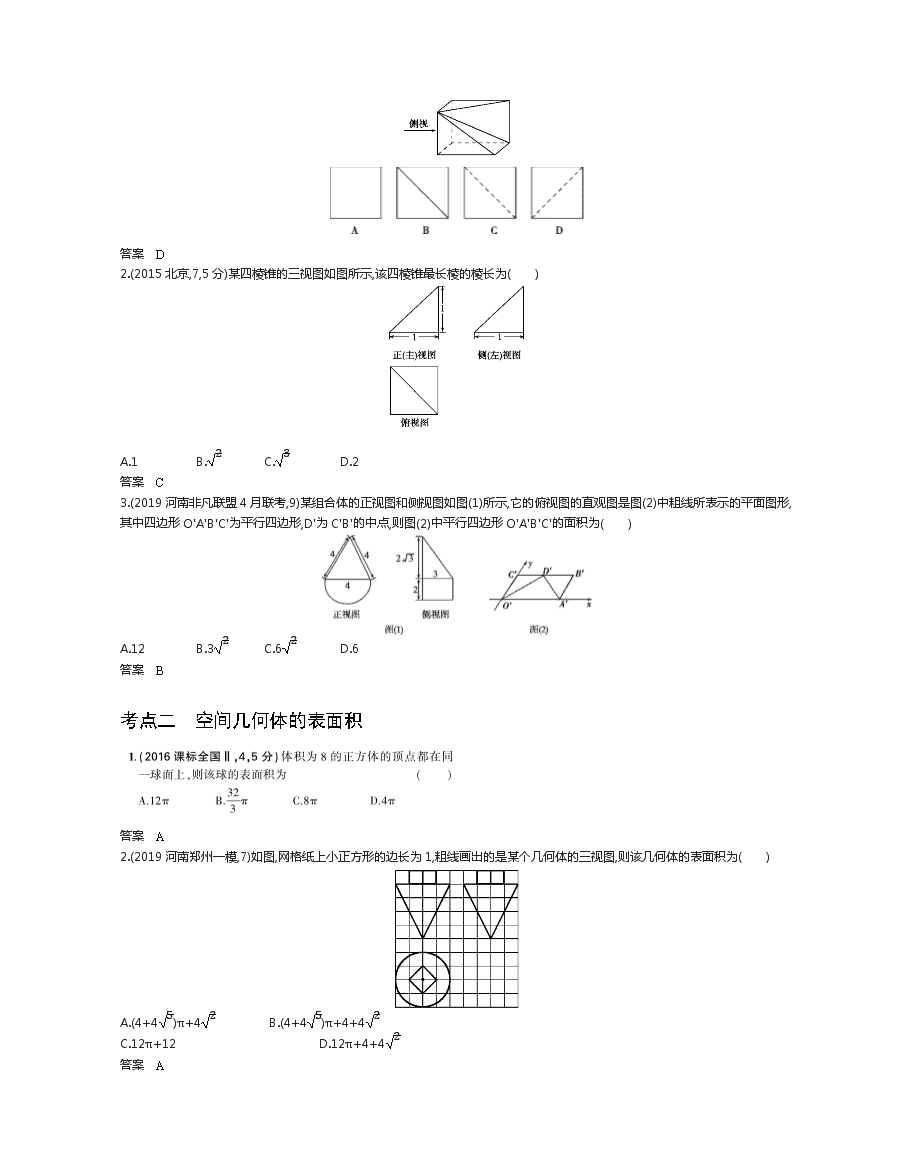考点一　空间几何体的结构及其三视图和直观图 ‎1.(2020届贵州贵阳8月摸底考试,7)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为(　　)‎ 答案　D　‎ ‎2.(2015北京,7,5分)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.1 B.‎2‎ C.‎3‎ D.2‎ 答案　C　‎ ‎3.(2019河南非凡联盟4月联考,9)某组合体的正视图和侧视图如图(1)所示,它的俯视图的直观图是图(2)中粗线所表示的平面图形,其中四边形O'A'B'C'为平行四边形,D'为C'B'的中点,则图(2)中平行四边形O'A'B'C'的面积为(　　)‎ A.12 B.3‎2‎ C.6‎2‎ D.6‎ 答案　B　‎ 考点二　空间几何体的表面积 答案　A　‎ ‎2.(2019河南郑州一模,7)如图,网格纸上小正方形的边长为1,粗线画出的是某个几何体的三视图,则该几何体的表面积为(　　)‎ A.(4+4‎5‎)π+4‎2‎ B.(4+4‎5‎)π+4+4‎‎2‎ C.12π+12 D.12π+4+4‎‎2‎ 答案　A　‎ ‎3.(2020届吉林梅河口五中9月月考,16)已知矩形ABCD的顶点都在半径为5的球O的球面上,且AB=6,BC=2‎5‎,则棱锥O-ABCD的侧面积为　　　　. ‎ 答案　44‎ 考点三　空间几何体的体积 ‎1.(2019江西上饶二模,7)已知下图为某几何体的三视图,则其体积为(　　)‎ A.π+‎2‎‎3‎ B.π+‎1‎‎3‎ C.π+‎4‎‎3‎ D.π+‎‎3‎‎4‎ 答案　C　‎ ‎2.(2018吉林长春质检,8)《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为(　　)‎ A.4立方丈 B.5立方丈 C.6立方丈 D.12立方丈 答案　B　‎ ‎3.(2019天津,12,5分)已知四棱锥的底面是边长为‎2‎的正方形,侧棱长均为‎5‎.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为　　　　. ‎ 答案　‎π‎4‎ 炼技法 提能力 ‎【方法集训】‎ 方法1　空间几何体表面积的求解方法 ‎1.(2016课标全国Ⅱ,7,5分)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.20π B.24π C.28π D.32π 答案　C　‎ ‎2.(2020届湖北部分重点中学9月摸底考试,9)某三棱锥的三视图如图所示,则该棱锥的表面积为(　　)‎ A.‎3‎‎2‎+‎2‎+‎5‎‎2‎ B.‎1‎‎2‎+2‎2‎+‎‎5‎ C.‎1‎‎2‎+‎2‎+‎5‎ D.‎3‎‎2‎+‎2‎+‎‎5‎ 答案　A　‎ ‎3.(2019河南安阳诊断卷,4)某几何体的三视图如图所示,则该几何体的表面积为(　　)‎ A.16+2π B.20+2π C.14+π D.20+π 答案　D　‎ ‎4.(2019广东韶关一调,15)若圆锥与球的体积相等,且圆锥底面半径与球的直径相等,则圆锥侧面积与球的表面积之比为　　　　. ‎ 答案　‎5‎∶2‎ 方法2　空间几何体体积的求解方法 ‎1.(2017北京,6,5分)某三棱锥的三视图如图所示,则该三棱锥的体积为(　　)‎ A.60 B.30 C.20 D.10‎ 答案　D　‎ ‎2.(2019河南顶尖计划联考,9)如图,网格纸中小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为(　　)‎ A.8 B.10 C.20 D.32‎ 答案　C　‎ ‎3.(2018天津,11,5分)如图,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为　　　　. ‎ 答案　‎‎1‎‎3‎ ‎4.(2018江苏,10,5分)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为　　　　. ‎ 答案　‎‎4‎‎3‎ 方法3　与球有关的切、接问题的求解方法 ‎1.(2019宁夏银川质量检测,11)已知直三棱柱ABC-A1B1C1的底面为直角三角形,且两直角边长分别为1和‎3‎,此三棱柱的高为2‎3‎,则该三棱柱的外接球的体积为(　　)‎ A.‎32π‎3‎ B.‎16π‎3‎ C.‎8π‎3‎ D.‎‎64π‎3‎ 答案　A　‎ ‎2.(2016课标全国Ⅲ,11,5分)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是(　　)‎ A.4π B.‎9π‎2‎ C.6π D.‎‎32π‎3‎ 答案　B　‎ ‎3.(2017天津,11,5分)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为　　　　. ‎ 答案　‎9‎‎2‎π ‎4.(2020届湖南顶级名校9月联考,16)正三棱锥P-ABC(底面△ABC为正三角形,顶点P在底面的射影为底面△ABC的中心)中,PA⊥PB,其体积为‎9‎‎2‎,则该三棱锥的外接球的表面积为　　　　. ‎ 答案　27π ‎【五年高考】‎ A组　统一命题·课标卷题组 考点一　空间几何体的结构及其三视图和直观图 ‎1.(2018课标全国Ⅰ,9,5分)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.2‎17‎ B.2‎5‎ C.3 D.2‎ 答案　B　‎ ‎2.(2019课标全国Ⅱ,16,5分)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有　　　　个面,其棱长为　　　　.(本题第一空2分,第二空3分) ‎ 图1‎ 图2‎ 答案　26;‎2‎-1‎ 考点二　空间几何体的表面积 ‎1.(2018课标全国Ⅰ,5,5分)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为(　　)‎ A.12‎2‎π B.12π C.8‎2‎π D.10π 答案　B　‎ ‎2.(2016课标全国Ⅲ,10,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为(　　)‎ A.18+36‎5‎ B.54+18‎‎5‎ C.90 D.81‎ 答案　B　‎ ‎3.(2017课标全国Ⅱ,15,5分)长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为　　　　. ‎ 答案　14π ‎4.(2017课标全国Ⅰ,16,5分)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为　　　　. ‎ 答案　36π 考点三　空间几何体的体积 ‎1.(2018课标全国Ⅰ,10,5分)在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为(　　)‎ A.8 B.6‎2‎ C.8‎2‎ D.8‎‎3‎ 答案　C　‎ ‎2.(2017课标全国Ⅱ,6,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为(　　)‎ A.90π B.63π C.42π D.36π 答案　B　‎ ‎3.(2017课标全国Ⅲ,9,5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为(　　)‎ A.π B.‎3π‎4‎ C.π‎2‎ D.‎π‎4‎ 答案　B　‎ ‎4.(2019课标全国Ⅲ,16,5分)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为　　　　g. ‎ 答案　118.8‎ ‎5.(2018课标全国Ⅱ,16,5分)已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°.若△SAB的面积为8,则该圆锥的体积为　　　　. ‎ 答案　8π ‎6.(2017课标全国Ⅱ,18,12分)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=‎1‎‎2‎AD,∠BAD=∠ABC=90°.‎ ‎(1)证明:直线BC∥平面PAD;‎ ‎(2)若△PCD的面积为2‎7‎,求四棱锥P-ABCD的体积.‎ 答案　(1)证明:在平面ABCD内,‎ 因为∠BAD=∠ABC=90°,‎ 所以BC∥AD.‎ 又BC⊄平面PAD,AD⊂平面PAD,故BC∥平面PAD.‎ ‎(2)取AD的中点M,连接PM,CM.‎ 由AB=BC=‎1‎‎2‎AD及BC∥AD,∠ABC=90°得四边形ABCM为正方形,则CM⊥AD.‎ 因为侧面PAD为等边三角形且垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PM⊥AD,PM⊥底面ABCD.‎ 因为CM⊂底面ABCD,‎ 所以PM⊥CM.‎ 设BC=x,则CM=x,CD=‎2‎x,PM=‎3‎x,PC=PD=2x.‎ 取CD的中点N,连接PN,‎ 则PN⊥CD,所以PN=‎14‎‎2‎x.‎ 因为△PCD的面积为2‎7‎,‎ 所以‎1‎‎2‎×‎2‎x×‎14‎‎2‎x=2‎7‎,‎ 解得x=-2(舍去)或x=2.‎ 于是AB=BC=2,AD=4,PM=2‎3‎.‎ 所以四棱锥P-ABCD的体积V=‎1‎‎3‎×‎2×(2+4)‎‎2‎×2‎3‎=4‎3‎.‎ ‎7.(2016课标全国Ⅱ,19,12分)如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D'EF的位置.‎ ‎(1)证明:AC⊥HD';‎ ‎(2)若AB=5,AC=6,AE=‎5‎‎4‎,OD'=2‎2‎,求五棱锥D'-ABCFE的体积.‎ 答案　(1)证明:由已知得AC⊥BD,AD=CD.‎ 又由AE=CF得AEAD=CFCD,故AC∥EF.(2分)‎ 由此得EF⊥HD,EF⊥HD',所以AC⊥HD'.(4分)‎ ‎(2)由EF∥AC得OHDO=AEAD=‎1‎‎4‎.(5分)‎ 由AB=5,AC=6得DO=BO=AB‎2‎-AO‎2‎=4.‎ 所以OH=1,D'H=DH=3.‎ 于是OD'2+OH2=(2‎2‎)2+12=9=D'H2,故OD'⊥OH.‎ 由(1)知AC⊥HD',又AC⊥BD,BD∩HD'=H,所以AC⊥平面BHD',因为OD'⊂平面BHD',所以AC⊥OD'.‎ 又由OD'⊥OH,AC∩OH=O,所以OD'⊥平面ABC.(8分)‎ 又由EFAC=DHDO得EF=‎9‎‎2‎.‎ 五边形ABCFE的面积S=‎1‎‎2‎×6×8-‎1‎‎2‎×‎9‎‎2‎×3=‎69‎‎4‎.(10分)‎ 所以五棱锥D'-ABCFE的体积V=‎1‎‎3‎×‎69‎‎4‎×2‎2‎=‎23‎‎2‎‎2‎.(12分)‎ B组　自主命题·省(区、市)卷题组 考点一　空间几何体的结构及其三视图和直观图 ‎1.(2019浙江,4,4分)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.158 B.162 C.182 D.324‎ 答案　B　‎ ‎2.(2018北京,6,5分)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(　　)‎ A.1 B.2 C.3 D.4‎ 答案　C　‎ 考点二　空间几何体的表面积 ‎1.(2015福建,9,5分)某几何体的三视图如图所示,则该几何体的表面积等于(　　)‎ A.8+2‎2‎ B.11+2‎2‎ C.14+2‎2‎ D.15‎ 答案　B　‎ ‎2.(2016浙江,9,6分)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是　　　　cm2,体积是　　　　cm3. ‎ 答案　80;40‎ 考点三　空间几何体的体积 ‎1.(2018浙江,3,4分)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是(　　)‎ A.2 B.4 C.6 D.8‎ 答案　C　‎ ‎2.(2016山东,5,5分)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(　　)‎ A.‎1‎‎3‎+‎2‎‎3‎π B.‎1‎‎3‎+‎2‎‎3‎π C.‎1‎‎3‎+‎2‎‎6‎π D.1+‎2‎‎6‎π 答案　C　‎ ‎3.(2019江苏,9,5分)如图,长方体ABCD-A1B1C1D1的体积是120,E为CC1的中点,则三棱锥E-BCD的体积是　　　　. ‎ 答案　10‎ C组　教师专用题组 考点一　空间几何体的结构及其三视图和直观图 ‎1.(2016天津,3,5分)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为(　　)‎ 答案　B　‎ ‎2.(2014课标Ⅰ,8,5分)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱 答案　B　‎ 考点二　空间几何体的表面积 ‎1.(2015课标Ⅰ,11,5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=(　　)‎ A.1 B.2 C.4 D.8‎ 答案　B　‎ ‎2.(2015陕西,5,5分)一个几何体的三视图如图所示,则该几何体的表面积为(　　)‎ A.3π B.4π C.2π+4 D.3π+4‎ 答案　D　‎ ‎3.(2015安徽,9,5分)一个四面体的三视图如图所示,则该四面体的表面积是(　　)‎ A.1+‎3‎ B.1+2‎‎2‎ C.2+‎3‎ D.2‎‎2‎ 答案　C　‎ ‎4.(2014大纲全国,10,5分)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为(　　)‎ A.‎81π‎4‎ B.16π C.9π D.‎‎27π‎4‎ 答案　A　‎ ‎5.(2015课标Ⅱ,10,5分)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为(　　)‎ A.36π B.64π C.144π D.256π 答案　C　‎ ‎6.(2013课标Ⅰ,15,5分)已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为　　　　. ‎ 答案　‎‎9π‎2‎ ‎7.(2013课标Ⅱ,15,5分)已知正四棱锥O-ABCD的体积为‎3‎‎2‎‎2‎,底面边长为‎3‎,则以O为球心,OA为半径的球的表面积为　　　　. ‎ 答案　24π 考点三　空间几何体的体积 ‎1.(2015课标Ⅰ,6,5分)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有(　　)‎ A.14斛 B.22斛 C.36斛 D.66斛 答案　B　‎ ‎2.(2015课标Ⅱ,6,5分)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为(　　)‎ A.‎1‎‎8‎ B.‎1‎‎7‎ C.‎1‎‎6‎ D.‎‎1‎‎5‎ 答案　D　‎ ‎3.(2015浙江,2,5分)某几何体的三视图如图所示(单位:cm),则该几何体的体积是(　　)‎ A.8 cm3 B.12 cm3 C.‎32‎‎3‎ cm3 D.‎40‎‎3‎ cm3‎ 答案　C　‎ ‎4.(2015山东,9,5分)已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为(　　)‎ A.‎2‎2‎π‎3‎ B.‎4‎2‎π‎3‎ C.2‎2‎π D.4‎2‎π 答案　B　‎ ‎5.(2015重庆,5,5分)某几何体的三视图如图所示,则该几何体的体积为(　　)‎ A.‎1‎‎3‎+2π B.‎13π‎6‎ C.‎7π‎3‎ D.‎‎5π‎2‎ 答案　B　‎ ‎6.(2015湖南,10,5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为材料利用率=新工件的体积原工件的体积(　　)‎ A.‎8‎‎9π B.‎8‎‎27π C.‎24(‎2‎-1‎‎)‎‎3‎π D.‎‎8(‎2‎-1‎‎)‎‎3‎π 答案　A　‎ ‎7.(2014课标Ⅱ,6,5分)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为(　　)‎ A.‎17‎‎27‎ B.‎5‎‎9‎ C.‎10‎‎27‎ D.‎‎1‎‎3‎ 答案　C　‎ ‎8.(2013课标Ⅰ,11,5分)某几何体的三视图如图所示,则该几何体的体积为(　　)‎ A.16+8π B.8+8π C.16+16π D.8+16π 答案　A　‎ ‎9.(2012课标全国,7,5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(　　)‎ A.6 B.9 C.12 D.18‎ 答案　B　‎ ‎10.(2012课标全国,8,5分)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为‎2‎,则此球的体积为(　　)‎ A.‎6‎π B.4‎3‎π C.4‎6‎π D.6‎3‎π 答案　B　‎ ‎11.(2010全国Ⅰ,12,5分)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为(　　)‎ A.‎2‎‎3‎‎3‎ B.‎4‎‎3‎‎3‎ C.2‎3‎ D.‎‎8‎‎3‎‎3‎ 答案　B　‎ ‎12.(2017山东,13,5分)由一个长方体和两个‎1‎‎4‎圆柱体构成的几何体的三视图如图,则该几何体的体积为　　　　. ‎ 答案　2+‎π‎2‎ ‎13.(2016四川,12,5分)已知某三棱锥的三视图如图所示,则该三棱锥的体积是　　　　. ‎ 答案　‎‎3‎‎3‎ ‎14.(2016北京,11,5分)某四棱柱的三视图如图所示,则该四棱柱的体积为　　　　. ‎ 答案　‎‎3‎‎2‎ ‎15.(2015天津,10,5分)一个几何体的三视图如图所示(单位:m),则该几何体的体积为　　　　m3. ‎ 答案　‎8‎‎3‎π ‎16.(2011课标,16,5分)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的‎3‎‎16‎,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为　　　　. ‎ 答案　‎‎1‎‎3‎ ‎17.(2015课标Ⅱ,19,12分)如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.‎ ‎(1)在图中画出这个正方形(不必说明画法和理由);‎ ‎(2)求平面α把该长方体分成的两部分体积的比值.‎ 答案　(1)交线围成的正方形EHGF如图:‎ ‎(2)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.‎ 因为EHGF为正方形,所以EH=EF=BC=10.‎ 于是MH=EH‎2‎-EM‎2‎=6,AH=10,HB=6.‎ 因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为‎9‎‎7‎‎7‎‎9‎也正确.‎ ‎18.(2015安徽,19,13分)如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.‎ ‎(1)求三棱锥P-ABC的体积;‎ ‎(2)证明:在线段PC上存在点M,使得AC⊥BM,并求PMMC的值.‎ 答案　(1)由题设AB=1,AC=2,∠BAC=60°,‎ 可得S△ABC=‎1‎‎2‎·AB·AC·sin 60°=‎3‎‎2‎.‎ 由PA⊥平面ABC,可知PA是三棱锥P-ABC的高,又PA=1,‎ 所以三棱锥P-ABC的体积 V=‎1‎‎3‎·S△ABC·PA=‎3‎‎6‎.‎ ‎(2)证明:在平面ABC内,过点B作BN⊥AC,垂足为N.在平面PAC内,过点N作MN∥PA交PC于点M,连接BM.由PA⊥平面ABC知PA⊥AC,所以MN⊥AC.由于BN∩MN=N,故AC⊥平面MBN.又BM⊂平面MBN,所以AC⊥BM.‎ 在直角△BAN中,AN=AB·cos∠BAC=‎1‎‎2‎,从而NC=AC-AN=‎3‎‎2‎.由MN∥PA,得PMMC=ANNC=‎1‎‎3‎.‎ ‎19.(2014江西,19,12分)如图,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1.‎ ‎(1)求证:A1C⊥CC1;‎ ‎(2)若AB=2,AC=‎3‎,BC=‎7‎,问AA1为何值时,三棱柱ABC-A1B1C1体积最大?并求此最大值.‎ 答案　(1)证明:由AA1⊥BC知BB1⊥BC,‎ 又BB1⊥A1B,‎ 故BB1⊥平面BCA1,则BB1⊥A1C,‎ 又BB1∥CC1,‎ 所以A1C⊥CC1.‎ ‎(2)解法一:设AA1=x,‎ 在Rt△A1BB1中,A1B=A‎1‎B‎1‎‎2‎‎-BB‎1‎‎2‎=‎4-‎x‎2‎.‎ 同理,A1C=A‎1‎C‎1‎‎2‎‎-CC‎1‎‎2‎=‎3-‎x‎2‎.‎ 在△A1BC中,cos∠BA1C=‎A‎1‎B‎2‎‎+A‎1‎C‎2‎-BC‎2‎‎2A‎1‎B·A‎1‎C ‎=-x‎2‎‎(4-x‎2‎)(3-x‎2‎)‎,所以sin∠BA1C=‎12-7‎x‎2‎‎(4-x‎2‎)(3-x‎2‎)‎,‎ 所以S‎△A‎1‎BC=‎1‎‎2‎A1B·A1C·sin∠BA1C=‎12-7‎x‎2‎‎2‎.‎ 从而三棱柱ABC-A1B1C1的体积V=S‎△A‎1‎BC·AA1=x‎12-7‎x‎2‎‎2‎.‎ 因为x‎12-7‎x‎2‎=‎12x‎2‎-7‎x‎4‎=‎-7x‎2‎‎-‎‎6‎‎7‎‎2‎+‎‎36‎‎7‎,‎ 故当x=‎6‎‎7‎=‎42‎‎7‎,即AA1=‎42‎‎7‎时,体积V取到最大值‎3‎‎7‎‎7‎.‎ 解法二:过A1作BC的垂线,垂足为D,连接AD.‎ 由于AA1⊥BC,A1D⊥BC,‎ 故BC⊥平面AA1D,BC⊥AD.‎ 又∠BAC=90°,‎ 所以S△ABC=‎1‎‎2‎AD·BC=‎1‎‎2‎AB·AC,得AD=‎2‎‎21‎‎7‎.‎ 设AA1=x,在Rt△AA1D中,‎ A1D=AD‎2‎-AA‎1‎‎2‎=‎12‎‎7‎‎-‎x‎2‎,‎ S‎△A‎1‎BC‎=‎1‎‎2‎A1D·BC=‎12-7‎x‎2‎‎2‎.‎ 从而三棱柱ABC-A1B1C1的体积V=S‎△A‎1‎BC·AA1=x‎12-7‎x‎2‎‎2‎.‎ 因为x‎12-7‎x‎2‎=‎12x‎2‎-7‎x‎4‎=‎-7x‎2‎‎-‎‎6‎‎7‎‎2‎+‎‎36‎‎7‎,‎ 故当x=‎6‎‎7‎=‎42‎‎7‎,即AA1=‎42‎‎7‎时,体积V取到最大值‎3‎‎7‎‎7‎.‎ ‎20.(2013课标Ⅱ,18,12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.‎ ‎(1)证明:BC1∥平面A1CD;‎ ‎(2)设AA1=AC=CB=2,AB=2‎2‎,求三棱锥C-A1DE的体积.‎ 答案　(1)证明:连接AC1交A1C于点F,‎ 则F为AC1中点.‎ 由D是AB中点,连接DF,则BC1∥DF.‎ 因为DF⊂平面A1CD,BC1⊄平面A1CD,‎ 所以BC1∥平面A1CD.‎ ‎(2)因为ABC-A1B1C1是直三棱柱,‎ 所以AA1⊥CD.由已知AC=CB,D为AB的中点,‎ 所以CD⊥AB.‎ 又AA1∩AB=A,于是CD⊥平面ABB1A1.‎ 由AA1=AC=CB=2,AB=2‎2‎得 ‎∠ACB=90°,CD=‎2‎,A1D=‎6‎,DE=‎3‎,A1E=3,‎ 故A1D2+DE2=A1E2,即DE⊥A1D.‎ 所以VC-A‎1‎DE=‎1‎‎3‎×‎1‎‎2‎×‎6‎×‎3‎×‎2‎=1.‎ ‎【三年模拟】‎ 时间:50分钟　分值:60分 一、选择题(每小题5分,共45分)‎ ‎1.(2018广东佛山一模,9)某几何体的三视图如图所示,则该几何体的体积为(　　)‎ A.‎21‎‎2‎ B.15 C.‎33‎‎2‎ D.18‎ 答案　C　‎ ‎2.(2020届河南顶级名校摸底考试,6)在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,若某个鳖臑的三视图均是直角边长为1的等腰直角三角形(如图所示),则该鳖臑表面中最大面的面积为(　　)‎ A.‎2‎‎2‎ B.1 C.‎2‎ D.1+‎‎2‎ 答案　A　‎ ‎3.(2019全国大联考,8)已知半球O的半径r=2,正三棱柱ABC-A1B1C1内接于半球O,其中底面ABC在半球O的大圆面内,点A1,B1,C1在半球O的球面上.若正三棱柱ABC-A1B1C1的侧面积为6‎3‎,则其侧棱的长是(　　)‎ A.‎6‎ B.2 C.‎3‎ D.‎‎2‎ 答案　D　‎ ‎4.(2020届安徽A10联盟摸底考试,10)某几何体的三视图如图所示,则该几何体的体积为(　　)‎ A.‎2‎‎3‎ B.‎4‎‎3‎ C.2 D.4‎ 答案　B　‎ ‎5.(2019安徽黄山模拟,9)某三棱锥的三视图如图所示,则该三棱锥内切球的表面积为(　　)‎ A.(12-8‎2‎)π B.(12-6‎2‎)π C.(10-6‎2‎)π D.(8-4‎2‎)π 答案　A　‎ ‎6.(2019江西九江一模,8)如图,网格纸上小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为(　　)‎ A.‎4‎‎3‎ B.‎8‎‎3‎ C.4 D.‎‎16‎‎3‎ 答案　D　‎ ‎7.(2020届百师联盟开学摸底考试,12)在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA⊥底面ABCD,异面直线AC与PD所成的角的余弦值为‎10‎‎5‎,则四棱锥外接球的表面积为(　　)‎ A.48π B.12π C.36π D.9π 答案　D　‎ ‎8.(2020届西北工大附中9月月考,9)在三棱锥P-ABC中,平面PAB⊥平面ABC,△ABC是斜边AB=2‎3‎的直角三角形,PA=PB=‎7‎,则三棱锥外接球的表面积为(　　)‎ A.16π B.‎65π‎4‎ C.‎65π‎16‎ D.‎‎49π‎4‎ 答案　D　‎ ‎9.(2018云南玉溪一中期中,11)已知三棱锥P-ABC的各顶点都在同一球面上,且PA⊥平面ABC,若该三棱锥的体积为‎2‎‎3‎‎3‎,AB=2,AC=1,∠BAC=60°,则球的表面积等于(　　)‎ A.5π B.20π C.8π D.16π 答案　B　‎ 二、填空题(每小题5分,共15分)‎ ‎10.(2018陕西部分重点中学摸底检测,14)把边长为1的正方形ABCD沿对角线BD折起,使得平面ABD⊥平面CBD,形成的三棱锥C-ABD的正视图与俯视图如图所示,则侧视图的面积为　　　　. ‎ 答案　‎‎1‎‎4‎ ‎11.(2020届广西桂林十八中9月月考,16)已知球的直径DC=4,A,B是球面上的两点,∠ADC=∠BDC=π‎6‎,则三棱锥A-BCD的体积的最大值是　　　　. ‎ 答案　2‎ ‎12.(2020届广西柳州重点中学摸底考试,15)菱形ABCD的边长为6,∠BAD=60°,将△BCD沿对角线BD翻折,使得二面角C-BD-A的大小为120°,已知A、B、C、D四点在同一球面上,则球的表面积等于　　　　. ‎ 答案　84π