高考文科数学专题复习练习3系统抽样 7页

‎148‎ 系统抽样 ‎14.(2015辽宁大连一模,文14,系统抽样,填空题)将高一(9)班参加社会实践编号分别为:1,2,3,…,48的48名学生,采用系统抽样的方法抽取一个容量为4的样本,已知5号,29号,41号学生在样本中,则样本中还有一名学生的编号是　　　　　. ‎ 解析:样本间距为48÷4=12,则另外一个编号为5+12=17.‎ 答案:17‎ ‎149‎ 分层抽样 ‎14.(2015辽宁大连二模,文14,分层抽样,填空题)某个年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为　　　　　. ‎ 解析:∵有男生560人,女生420人,‎ ‎∴年级共有560+420=980人.‎ ‎∵用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,‎ ‎∴每个个体被抽到的概率是‎280‎‎980‎‎=‎‎2‎‎7‎.‎ ‎∴要从男生中抽取560×‎2‎‎7‎=160.‎ 答案:160‎ ‎9.(2015天津河北区一模,文9,分层抽样,填空题)某高校甲、乙、丙、丁四个专业分别有150,150,400,300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为　　　　　. ‎ 解析:∵甲、乙、丙、丁四个专业分别有150,150,400,300名学生,‎ ‎∴共有学生150+150+400+300=1 000(人).‎ ‎∵用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,‎ ‎∴每个个体被抽到的概率是‎40‎‎1 000‎‎=‎‎1‎‎25‎.‎ ‎∵丙专业有400人,∴要抽取400×‎1‎‎25‎=16(人).‎ 答案:16‎ ‎150‎ 频率分布直方图 ‎13.(2015辽宁锦州一模,文13,频率分布直方图,填空题)如图所示是某公司(共有员工300人)2015年员工年薪情况的频率分布直方图,由此可知,员工中年薪在1.4万元~1.6万元之间的共有　　　　　人. ‎ 解析:由所给图形,可知员工中年薪在1.4万元~1.6万元之间的频率为1-(0.02+0.08+0.08+0.10+0.10)×2=0.24.‎ 所以年薪在1.4万元~1.6万元之间的共有300×0.24=72人.‎ 答案:72‎ ‎14.(2015河南郑州一模,文14,频率分布直方图,填空题)某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15,则该班的学生人数是　　　　　. 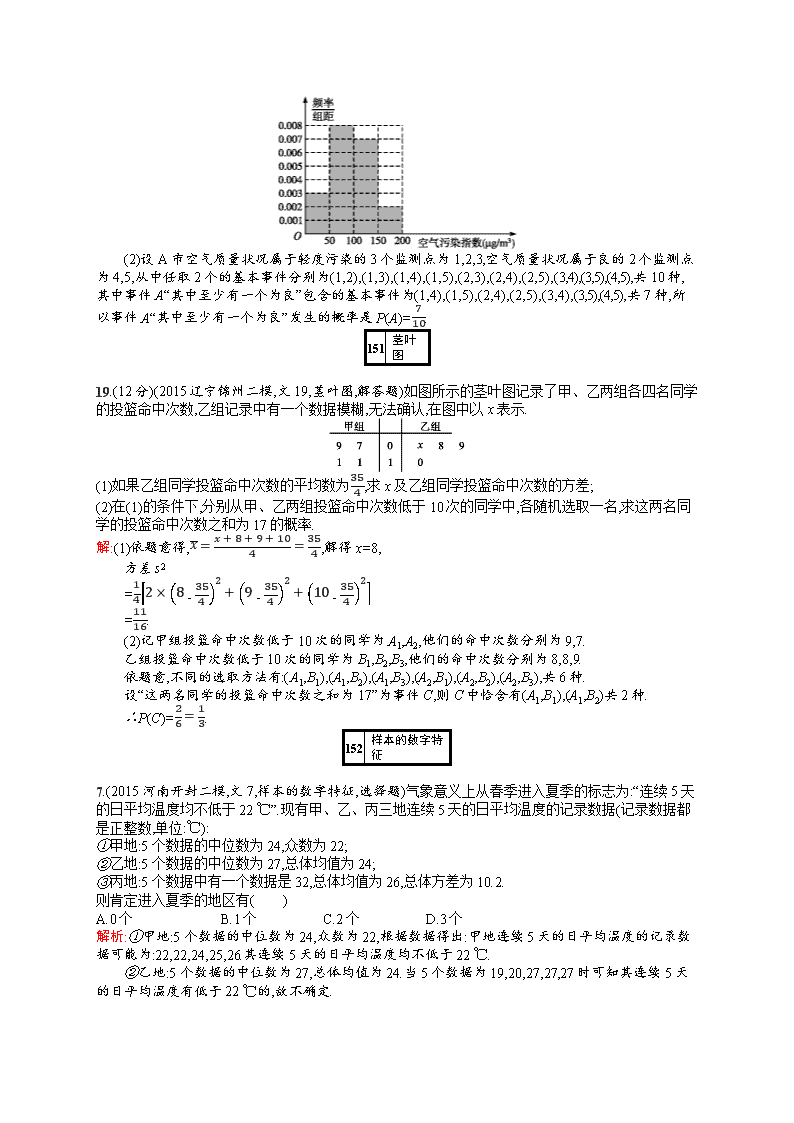‎ 解析:∵成绩低于60分有第一、二组数据,在频率分布直方图中,对应矩形的高分别为0.005,0.010,每组数据的组距为20,则成绩低于60分的频率P=(0.005+0.010)×20=0.3.‎ 又∵低于60分的人数是15,则该班的学生人数是‎15‎‎0.3‎=50.‎ 答案:50‎ ‎18.(12分)(2015哈尔滨师大附中、东北师大附中、辽宁省实验中学一模,文18,频率分布直方图,解答题)空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:‎ 空气污染指数 ‎(单位:μg/m3)‎ ‎[0,50]‎ ‎(50,100]‎ ‎(100,150]‎ ‎(150,200]‎ 监测点个数 ‎15‎ ‎40‎ y ‎10‎ ‎(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;‎ ‎(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?‎ 解:(1)根据频率分布直方图,‎ 得0.003×50=‎15‎x,∴x=100.‎ 又∵15+40+y+10=100,∴y=35.‎ ‎∴直方图中(50,100]对应矩形的高为‎40‎‎100×50‎=0.008,(100,150]对应矩形的高为‎35‎‎100×50‎=0.007,(150,200]对应矩形的高为‎10‎‎100×50‎=0.002.‎ 补全频率分布直方图,如图所示.‎ ‎(2)设A市空气质量状况属于轻度污染的3个监测点为1,2,3,空气质量状况属于良的2个监测点为4,5,从中任取2个的基本事件分别为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10种,其中事件A“其中至少有一个为良”包含的基本事件为(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),(4,5),共7种,所以事件A“其中至少有一个为良”发生的概率是P(A)=‎7‎‎10‎.‎ ‎151‎ 茎叶图 ‎19.(12分)(2015辽宁锦州二模,文19,茎叶图,解答题)如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中以x表示.‎ ‎(1)如果乙组同学投篮命中次数的平均数为‎35‎‎4‎,求x及乙组同学投篮命中次数的方差;‎ ‎(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为17的概率.‎ 解:(1)依题意得,x‎=x+8+9+10‎‎4‎=‎‎35‎‎4‎,解得x=8,‎ 方差s2‎ ‎=‎‎1‎‎4‎‎2×‎8-‎‎35‎‎4‎‎2‎+‎9-‎‎35‎‎4‎‎2‎+‎‎10-‎‎35‎‎4‎‎2‎ ‎=‎11‎‎16‎.‎ ‎(2)记甲组投篮命中次数低于10次的同学为A1,A2,他们的命中次数分别为9,7.‎ 乙组投篮命中次数低于10次的同学为B1,B2,B3,他们的命中次数分别为8,8,9.‎ 依题意,不同的选取方法有:(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),共6种.‎ 设“这两名同学的投篮命中次数之和为17”为事件C,则C中恰含有(A1,B1),(A1,B2)共2种.‎ ‎∴P(C)=‎2‎‎6‎‎=‎‎1‎‎3‎.‎ ‎152‎ 样本的数字特征 ‎7.(2015河南开封二模,文7,样本的数字特征,选择题)气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于22 ℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数,单位:℃):‎ ‎①甲地:5个数据的中位数为24,众数为22;‎ ‎②乙地:5个数据的中位数为27,总体均值为24;‎ ‎③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.2.‎ 则肯定进入夏季的地区有(　　)‎ A.0个 B.1个 C.2个 D.3个 解析:①甲地:5个数据的中位数为24,众数为22,根据数据得出:甲地连续5天的日平均温度的记录数据可能为:22,22,24,25,26.其连续5天的日平均温度均不低于22 ℃.‎ ‎②乙地:5个数据的中位数为27,总体均值为24.当5个数据为19,20,27,27,27时可知其连续5天的日平均温度有低于22 ℃的,故不确定.‎ ‎③丙地:5个数据中有一个数据是32,总体均值为26,若有低于22,则取21,此时方差就超出了10.2,可知其连续5天的日平均温度均不低于22 ℃.‎ 则肯定进入夏季的地区有甲、丙三地.‎ 答案:C ‎155‎ 回归方程的求法及回归分析 ‎13.(2015辽宁锦州二模,文13,回归方程的求法及回归分析,填空题)已知下列表格所示的数据的回归直线方程为y‎^‎=3.8x+a,则a的值为　　　　　. ‎ x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎251‎ ‎254‎ ‎257‎ ‎262‎ ‎266‎ 解析:由表格可知,样本中心点的横坐标为:‎2+3+4+5+6‎‎5‎=4,纵坐标为:‎251+254+257+262+266‎‎5‎=258.‎ 由回归直线经过样本中心点,所以258=3.8×4+a,a=242.8.‎ 答案:242.8‎ ‎7.(2015辽宁大连二模,文7,回归方程的求法及回归分析,选择题)对于下列表格所示五个散点,已知求得的线性回归直线方程为y‎^‎=0.8x-155,则实数m的值为(　　)‎ x ‎196‎ ‎197‎ ‎200‎ ‎203‎ ‎204‎ y ‎1‎ ‎3‎ ‎6‎ ‎7‎ m A.8 B.8.2 C.8.4 D.8.5‎ 解析:由题意,x‎=‎‎1‎‎5‎(196+197+200+203+204)=200,‎ y‎=‎‎1‎‎5‎‎(1+3+6+7+m)=‎17+m‎5‎,‎ 代入y‎^‎=0.8x-155,可得‎17+m‎5‎=0.8×200-155,m=8.‎ 答案:A ‎156‎ 独立性检验 ‎18.(12分)(2015辽宁沈阳一模,文18,独立性检验,解答题)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表所示.‎ 参加社团活动 不参加社团活动 合计 学习积极性高 ‎17‎ ‎8‎ ‎25‎ 学习积极性一般 ‎5‎ ‎20‎ ‎25‎ 合计 ‎22‎ ‎28‎ ‎50‎ ‎(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?‎ ‎(2)试运用独立性检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.‎ K2=n(ad-bc‎)‎‎2‎‎(a+b)(c+d)(a+c)(b+d)‎.‎ P(K2≥k0)‎ ‎0.05‎ ‎0.01‎ ‎0.001‎ k0‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ 解:(1)参加社团活动的学生有22人,总人数为50人,所以随机从该班抽查一名学生,抽到参加社团活动的学生的概率是‎22‎‎50‎‎=‎‎11‎‎25‎.‎ 不参加社团活动且学习积极性一般的学生为20人,所以其概率为‎20‎‎50‎‎=‎‎2‎‎5‎.‎ ‎(2)K2的观测值为k=‎50×(17×20-5×8‎‎)‎‎2‎‎22×28×25×25‎≈11.7,‎ ‎∵k>10.828,∴有99.9%的把握认为学生的学习积极性与参加社团活动情况有关系.‎ ‎18.(12分)(2015辽宁重点中学协作体模拟,文18,独立性检验,解答题)为了研究“教学方式”对教学质量的影响,某校数学老师分别用两种不同的教学方式对入学时数学平均分数和优秀率都相同的甲、乙两个班级进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.‎ ‎(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学中至少有一名被抽中的概率;‎ ‎(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断是否有99%的把握认为“成绩优秀与教学方式有关”.‎ 甲班 乙班 合计 优秀 不优秀 合计 下面临界值表仅供参考:‎ P(K2≥k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 参考公式:K2=n(ad-bc‎)‎‎2‎‎(a+b)(c+d)(a+c)(b+d)‎.‎ 解:(1)记成绩为87分的同学为A,B,其他不低于80分的同学为C,D,E,“从甲班数学成绩不低于80分的同学中随机抽取两名同学”的一切可能结果组成的基本事件有:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E),共10个,‎ ‎“抽到至少有一个87分的同学”所组成的基本事件有:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),一共7个,所以所求事件的概率是P=‎7‎‎10‎.‎ ‎(2)‎ 甲班 乙班 合计 优秀 ‎6‎ ‎14‎ ‎20‎ 不优秀 ‎14‎ ‎6‎ ‎20‎ 合计 ‎20‎ ‎20‎ ‎40‎ K2的观测值k=‎40×(6×6-14×14‎‎)‎‎2‎‎20×20×20×20‎=6.400<6.635.‎ 因此,我们没有99%的把握认为成绩优秀与教学方式有关.‎ ‎18.(12分)(2015河南商丘一模,文18,独立性检验,解答题)为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500 mL以上为常喝,体重超过50 kg为肥胖.‎ 常喝 不常喝 合计 肥胖 ‎2‎ 不肥胖 ‎18‎ 合计 ‎30‎ 已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为‎4‎‎15‎.‎ ‎(1)请将上面的列联表补充完整;‎ ‎(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;‎ ‎(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少?‎ 参考数据:‎ P(K2>k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎　‎‎　‎参考公式:K2=n(ad-bc‎)‎‎2‎‎(a+b)(c+d)(a+c)(b+d)‎,其中n=a+b+c+d‎　‎‎　‎ 解:(1)设常喝碳酸饮料肥胖的学生有x人,x+2‎‎30‎‎=‎‎4‎‎15‎,‎ ‎∴x=6.‎ 常喝 不常喝 合计 肥胖 ‎6‎ ‎2‎ ‎8‎ 不肥胖 ‎4‎ ‎18‎ ‎22‎ 合计 ‎10‎ ‎20‎ ‎30‎ ‎(2)由已知数据可求得:K2的观测值 k=‎30×(6×18-2×4‎‎)‎‎2‎‎10×20×8×22‎≈8.522>7.879,‎ 因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.‎ ‎(3)设常喝碳酸饮料的肥胖者男生为A,B,C,D,女生为E,F,则任取两人有AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15种.‎ 其中一男一女有AE,AF,BE,BF,CE,CF,DE,DF.‎ 故抽出一男一女的概率是P=‎8‎‎15‎.‎ ‎19.(12分)(2015河南中原名校联盟模拟,文19,独立性检验,解答题)2015年3月份全国两会召开后,中国足球引起重视,某校对学生是否喜欢足球进行了抽样调查,男女生各抽了50名,相关数据如下表所示:‎ 不喜欢足球 喜欢足球 总计 男生 ‎18‎ ‎32‎ ‎50‎ 女生 ‎34‎ ‎16‎ ‎50‎ 总计 ‎52‎ ‎48‎ ‎100‎ ‎(1)用分层抽样的方法在喜欢足球的学生中随机抽取6名,男生应该抽取几名?‎ ‎(2)在上述抽取的6名学生中任取2名,求恰有1名女生的概率.‎ ‎(3)能否在犯错误的概率不超过0.005的前提下认为性别与喜欢足球有关系?‎ 参考公式及数据:K2=n(ad-bc‎)‎‎2‎‎(a+b)(c+d)(a+c)(b+d)‎,其中n=a+b+c+d.‎ P(K≥k0)‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 解:(1)喜欢足球的学生有48人,随机抽取6名,男生应该抽取32×‎6‎‎48‎=4人.‎ ‎(2)随机抽取6名,有4名男生,2名女生,任取2名,共有C‎6‎‎2‎=15种方法,恰有1名女生有4×2=8种方法,‎ ‎∴恰有1名女生的概率为‎8‎‎15‎.‎ ‎(3)K2的观测值k=‎‎100×(18×16-32×34‎‎)‎‎2‎‎50×50×48×52‎ ‎≈10.256>7.879,‎ ‎∴在犯错误的概率不超过0.005的前提下认为性别与喜欢足球有关系.‎