高中数学必修2全册同步检测：2-2-3 8页

‎2-2-3‎直线与平面平行的性质 一、选择题 ‎1．已知直线a、b、c及平面α，下列哪个条件能确定a∥b(　　)‎ A．a∥α，b∥α　　　　　 B．a⊥c，b⊥c C．a、b与c成等角 D．a∥c，b∥c ‎2．正方体ABCD－A1B‎1C1D1中，截面BA‎1C1与直线AC的位置关系是(　　)‎ A．AC∥截面BA‎1C1 B．AC与截面BA‎1C1相交 C．AC在截面BA‎1C1内 D．以上答案都错误 ‎3．已知直线l∥平面α，l⊂平面β，α∩β＝m，则直线l，m的位置关系是(　　)‎ A．相交 B．平行 C．异面 D．相交或异面 ‎4．已知直线m∥直线n，直线m∥平面α，过m的平面β与α相交于直线a，则n与a的位置关系是(　　)‎ A．平行 B．相交 C．异面 D．以上均有可能 ‎5．设a，b是两条直线，α，β是两个平面，若a∥α，a⊂β，α∩β＝b，则α内与b相交的直线与a的位置关系是(　　)‎ A．平行 B．相交 C．异面 D．平行或异面 ‎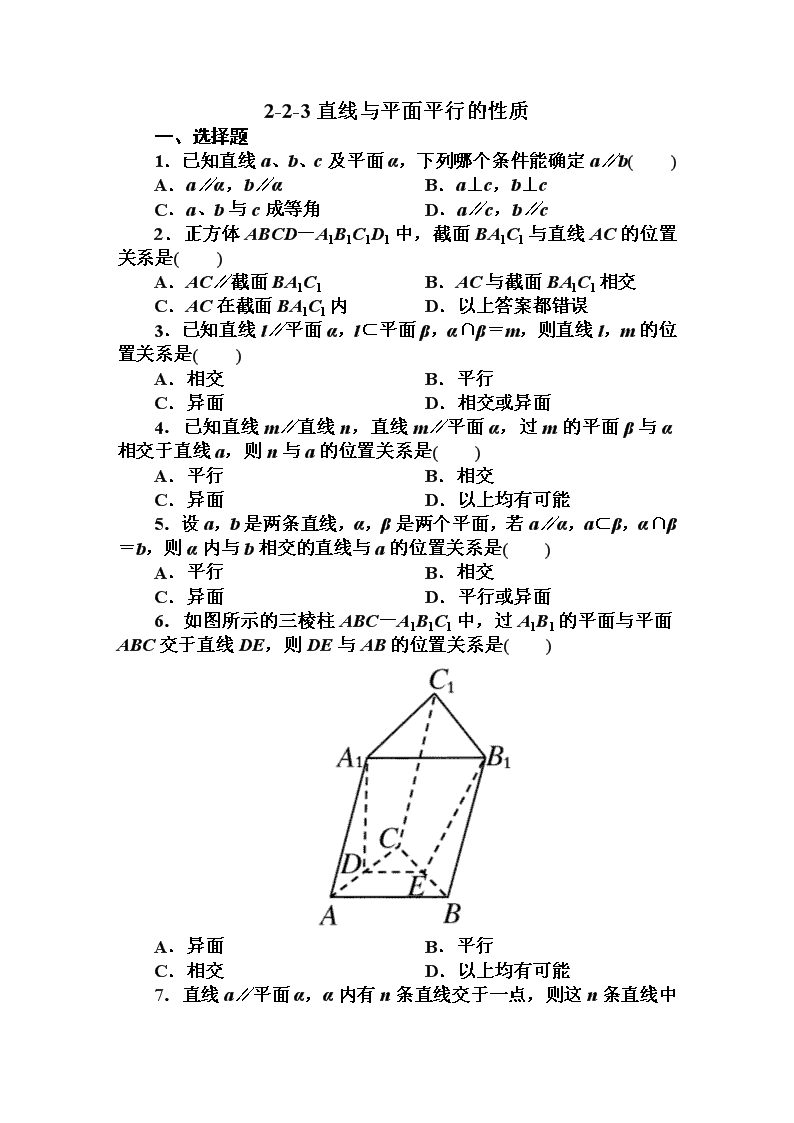6．如图所示的三棱柱ABC－A1B‎1C1中，过A1B1的平面与平面ABC交于直线DE，则DE与AB的位置关系是(　　)‎ A．异面 B．平行 C．相交 D．以上均有可能 ‎7．直线a∥平面α，α内有n条直线交于一点，则这n 条直线中与直线a平行的直线(　　)‎ A．至少有一条 B．至多有一条 C．有且只有一条 D．没有 ‎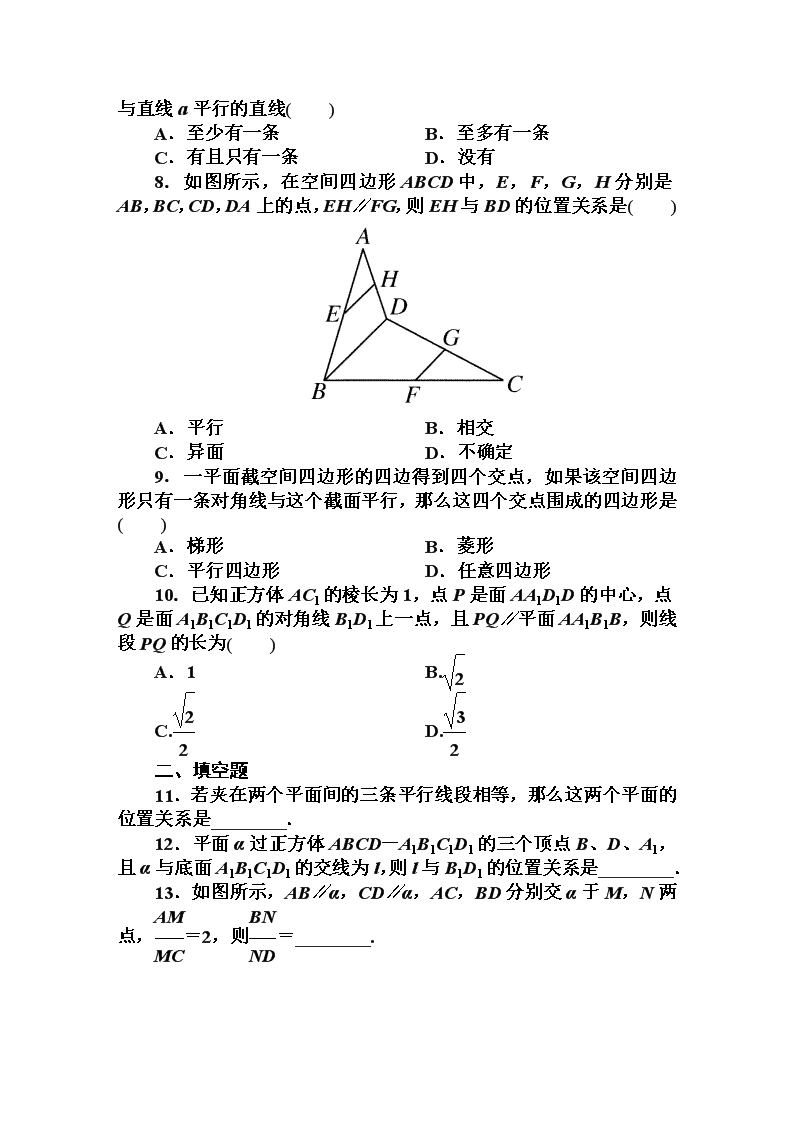8．如图所示，在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，EH∥FG，则EH与BD的位置关系是(　　)‎ A．平行 B．相交 C．异面 D．不确定 ‎9．一平面截空间四边形的四边得到四个交点，如果该空间四边形只有一条对角线与这个截面平行，那么这四个交点围成的四边形是(　　)‎ A．梯形 B．菱形 C．平行四边形 D．任意四边形 ‎10．已知正方体AC1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B‎1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，则线段PQ的长为(　　)‎ A．1 B. C. D. 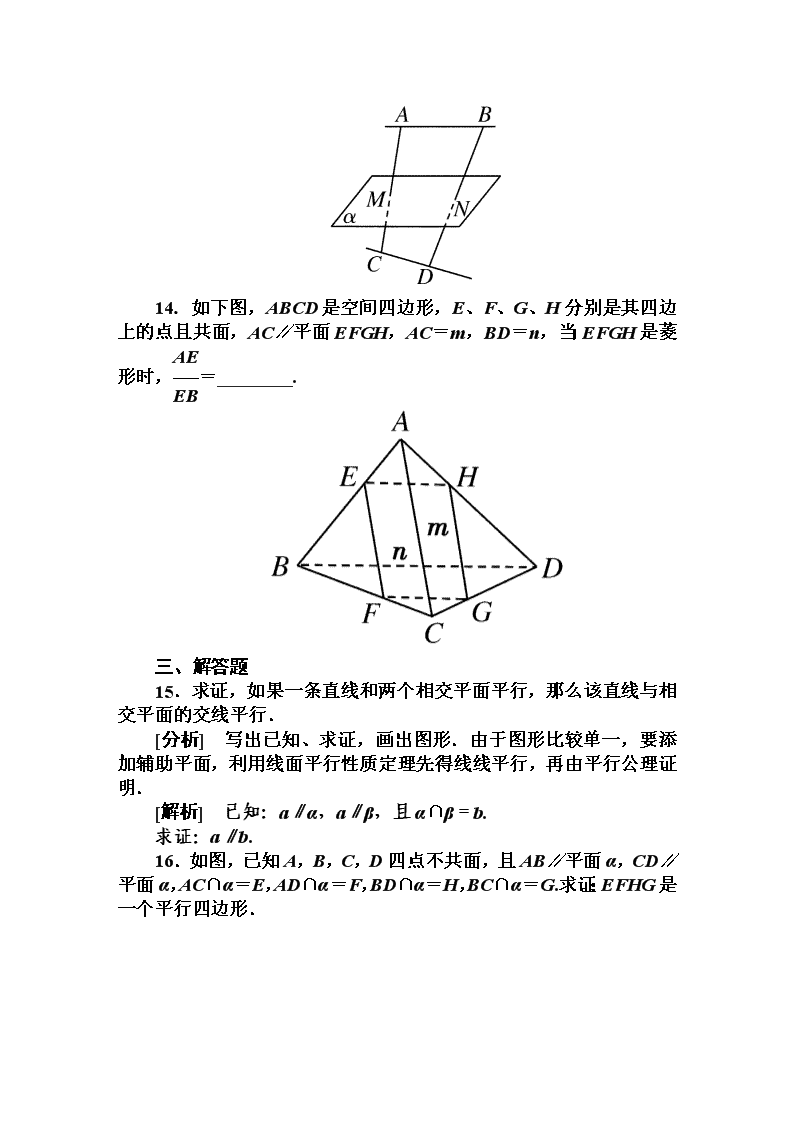二、填空题 ‎11．若夹在两个平面间的三条平行线段相等，那么这两个平面的位置关系是________．‎ ‎12．平面α过正方体ABCD－A1B‎1C1D1的三个顶点B、D、A1，且α与底面A1B‎1C1D1的交线为l，则l与B1D1的位置关系是________．‎ ‎13．如图所示，AB∥α，CD∥α，AC，BD分别交α于M，N两点，＝2，则＝________.‎ ‎14．如下图，ABCD是空间四边形，E、F、G、H分别是其四边上的点且共面，AC∥平面EFGH，AC＝m，BD＝n，当EFGH是菱形时，＝________.‎ 三、解答题 ‎15．求证，如果一条直线和两个相交平面平行，那么该直线与相交平面的交线平行．‎ ‎[分析]　写出已知、求证，画出图形．由于图形比较单一，要添加辅助平面，利用线面平行性质定理先得线线平行，再由平行公理证明．‎ ‎[解析]　已知：a∥α，a∥β，且α∩β＝b.‎ 求证：a∥b.‎ ‎16．如图，已知A，B，C，D四点不共面，且AB∥平面α，CD∥平面α，AC∩α＝E，AD∩α＝F，BD∩α＝H，BC∩α＝G.求证：EFHG是一个平行四边形．‎ ‎17．如下图，在长方体ABCD－A1B‎1C1D1中，E、H分别是棱A1B1、D‎1C1上的点，且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F、G.‎ 求证：FG∥平面ADD‎1A1.‎ ‎18．四棱锥P－ABCD的底面ABCD是梯形，AB∥CD，且AB＝CD.试问在PC上能否找到一点E，使得BE∥平面PAD？若能，请确定E点的位置，并给出证明；若不能，请说明理由．‎ 详解答案 ‎1[答案]　D ‎2[答案]　A ‎[解析]　∵AC∥A‎1C1，‎ 又∵AC⊄面BA‎1C1，‎ ‎∴AC∥面BA‎1C1.‎ ‎3[答案]　B ‎[解析]　这是线面平行性质定理的条件，则l∥m.‎ ‎4[答案]　A ‎[解析]　∵m∥α，α∩β＝a，m⊂β，‎ ‎∴m∥a.又m∥n，∴n∥a.‎ ‎5[答案]　C ‎[解析]　∵a∥α，a⊂β，α⊂β＝b，‎ ‎∴a∥b.‎ ‎∴α内与b相交的直线与a异面．‎ ‎6[答案]　B ‎[解析]　∵A1B1∥AB，AB⊂平面ABC，A1B1⊄ABC，‎ ‎∴A1B1∥平面ABC.‎ 又A1B1⊂平面A1B1ED，平面A1B1ED∩平面ABC＝DE，∴DE∥A1B1.‎ 又AB∥A1B1，∴DE∥AB.‎ ‎7[答案]　B ‎[解析]　设这n条直线的交点为P，则点P不在直线a上，那么直线a和点P确定一个平面β，则点P既在平面α内又在平面β内，则平面α与平面β相交．设交线为直线b，则直线b过点P.又直线a∥平面α，a⊂平面β，则a∥b.很明显这样作出的直线b有且只有一条，‎ 那么直线b可能在这n条直线中，也可能不在，即这n条直线中与直线a平行的直线至多有一条．‎ ‎8[答案]　A ‎[解析]　∵EH∥FG，FG⊂平面BCD，EH⊄平面BCD，‎ ‎∴EH∥平面BCD.‎ ‎∵EH⊂平面ABD，平面ABD∩平面BCD＝BD，‎ ‎∴EH∥BD.‎ ‎9[答案]　A ‎[解析]　由性质定理得截面四边形有一组对边平行．‎ ‎10[答案]　C ‎[解析]　由PQ∥平面AA1BB知PQ∥AB1，又P为AO1的中点，∴PQ＝AB1＝.‎ ‎11[答案]　平行或相交 ‎12[答案]　平行 ‎13[答案]　2‎ ‎[解析]　如图，连接AD交平面α于E点，连接ME和NE.‎ ‎∵平面ACD∩α＝ME，CD∥α，CD⊂平面ACD，‎ ‎∴CD∥ME.∴＝.‎ 同理，＝，‎ ‎∴＝.‎ ‎∴＝2.‎ ‎14[答案]　 ‎[解析]　＝＝＝，而EF＝FG.‎ ‎15证明：如图，在平面α上任取一点A，且使A∉b.∵a∥α，∴A∉a.‎ 故点A和直线a确定一个平面γ，设γ∩α＝m.‎ 同理，在平面β上任取一点B，且使B∉b，‎ 则B和a确定平面δ，设δ∩β＝n.‎ ‎∵a∥α，a⊂γ，γ∩α＝m，∴a∥m.‎ 同理a∥n，则m∥n.‎ 又m⊄β，n⊂β，∴m∥β.‎ 又∵m⊂α，α∩β＝b，∴m∥b.又a∥m，∴a∥b.‎ ‎[点评]　本题利用线面平行的判定和性质定理，完成了平面问题和空间问题的相互转化．转化的思想是一种重要的数学思想．本节常用的转化为：‎ ‎16[证明]　∵AB∥α，平面ABC∩α＝EG，AB⊂平面ABC，∴EG∥AB.‎ 同理，FH∥AB，∴EG∥FH.‎ 同理，EF∥GH.‎ ‎∴四边形EFHG是一个平行四边形．‎ ‎17[证明]　∵EH∥A1D1，又A1D1∥B‎1C1‎ ‎∴EH∥B‎1C1‎ ‎∴EH∥平面BCC1B1‎ 又平面EHGF∩平面BCC1B1＝FG ‎∴EH∥FG　∴FG∥A1D1　又FG⊄平面ADD‎1A，A1D1⊂平面ADD‎1A1，‎ ‎∴FG∥平面ADD‎1A1.‎ ‎18[解析]　在PC上取点E，使＝，‎ 则BE∥平面PAD.‎ 证明如下：延长DA和CB交于点F，连接PF.‎ 梯形ABCD中，AB∥CD，AB＝CD.‎ ‎∴＝＝，‎ ‎∴＝.‎ 又＝，‎ ‎∴△PFC中，＝，‎ ‎∴BE∥PF，‎ 而BE⊄平面PAD，PF⊂平面PAD.‎ ‎∴BE∥平面PAD. ‎