【数学】2019届一轮复习人教A版第8章立体几何初步第2课时直线与平面的位置学案 11页

第2课时　直线与平面的位置 ‎ 关系(1) (对应学生用书(文)109 110页、(理)111 112页)‎ 了解直线与平面的位置关系，了解线面平行的有关概念；除了能熟练运用线面平行的判定定理和性质定理外，还能运用定义判断位置关系．‎ ‎① 要熟练掌握线面平行的定义、判定及性质.② 要注意线线关系、线面关系以及面面关系的转化．对于直线与平面所成的角，点到面的距离了解即可．‎ ‎1. (必修2P35练习2改编)给出下列条件：① l∥α；② l与α至少有一个公共点；③ l与α至多有一个公共点．则能确定直线l在平面α外的条件为________．(填序号)‎ 答案：①③‎ 解析：直线l在平面α外：l∥α或直线l与平面α仅有一个交点．‎ ‎2. (必修2P35练习7改编)在梯形ABCD中，AB∥CD，AB⊂平面α，CD⊄平面α，则直线CD与平面α内的直线的位置关系是________．‎ 答案：平行或异面 解析：因为AB∥CD，AB⊂平面α，CD⊄平面α，所以CD∥平面α，所以CD与平面α内的直线可能平行，也可能异面．‎ ‎3. (必修2P35练习4改编)在正六棱柱ABCDEFA1B‎1C1D1E‎1F1的表面中，与A‎1F1平行的平面是________．‎ 答案：平面ABCDEF、平面CC1D1D 解析：在正六棱柱中，易知A‎1F1∥AF，AF⊂平面ABCDEF，且A‎1F1⊄平面ABCDEF，所以A‎1F1∥平面ABCDEF.同理，A‎1F1∥C1D1，C1D1⊂平面CC1D1D，且A‎1F1⊄平面CC1D1D，所以A‎1F1∥平面CC1D1D.其他各面与A‎1F1均不满足直线与平面平行的条件．故答案为平面ABCDEF与平面CC1D1D.‎ ‎4. 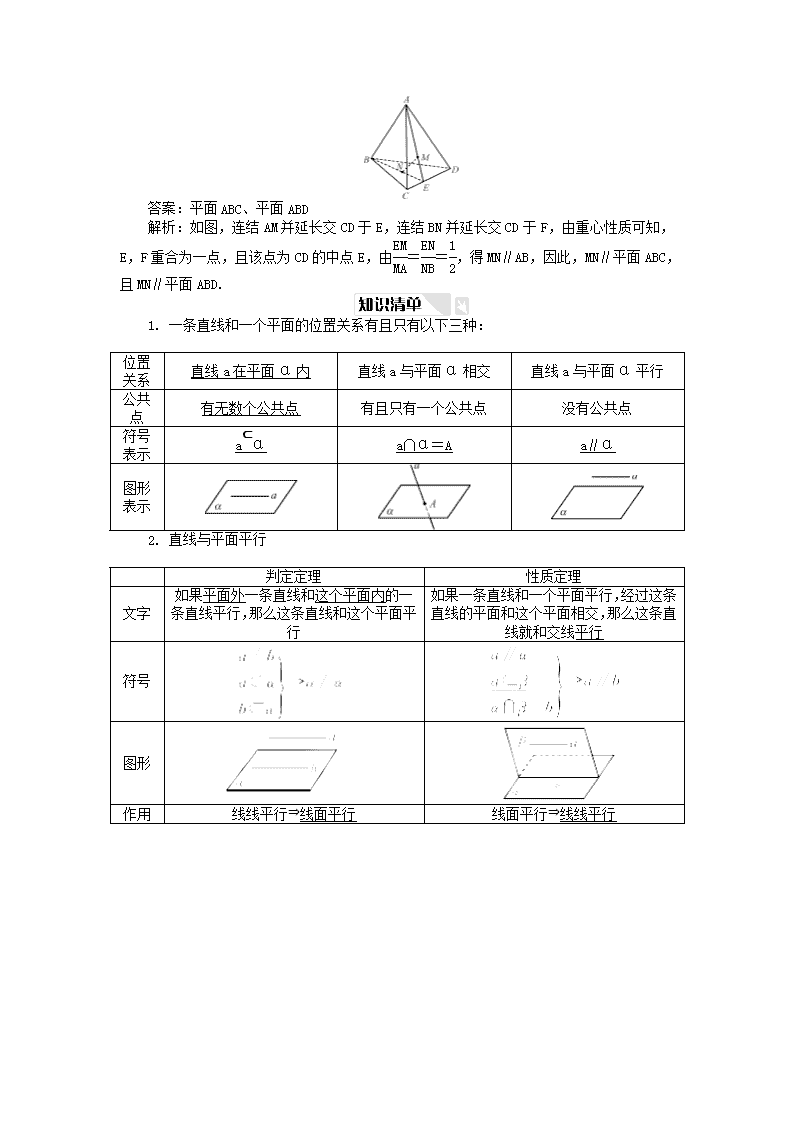(原创)P为矩形ABCD所在平面外一点，矩形对角线的交点为O，M为PB的中点，给出下列四个命题：‎ ‎① OM∥平面PCD；② OM∥平面PBC；③ OM∥平面PDA；④ OM∥平面PBA.‎ 其中正确命题的个数是________．‎ 答案：2‎ 解析：由已知OM∥PD，得OM∥平面PCD且OM∥平面PAD.故正确的只有①③.‎ ‎5. (必修2P41习题5改编)在四面体ABCD中，点M，N分别是△ACD，△BCD的重心，则四面体的四个面中与MN平行的是________．‎ 答案：平面ABC、平面ABD 解析：如图，连结AM并延长交CD于E，连结BN并延长交CD于F，由重心性质可知，E，F重合为一点，且该点为CD的中点E，由＝＝，得MN∥AB，因此，MN∥平面ABC，且MN∥平面ABD.‎ ‎1. 一条直线和一个平面的位置关系有且只有以下三种：‎ 位置关系 直线a在平面α内 直线a与平面α相交 直线a与平面α平行 公共点 有无数个公共点 有且只有一个公共点 没有公共点 符号表示 a⊂α a∩α＝A a∥α 图形表示 ‎2. 直线与平面平行 判定定理 性质定理 文字 如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行 如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行 符号 图形 作用 线线平行⇒线面平行 线面平行⇒线线平行 ‎
‎ ‎
‎ ‎
,　　　　　　　　　1　基本概念辨析)‎ ‎
,　　　　　1)　下列命题中真命题的个数为　　　　Ｗ.‎ ‎① 直线l平行于平面α内的无数条直线，则l∥α；‎ ‎② 若直线a在平面α外，则a∥α；‎ ‎③ 若直线a∥b，直线b⊂α，则a∥α；‎ ‎④ 若直线a∥b，b⊂α，那么直线a平行于平面α内的无数条直线.‎ 答案：1‎ 解析：∵ 直线l虽与平面α内无数条直线平行，但l有可能在平面α内，∴ l不一定平行于α.∴ ①是假命题.∵ 直线a在平面α外，包括两种情况：a∥α和a与α相交，∴ a和α不一定平行.∴ ②是假命题.∵ 直线a∥b，b⊂α，则只能说明a和b无公共点，但a可能在平面α内，∴ a不一定平行于α.∴ ③是假命题.∵ a∥b，b⊂α，那么a⊂α或a∥α，∴ a可以与平面α内的无数条直线平行.∴ ④是真命题.综上可知，真命题的个数为1.‎ 下列命题中正确的是　　　　Ｗ.（填序号）‎ ‎① 若直线a不在平面α内，则a∥α；‎ ‎② 若直线l上有无数个点不在平面α内，则l∥α；‎ ‎③ 若直线l与平面α平行，则l与α内的任意一条直线都平行；‎ ‎④ 若l与平面α平行，则l与α内任何一条直线都没有公共点；‎ ‎⑤ 平行于同一平面的两直线可以相交.‎ 答案：④⑤‎ 解析：如图①，a∩α＝A时，a⊄α，∴ ①错误；直线l与α相交时，l上有无数个点不在α内，∴ ②错误；l∥α时，α内的直线与l平行或异面，∴ ③错误；l∥α，l与α无公共点，∴ l与α内任一直线都无公共点，④正确；如图②，长方体ABCDA1B‎1C1D1中，A‎1C1与B1D1都与平面ABCD平行，∴ ⑤正确.‎ ‎
‎ ‎
,　　　　　　　　　2　线面平行的判定)‎ ‎
,　　　　　2)　如图，在底面为平行四边形的四棱锥PABCD中，点E是PC的中点.求证：PA∥平面BDE.‎ ‎
‎ 证明：如图，连结AC交BD于点O，连结OE.‎ ‎
‎ 在平行四边形ABCD中，O是AC的中点，又E是PC的中点，‎ ‎∴ OE∥PA.‎ ‎∵ PA⊄平面BDE，OE⊂平面BDE，‎ ‎∴ PA∥平面BDE.‎ ‎
变式训练 如图，在三棱柱A1B‎1C1ABC中， E，F分别是A1B，AC1的中点.求证：EF∥平面ABC.‎ ‎
‎ 证明：如图，连结A‎1C，因为三棱柱A1B‎1C1ABC中，四边形AA‎1C1C是平行四边形，所以点F在A‎1C上，且为A‎1C的中点.‎ 在△A1BC中，因为E，F分别是A1B，A‎1C的中点，‎ 所以EF∥BC.‎ 因为BC⊂平面ABC，EF⊄平面ABC，‎ 所以EF∥平面ABC.‎ ‎
‎ 如图，在正方体ABCDA1B‎1C1D1中，点M，N，P分别为棱AB，BC，C1D1的中点.求证：AP∥平面C1MN.‎ ‎
‎ 证明：在正方体ABCDA1B‎1C1D1中，‎ 因为点M，P分别为棱AB，C1D1的中点，所以AM＝PC1.‎ 又AM∥CD，PC1∥CD，故AM∥PC1，‎ 所以四边形AMC1P为平行四边形.从而AP∥C‎1M.‎ 又AP⊄ 平面C1MN，C‎1M⊂平面C1MN，‎ 所以AP∥平面C1MN.‎ ‎
,　　　　　　　　　3　线面平行的性质)‎ ‎
,　　　　　3)　如图，在直三棱柱ABCA1B‎1C1中，AC⊥BC，CC1＝4，M是棱CC1上的一点.若点N是AB的中点，且CN∥平面AB‎1M，求CM的长.‎ ‎
‎ 解：（解法1）如图①，取AB1的中点P，连结NP，PM.‎ ‎
①‎ 因为点N是AB的中点，所以NP∥BB1.‎ 因为CM∥BB1，所以NP∥CM，所以NP与CM共面.‎ 因为CN∥平面AB‎1M，平面CNPM∩平面AB‎1M＝MP，所以CN∥MP.‎ 所以四边形CNPM为平行四边形，所以CM＝NP＝CC1＝2.‎ ‎ （解法2）如图②，设NC与CC1确定的平面交AB1于点P，连结NP，PM.‎ ‎
②‎ 因为CN∥平面AB‎1M，CN⊂平面CNPM，平面AB‎1M∩平面CNPM＝PM，所以CN∥MP.‎ 因为BB1∥CM，BB1⊄平面CNPM，CM⊂平面CNPM，所以BB1∥平面CNPM.‎ 又BB1⊂平面ABB1，平面ABB1∩平面CNPM＝NP，‎ 所以BB1∥NP，所以CM∥NP，所以四边形CNPM为平行四边形.‎ 因为点N是AB的中点，所以CM＝NP＝BB1＝CC1＝2.‎ ‎（解法3）如图③，取BB1的中点Q，连结NQ，CQ.‎ ‎
③‎ 因为点N是AB的中点，所以NQ∥AB1.‎ 因为NQ⊄平面AB‎1M，AB1⊂平面AB‎1M，‎ 所以NQ∥平面AB‎1M.‎ 因为CN∥平面AB‎1M，NQ∩NC＝N，NQ，NC⊂平面NQC，‎ 所以平面NQC∥平面AB‎1M.‎ 因为平面BCC1B1∩平面NQC＝QC，平面BCC1B1∩平面AB‎1M＝MB1，所以CQ∥MB1.‎ 因为BB1∥CC1，所以四边形CQB‎1M是平行四边形，‎ 所以CM＝B1Q＝CC1＝2.‎ ‎（解法4）如图④，分别延长BC，B‎1M，设交点为S，连结AS.‎ ‎
④‎ 因为CN∥平面AB‎1M，CN⊂平面ABS，‎ 平面ABS∩平面AB‎1M＝AS，所以CN∥AS.‎ 由于AN＝NB，所以BC＝CS.‎ 又CM∥BB1，同理可得SM＝MB1，‎ 所以CM＝BB1＝CC1＝2.‎ 如图，在斜三棱柱ABCA1B‎1C1中，AC1与A‎1C交于点O，E是棱AB上一点，且OE∥平面BCC1B1.求证：点E是AB的中点.‎ ‎
‎ 证明：连结BC1，因为OE∥平面BCC1B1，‎ OE⊂平面ABC1，平面BCC1B1∩平面ABC1＝BC1，所以OE∥BC1.‎ 在斜三棱柱ABCA1B‎1C1中，侧面AA‎1C1C是平行四边形，AC1∩A‎1C＝O，‎ 所以点O是AC1的中点，‎ 所以＝＝1，即点E是AB的中点.‎ ‎
‎ ‎1. 如图，在直三棱柱ABCA1B‎1C1中，已知AB＝AC，点M，N，P分别为BC，CC1，BB1的中点.求证：A1N∥平面AMP.‎ ‎
‎ 证明：取C1B1的中点D，连结A1D，DN，DM，B‎1C.由于点D，M分别为C1B1，CB的中点，所以DM∥CC1且DM＝CC1，故DM∥AA1且DM＝AA1，则四边形A1AMD为平行四边形，所以A1D∥AM.又A1D⊄平面APM，AM⊂平面APM，所以A1D∥平面APM.由于D，N分别为C1B1，CC1的中点，所以DN∥B‎1C.‎ 又点P，M分别为BB1，CB的中点，所以MP∥B‎1C.‎ ‎
‎ 所以DN∥MP.‎ 又DN⊄平面APM，MP⊂平面APM，‎ 所以DN∥平面APM.‎ 由于A1D∩DN＝D，所以平面A1DN∥平面APM.‎ 由于A1N⊂平面A1DN，所以A1N∥平面APM.‎ ‎2. 如图，在四棱锥EABCD中，四边形ABCD为矩形，点M，N分别是AE，CD的中点.求证：直线MN∥平面EBC.‎ ‎
‎ 证明：取BE中点F，连结CF，MF.‎ 因为点M是AE的中点，所以MF綊AB.‎ 又点N是矩形ABCD边CD的中点，所以NC綊AB，所以MF綊NC，‎ 所以四边形MNCF是平行四边形，所以MN∥CF.‎ 又MN⊄平面EBC，CF⊂平面EBC，所以MN∥平面EBC.‎ ‎3. 如图，在正三棱柱ABCA′B′C′中，D是AA′上的点，点E是B′C′的中点，且A′E∥平面DBC′.试判断D点在AA′上的位置，并给出证明.‎ ‎
‎ 解：点D为AA′的中点.‎ 证明如下：如图，取BC的中点F，连结AF，EF，‎ ‎
‎ 设EF与BC′交于点O，连结DO，BE，C′F，‎ 在正三棱柱ABCA′B′C′中，点E是B′C′的中点，所以 EF∥BB′∥AA′，且EF＝BB′＝AA′，‎ 所以四边形A′EFA是平行四边形.‎ 因为A′E∥平面DBC′，A′E⊂平面A′EFA，且平面DBC′∩平面A′EFA＝DO，‎ 所以A′E∥DO.‎ 在正三棱柱ABC－A′B′C′中，点E是B′C′的中点，‎ 所以EC′∥BC且EC′＝BF，所以四边形BFC′E是平行四边形，所以点O是EF的中点.‎ 因为在平行四边形A′EFA中， A′E∥DO，‎ 所以点D为AA′的中点.‎ ‎4. 如图，在直四棱柱ABCDA1B‎1C1D1中，底面ABCD是菱形，点E是A‎1C1的中点.求证：BE∥平面ACD1.‎ ‎
‎ 证明：如图，连结B1D1交A‎1C1于点E，连结BD交AC于点O，连结OD1.‎ ‎∵ 在直四棱柱ABCDA1B‎1C1D1中，底面ABCD是菱形，‎ ‎∴ D1E∥BO且D1E＝BO，‎ ‎∴ 四边形BED1O是平行四边形，‎ ‎∴ BE∥OD1.‎ ‎∵ OD1⊂平面ACD1，BE⊄平面ACD1，‎ ‎∴ BE∥平面ACD1.‎ ‎
‎ ‎5. 如图，在四棱锥PABCD中，PC⊥平面PAD，AB∥CD，CD＝2AB＝2BC，点M，N分别是棱PA，CD的中点.求证：PC∥平面BMN.‎ ‎
‎ 证明：设AC∩BN＝O，连结MO，AN.‎ 因为AB＝CD，AB∥CD，点N为CD的中点，‎ 所以AB＝CN，AB∥CN，‎ 所以四边形ABCN为平行四边形，‎ 所以O为AC的中点.‎ 又点M为PA的中点，所以MO∥PC.‎ 因为MO⊂平面BMN，PC⊄ 平面BMN，‎ 所以PC∥平面BMN.‎ ‎
‎ ‎
‎ ‎1. 如图，在三棱锥PABC中，点M，N分别为AB，PA的中点.求证：PB∥平面MNC.‎ 证明：因为点M，N分别为AB，PA的中点，‎ 所以MN∥PB.‎ 因为MN⊂平面MNC，PB⊄ 平面MNC，‎ 所以PB∥平面MNC.‎ ‎2. 如图，在直三棱柱ABCA1B‎1C1中，点D是AB的中点.求证：BC1∥ 平面A1CD.‎ ‎
‎ 证明：连结AC1，设交A‎1C于点O，连结OD.‎ ‎∵ 四边形AA‎1C1C是矩形，∴ O是AC1的中点.‎ ‎∵ 在△ABC1中， O，D分别是AC1，AB的中点，‎ ‎∴ OD∥BC1.‎ ‎∵ OD⊂平面A1CD，BC1⊄平面A1CD，‎ ‎∴ BC1∥平面A1CD.‎ ‎3. 如图，在长方体ABCDA1B‎1C1D1中，点P∈BB1（P不与B，B1重合）.PA∩A1B＝M，PC∩BC1＝N.‎ 求证：MN∥平面ABCD.‎ ‎
‎ 证明：连结AC，A‎1C1，‎ 在长方体ABCDA1B‎1C1D1中，‎ AA1∥CC1，且AA1＝CC1，‎ ‎
‎ ‎∴ 四边形ACC‎1A1是平行四边形.‎ ‎∴ AC∥A‎1C1.‎ ‎∵ AC⊄平面A1BC1，A‎1C1⊂‎ 平面A1BC1，‎ ‎∴ AC∥平面A1BC1.‎ ‎∵ AC⊂平面PAC，平面A1BC1∩‎ 平面PAC＝MN，‎ ‎∴ AC∥MN.‎ ‎∵ MN⊄平面ABCD，‎ AC⊂平面ABCD，‎ ‎∴ MN∥平面ABCD.‎ ‎
‎ ‎1. 判定或证明直线与平面平行的常用方法 ‎（1） 利用直线与平面平行的定义（无公共点）.‎ ‎（2） 利用直线与平面平行的判定定理（a⊄α，b⊂α，a∥b⇒a∥α）.‎ ‎（3） 利用平面与平面平行的性质（α∥β，a⊂α⇒a∥β）.‎ 注意不管用哪种方法，都应将相应的条件写全，缺一不可.‎ ‎2. 直线与平面平行的性质定理的作用是证线线平行，应用时常常需构造辅助平面，和在平面几何中添加辅助线一样，在构造辅助平面时要确认这个平面的存在性.‎ ‎3. 证明平行问题时要注意“转化思想”的应用，要抓住线线、线面、面面之间的平行关系，实现“空间问题”与“平面问题”之间的转化.‎ ‎[备课札记]‎