高中数学选修1-2课件：3_《 直接证明》 14页

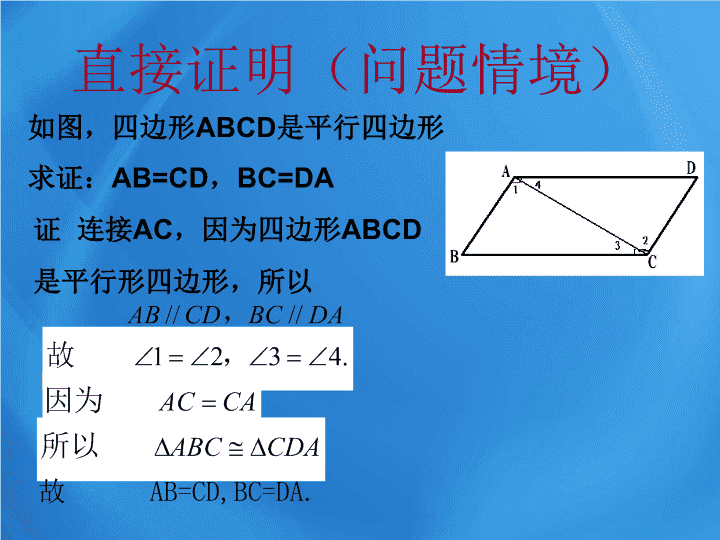
2.2 直接证明 ( 一 ) 分析法 综合法 直接证明（问题情境） 如图，四边形 ABCD 是平行四边形 求证： AB=CD ， BC=DA 证 连接 AC ，因为四边形 ABCD 是平行形四边形，所以 故 AB=CD,BC=DA. 直接证明 1 概念 直接从原命题的条件逐步推得命题成立 2 直接证明的一般形式： 直接证明（学生活动） 证法 1 对于正数 a,b, 有 直接证明 证法 2 要证 只要证 只要证 只要证 因为最后一个不等式成立，故结论成立。 直接证明（数学理论） 上述两种证法有什么异同？ 都是直接证明 证法 1 从已知条件出发，以已知的定义、公理、定理为依据，逐步下推，直到推出要证明的结论为止 综合法 相同 不同 证法 2 从问题的结论出发，追溯导致结论成立的条件，逐步上溯，直到使结论成立的条件和已知条件吻合为止 分析法 直接证明 综合法和分析法的推证过程如下： 综合法 已知条件 结论 分析法 结论 已知条件 直接证明（例题） 直接证明 证 （ 综合法 ） 因为 因为 所以 又因为 所以 所以 所以 直接证明 证 （ 分析法 ）要证明 CE=DF ，只需证明 为此只需证明 为了证明 只需 为了证明 只需证明 也只需 因为 是对顶角，所以它们相等，从而 成立，因此命题成立 . 分析法 解题方向比较明确， 利于寻找解题思路； 综合法 条理清晰，易于表述。 通常以 分析法 寻求 思路，再用 综合法 有条理地 表述解题过程 直接证明（练习） 直接证明（练习） 证 要证 只需证明 只需证明 只需证明 所以原命题成立 . 直接证明 3.△ABC 三边长 的倒数成等差数列，求证： . 证明： 因为 a,b,c 为 △ ABC 三边 所以 a + c > b 所以 cosB>0 因此 直接证明（回顾小结） 分析法 解题方向比较明确， 利于寻找解题思路； 综合法 条理清晰，易于表述。 通常以 分析法 寻求 思路，再用 综合法 有条理地 表述解题过程 分析法 综合法 概念