高考数学复习单元评估检测(二) 15页

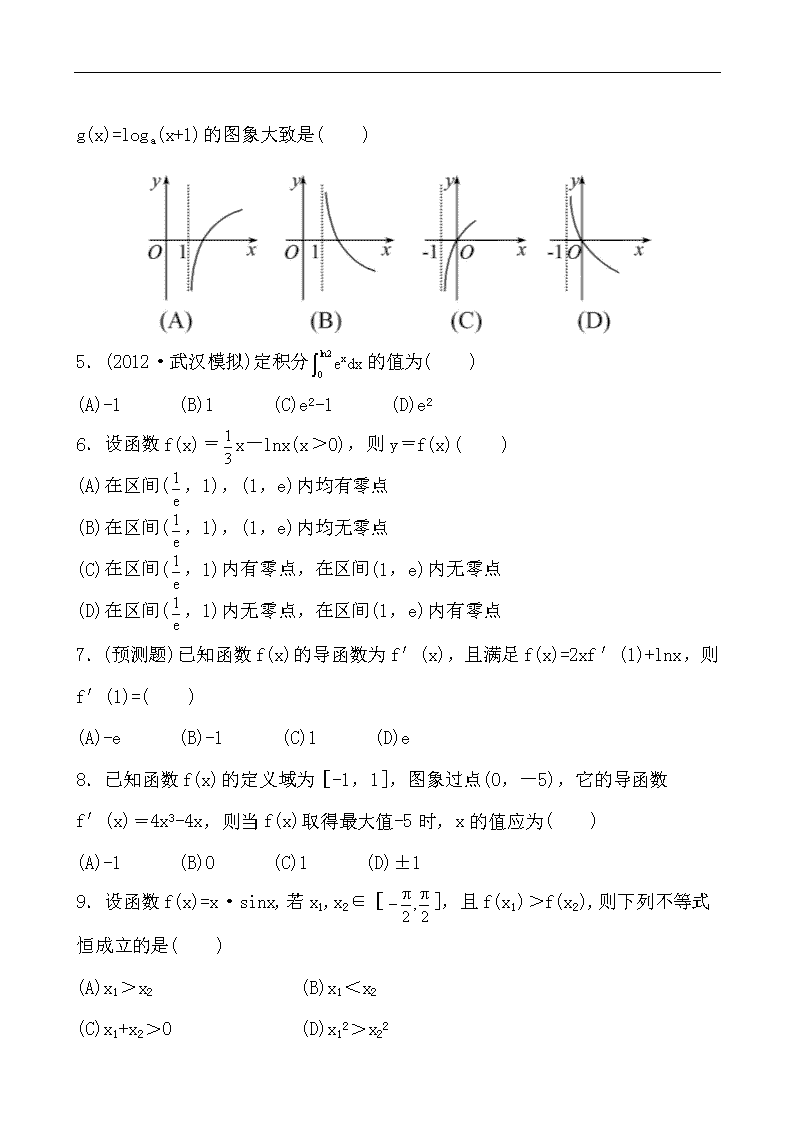
‎ ‎ 单元评估检测(二)‎ ‎(第二章)‎ ‎(120分钟　150分)‎ 一、选择题(本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1.下列图形中可以表示以M={x|0≤x≤1}为定义域，以N={y|0≤y≤1}为值域的函数的图象是( )‎ ‎2.函数f(x)对任意x∈R,恒有f(x+2)=-f(x)，且f(1)=2,则f(11)=( )‎ ‎(A)-2　　　(B)2　　　(C)0　　　(D)1‎ ‎3.(2011·广东高考)设函数f(x)和g(x)分别是R上的偶函数和奇函数，则下列结论恒成立的是( )‎ ‎(A)f(x)+|g(x)|是偶函数 ‎(B)f(x)-|g(x)|是奇函数 ‎(C)|f(x)|+g(x)是偶函数 ‎(D)|f(x)|-g(x)是奇函数 ‎4．已知函数f(x)=ax(a>0,a≠‎ ‎1)是定义在R上的单调递减函数，则函数g(x)=loga(x+1)的图象大致是( )‎ ‎5．(2012·武汉模拟)定积分的值为( )‎ ‎(A)-1　　　(B)1　　　(C)e2-1　　　(D)e2‎ ‎6．设函数f(x)＝x－lnx(x＞0)，则y＝f(x)( )‎ ‎(A)在区间(，1)，(1，e)内均有零点 ‎(B)在区间(，1)，(1，e)内均无零点 ‎(C)在区间(，1)内有零点，在区间(1，e)内无零点 ‎(D)在区间(，1)内无零点，在区间(1，e)内有零点 ‎7．(预测题)已知函数f(x)的导函数为f′(x)，且满足f(x)=2xf′(1)+lnx，则 f′(1)=( )‎ ‎(A)-e　　　(B)-1　　　(C)1　　　(D)e ‎8．已知函数f(x)的定义域为［-1，1］，图象过点(0，－5)，它的导函数 f′(x)＝4x3-4x，则当f(x)取得最大值-5时，x的值应为( )‎ ‎(A)-1　　　(B)0　　　(C)1　　　(D)±1‎ ‎9．设函数f(x)=x·sinx,若x1,x2∈［］，且f(x1)＞f(x2),则下列不等式恒成立的是( )‎ ‎(A)x1＞x2 (B)x1＜x2‎ ‎(C)x1+x2＞0 (D)x12＞x22‎ ‎10．(2011·湖南高考)已知函数f(x)=ex-1,g(x)=-x2+4x-3.若有f(a)=g(b)，则b的取值范围为( )‎ ‎(A)[2-,2+] (B)(2-,2+)‎ ‎(C)[1,3] (D)(1,3)‎ 二、填空题(本大题共5小题，每小题4分，共20分.请把正确答案填在题中横线上)‎ ‎11．计算(lg-lg25)÷=______.‎ ‎12．已知直线y=x+1与曲线y=ln(x+a)相切，则a的值为______．‎ ‎13.（2012·南平模拟）函数f(x)=2x3-3x2+10的单调递减区间为______.‎ ‎14．函数f(x)=(x+a)3对任意t∈R，总有f(1+t)=-f(1-t)，则f(2)+f(-2)等于______.‎ ‎15．(2011·四川高考)函数f(x)的定义域为A，若x1,x2∈A且f(x1)=f(x2)时总有x1=x2，则称f(x)为单函数.例如，函数f(x)=2x+1(x∈R)是单函数.下列命题：‎ ‎①函数f(x)=x2(x∈R)是单函数；‎ ‎②若f(x)为单函数，x1,x2∈A且x1≠x2，则f(x1)≠f(x2)；‎ ‎③若f:A→B为单函数，则对于任意b∈B,A中至多有一个元素与之对应；‎ ‎④函数f(x)在某区间上具有单调性，则f(x)一定是单函数.‎ 其中的真命题是______.(写出所有真命题的编号)‎ 三、解答题(本大题共6小题，共80分.解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎16．(13分)求下列关于x的函数的定义域和值域：‎ ‎(1) ‎ ‎(2)y=log2(-x2+2x);‎ ‎(3)‎ x ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ y ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎17．(13分)（易错题）两个二次函数f(x)=x2+bx+c与g(x)=-x2+2x+d的图象有唯一的公共点P(1,-2)．‎ ‎(1)求b,c,d的值；‎ ‎(2)设F(x)=(f(x)+m)·g′(x)，若F(x)在R上是单调函数，求m的取值范围，并指出F(x)是单调递增函数，还是单调递减函数．‎ ‎18．(13分)(2011·北京高考)已知函数 ‎(1)求f(x)的单调区间；‎ ‎(2)若对于任意的x∈(0，+∞)，都有求k的取值范围．‎ ‎19．(13分)某市旅游部门开发一种旅游纪念品，每件产品的成本是15元，销售价是20元，月平均销售a件.通过改进工艺，产品的成本不变，质量和技术含金量提高，市场分析的结果表明，如果产品的销售价提高的百分率为x(00)．‎ ‎(1)求g(x)的表达式；‎ ‎(2)若存在x∈(0，+∞)，使f(x)≤0成立，求实数m的取值范围；‎ ‎(3)设10的图象，可知g(x)与h(x)的图象在(,1)内无交点，在(1,e)内有1个交点，故选D.‎ ‎【变式备选】已知函数则关于x的方程f(x)=log2‎ x解的个数为( )‎ ‎(A)4　　　(B)3　　　(C)2　　　(D)1‎ ‎【解析】选B.在同一直角坐标系中画出y=f(x)与y=log2x的图象，从图象中可以看出两函数图象有3个交点，故其解有3个.‎ ‎7．【解析】选B.f′(x)=‎2f′(1)+，令x=1得f′(1)=‎2f′(1)+1，∴f′(1)=-1，故选B．‎ ‎8．【解析】选B.易知f(x)=x4-2x2-5,f′(x)=0时x=0或x=±1,又因为定义域为［-1，1］，只有f(0)=-5,所以x=0.‎ ‎9．【解析】选D.显然f(x)为偶函数，‎ 当x∈(0, ］时,f′(x)=sinx+xcosx＞0，‎ ‎∴f(x)在(0, ］上单调递增.‎ 又f(x1)＞f(x2)⇔f(|x1|)＞f(|x2|)⇔|x1|＞|x2|⇔x12＞x22．‎ ‎10．【解析】选B.∵f(a)>-1,∴g(b)>-1,‎ ‎∴-b2+4b-3>-1,∴b2-4b+2<0,‎ ‎∴2-0,∴00；0，f(x)在区间(64，640)上为增函数，‎ 所以f(x)在x=64处取得最小值，此时，‎ 故需新建9个桥墩才能使y最小．‎ ‎20.【解析】（1）f(x+y)=f(x)+f(y)(x,y∈R), ①‎ 令x=y=0,代入①式，得f(0+0)=f(0)+f(0),即f(0)=0.‎ 令y=-x,代入①式，得f(x-x)=f(x)+f(-x),又f(0)=0,则有0＝f(x)+f(-x).‎ 即f(-x)=-f(x)对任意x∈R成立，所以f(x)是奇函数.‎ ‎（2）f(3)=log23>0,即f(3)>f(0),又f(x)在R上是单调函数，所以f(x)在R上是增函数，又由(1)知f(x)是奇函数.所以有f(k·3x)<-f(3x-9x-2)=f(-3x+9x+2),‎ 即k·3x<-3x+9x+2,‎ ‎32x-(1+k)·3x+2>0对任意x∈R成立.‎ 令t=3x>0,问题等价于t2-(1+k)t+2>0对任意t>0恒成立.‎ 令g(t)=t2-(1+k)t+2,其对称轴.‎ 当<0即k<-1时，g(0)=2>0,符合题意；‎ 当=0即k=-1时，g(t)=t2+2,‎ 对任意t>0,g(t)>0恒成立；‎ 当>0时，对任意t>0，g(t)>0恒成立,‎ 解得-10).‎ 当m>0时，由对数函数的性质知，f(x)的值域为R；‎ 当m=0时，f(x)=，对任意x>0，f(x)>0恒成立；‎ 当m<0时，由f′(x)=x+=0得 列表：‎ x ‎(0, )‎ ‎(,+∞)‎ f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ ‎↘‎ 极小值 ‎↗‎ 这时f(x)min=f()=‎ 由f(x)min≤0得所以m≤-e,‎ 综上，存在x>0使f(x)≤0成立，实数m的取值范围是(-∞,-e］∪(0,+∞)．‎ ‎(3)由题知H(x)=x2-(m+1)x+mlnx, 因为对任意x∈［1,m］，所以H(x)在［1,m］内单调递减.‎ 于是|H(x1)-H(x2)|≤H(1)-H(m)=m2-mlnm-.‎ 要使|H(x1)-H(x2)|<1恒成立，则需m2-mlnm-<1成立，‎ 即m-lnm-<0.‎ 记则 所以函数h(m)=m-lnm-在(1,e］上是单调增函数，‎ 所以h(m)≤h(e)=-1-=<0，故命题成立.‎