山东省潍坊市五县市2019-2020学年高二下学期期中考试数学试题 13页

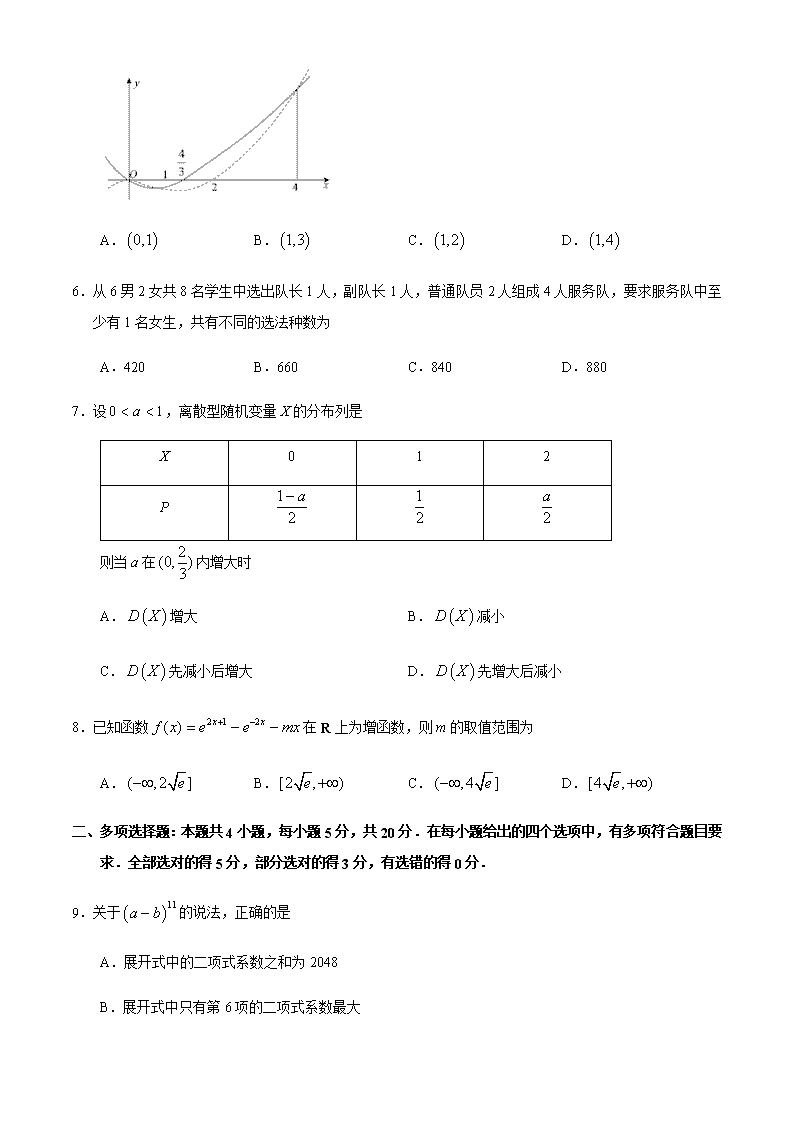
保密★启用前 ‎2019—2020学年度第二学期监测 高二数学 ‎2020.5‎ 本试卷共4页，共150分，考试时间120分钟．‎ 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设函数，则 A．0 B．1 C．2 D．‎ ‎2．若，则 A．6 B．7 C．8 D．9‎ ‎3．一物体做直线运动，其位移s（单位：m）与时间t（单位：s）的关系是，则该物体在时的瞬时速度为 A．3 B．7 C．6 D．1‎ ‎4．函数有 A．极大值6，极小值2 B．极大值2，极小值6‎ C．极小值，极大值2 D．极小值2，极大值8‎ ‎5．已知函数与的图象如图所示，则不等式组解集为 A． B． C． D．‎ ‎6．从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有不同的选法种数为 A．420 B．660 C．840 D．880‎ ‎7．设，离散型随机变量X的分布列是 X ‎0‎ ‎1‎ ‎2‎ P 则当a在内增大时 A．增大 B．减小 C．先减小后增大 D．先增大后减小 ‎8．已知函数在R上为增函数，则m的取值范围为 A． B． C． D．‎ 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分．‎ ‎9．关于的说法，正确的是 A．展开式中的二项式系数之和为2048‎ B．展开式中只有第6项的二项式系数最大 C．展开式中第6项和第7项的二项式系数最大 D．展开式中第6项的系数最大 ‎10．已知函数，则 A．函数一定存在最值 B．，‎ C．若是的极值点，则 D．若是的极小值点，则在区间单调递增 ‎11．甲、乙两类水果的质量（单位：kg）分别服从正态分布，，其正态分布的密度曲线如图所示，则下列说法正确的是 A．乙类水果的平均质量 B．甲类水果的质量比乙类水果的质量更集中于平均值左右 C．甲类水果的平均质量比乙类水果的平均质量小 D．乙类水果的质量服从的正态分布的参数 ‎12．已知函数，则以下结论正确的是 A．函数的单调减区间是（0，2）‎ B．函数有且只有1个零点 C．存在正实数k，使得成立 D．对任意两个正实数，，且，若，则 三、填空题：本题共4小题，每小题5分，共20分．‎ ‎13．曲线在点处的切线方程为______．‎ ‎14．用1，2，3，4，5这5个数字组成的没有重复数字的四位数中，能被5整除的数的个数为______（用数字作答）‎ ‎15．盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色相同外完全相同．从盒中一次随机取出4个球，设X表示取出的三种颜色球的个数的最大数，则______．‎ ‎16．设函数，若不等式对一切恒成立，则______，的取值范围为____．（第一空2分，第二空3分）‎ 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（10分）求下列函数的导数：‎ ‎（1）；‎ ‎（2）．‎ ‎18．（12分）‎ ‎2020年寒假是特殊的寒假，因为抗击疫情全体学生只能在家进行网上在线学习，为了研究学生在网上学习的情况，某学校在网上随机抽取120名学生对线上教育进行调查，其中男生与女生的人数之比为11:13，其中男生30人对于线上教育满意，女生中有15名表示对线上教育不满意．‎ ‎（1）完成列联表，并回答能否有99%的把握认为对“线上教育是否满意与性别有关”；‎ 满意 不满意 总计 男生 ‎20‎ 女生 ‎15‎ 合计 ‎120‎ ‎（2）从被调查的对线上教育满意的学生中，利用分层抽样抽取8名学生，再在8名学生中抽取3名学生，作线上学习的经验介绍，其中抽取男生的个数为，求出的分布列及期望值．‎ 参考公式：附：‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.072‎ ‎0.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10828‎ ‎19．（12分）‎ 已知函数．‎ ‎（1）当时，求函数的单调区间；‎ ‎（2）若函数在处取得极大值，求实数的取值范围．‎ ‎20．（12分）‎ 某工厂生产某种型号的农机具零配件，为了预测今年7月份该型号农机具零配件的市场需求量，以合理安排生产，工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查，销售单价x（单位：元）和销售量y（单位：千件）之间的6组数据如下表所示：‎ 月份 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 销售单价（元）‎ ‎11.1‎ ‎9.1‎ ‎9.4‎ ‎10.2‎ ‎8.8‎ ‎11.4‎ 销售量（千件）‎ ‎2.5‎ ‎3.1‎ ‎3‎ ‎2.8‎ ‎3.2‎ ‎2.4‎ ‎（1）根据1至6月份的数据，求y关于x的线性回归方程（系数精确到0.01）；‎ ‎（2）结合（1）‎ 中的线性回归方程，假设该型号农机具零配件的生产成本为每件3元，那么工厂如何制定7月份的销售单价，才能使该月利润达到最大？（计算结果精确到0.1）‎ 参考公式：回归直线方程，‎ 参考数据：．‎ ‎21．（12分）‎ 为保护环境，某市有三家工厂要建造污水处理厂．三家工厂分别位于矩形ABCD的顶点AB及CD的中点P处，已知，按照规划要求污水处理厂建在矩形ABCD的区域上（含边界），且与A，B等距离的一点O处，并铺设排污管道AO，BO，OP，设排污管道的总长为ykm．‎ ‎（1）按下列要求写出函数关系式：‎ ‎①设，将y表示成的函数关系式；‎ ‎②设，将y表示成x的函数关系式；‎ ‎（2）请你选用（1）中的一个函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短．‎ ‎22．（12分）‎ 已知函数．‎ ‎（1）当时，讨论函数的单调性；‎ ‎（2）若函数在区间上无零点，求的取值范围 高二数学试题参考答案 ‎2020.5‎ 一、单项选择题：本题共8小题，每小题5分，共40分．‎ ‎1-4BCDA 5-8BBDC 二、多项选择题：本题共4小题，每小题5分，共20分．‎ ‎9．AC 10．BC 11．ABC 12．ABD 三、填空题：本题共4小题，每小题5分，共20分．‎ ‎13． 14．24‎ ‎15． 16．3‎ 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．解：（1）‎ ‎．‎ ‎（2），‎ 则．‎ ‎18．解：（1）因为男生人数为：，‎ 所以女生人数为，‎ 于是可完成2×2列联表，如下：‎ 满意 不满意 总计 男生 ‎20‎ ‎25‎ ‎25‎ 女生 ‎50‎ ‎15‎ ‎65‎ 合计 ‎80‎ ‎40‎ ‎120‎ 根据列联表中的数据，得到的观测值 ‎，‎ 所以有99%的把握认为对“线上教育是否满意与性别有关”．‎ ‎（2）由（1）可知男生抽3人，女生抽5人，‎ 依题可知的可能取值为0，1，2，3，并且服从超几何分布，‎ ‎，即 ‎，‎ ‎，．‎ 可得分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 可得．‎ ‎19．解：（1）的定域为，‎ 当时，，‎ 令得，令得，‎ 所以的增区间为，减区间为.‎ ‎（2）‎ ‎①当时，若，则，‎ 此时，在单调递增，‎ 所以函数在处不可能取得极大值，不合题意．‎ ‎②当时，‎ ‎1‎ ‎0‎ ‎↗‎ 极大值 ‎↘‎ 函数在处取得极大值．‎ 综上可知，a的取值范围是．‎ ‎20．解：（1）由条件知，，，‎ ‎，‎ 从而，‎ 故关于x的线性回归方程为．‎ ‎（2）假设7月份的销售单价为x元，‎ 则由（1）可知，7月份零配件销量为，‎ 故7月份的利润，‎ 其对称轴，‎ 故7月份销售单价为11.3元时，该月利润才能达到最大．‎ ‎21．解：（1）①由条件知PQ垂直平分AB，若，‎ 则，故，‎ 又，‎ 所以，‎ 所求函数关系式为 ‎．‎ ‎②若，则，‎ 所 所求函数关系式为 ‎（2）选择函数模型①，‎ 令得，所以，‎ 当时，，y是的减函数；‎ 当时，，y是的增函数；‎ 所以当时，．‎ 这时点位于线段AB的中垂线上，且距离AB边处．‎ ‎（若选择②请自行解答）‎ ‎22．（12分）‎ 解：（1）当时，，定义域为，‎ 则，‎ 令，得，‎ 令，得，‎ ‎∴的单调递减区间为，单调递增区间为 ‎（2）∵函数在区间上无零点，‎ ‎∴在区间上，恒成立或恒成立 ‎，‎ ‎．‎ ‎①当时，，‎ 在区间，，‎ 记，‎ 则，‎ 在区间上，‎ ‎∴在区间上，单调递减，‎ ‎∴‎ 即，‎ ‎∴，‎ 即在区间上恒成立，满足题意；‎ ‎②当时，‎ ‎．‎ ‎∵，，‎ ‎∴，‎ ‎∴在上有零点，‎ 即函数在区间上有零点，不符合题意 综上所述，．‎