高考数学复习课时提能演练(十一) 2_8 9页

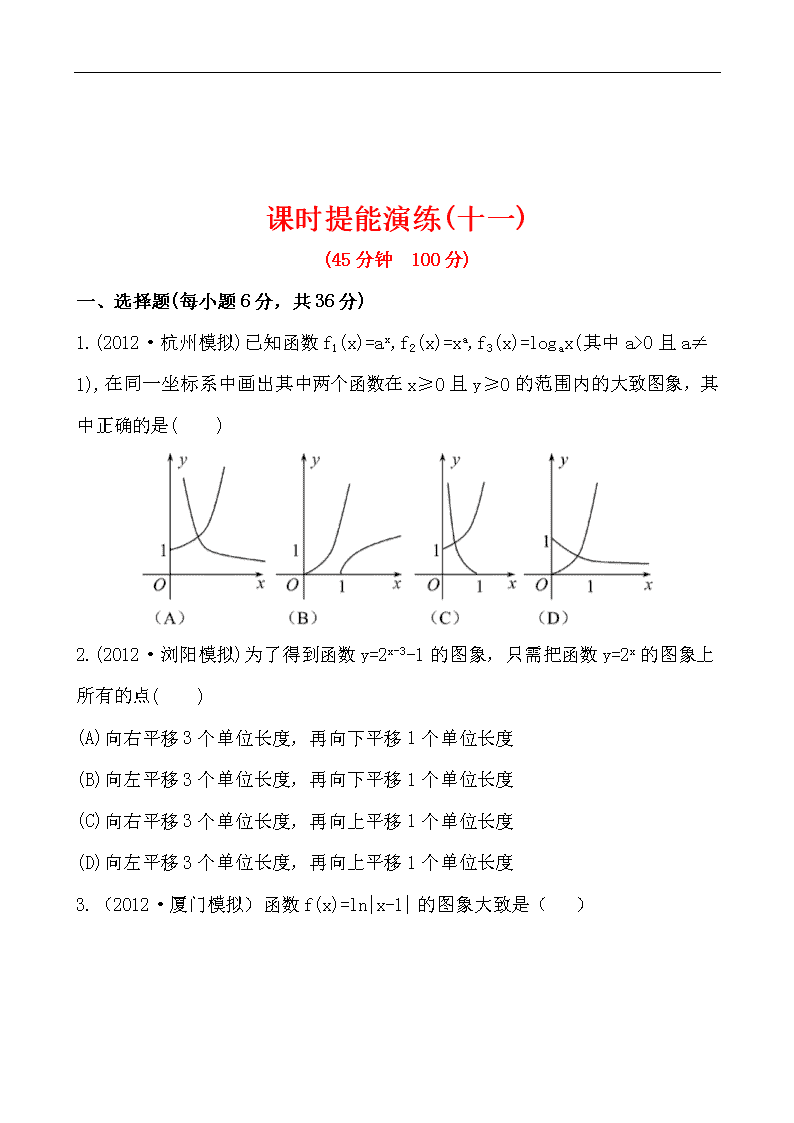
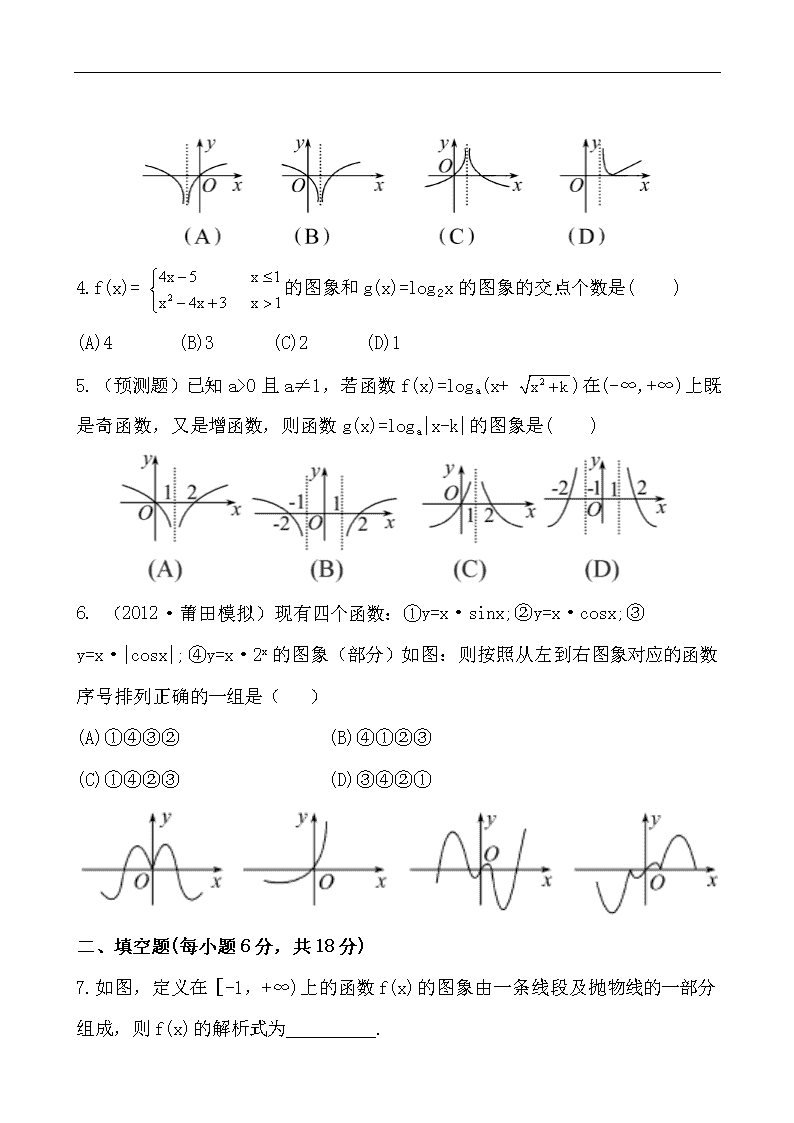
‎ ‎ 课时提能演练(十一)‎ ‎(45分钟 100分)‎ 一、选择题(每小题6分，共36分)‎ ‎1.(2012·杭州模拟)已知函数f1(x)=ax,f2(x)=xa,f3(x)=logax(其中a>0且a≠1),在同一坐标系中画出其中两个函数在x≥0且y≥0的范围内的大致图象，其中正确的是( )‎ ‎2.(2012·浏阳模拟)为了得到函数y=2x-3-1的图象，只需把函数y=2x的图象上所有的点( )‎ ‎(A)向右平移3个单位长度，再向下平移1个单位长度 ‎(B)向左平移3个单位长度，再向下平移1个单位长度 ‎(C)向右平移3个单位长度，再向上平移1个单位长度 ‎(D)向左平移3个单位长度，再向上平移1个单位长度 ‎3.（2012·厦门模拟）函数f(x)=ln|x-1|的图象大致是（ ）‎ ‎4.f(x)= 的图象和g(x)=log2x的图象的交点个数是( )‎ ‎(A)4 (B)3 (C)2 (D)1‎ ‎5.（预测题）已知a>0且a≠1，若函数f(x)=loga(x+ )在(-∞,+∞)上既是奇函数，又是增函数，则函数g(x)=loga|x-k|的图象是( )‎ ‎6. （2012·莆田模拟）现有四个函数：①y=x·sinx;②y=x·cosx;③y=x·|cosx|;④y=x·2x的图象（部分）如图：则按照从左到右图象对应的函数序号排列正确的一组是（ ）‎ ‎(A)①④③② (B)④①②③‎ ‎(C)①④②③ (D)③④②①‎ 二、填空题(每小题6分，共18分)‎ ‎7.如图，定义在［-1，+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成，则f(x)的解析式为__________.‎ ‎8.(2012·临沂模拟)若函数y=f(x)(x∈R)满足f(x+2)=f(x)，且x∈［-1,1)时，f(x)=|x|，则函数y=f(x)的图象与函数y=log4|x|的图象的交点的个数为___________.‎ ‎9.已知函数f(x)=()x的图象与函数y=g(x)的图象关于直线y=x对称，令h(x)=g(1-|x|)，则关于h(x)有下列命题：‎ ‎①h(x)的图象关于原点对称；‎ ‎②h(x)为偶函数；‎ ‎③h(x)的最小值为0；‎ ‎④h(x)在(0，1)上为减函数.‎ 其中正确命题的序号为_________.(将你认为正确的命题的序号都填上)‎ 三、解答题(每小题15分，共30分)‎ ‎10.作出下列函数的大致图象 ‎(1)y=x2-2|x|;‎ ‎(2)y= ［3(x+2)］;‎ ‎(3)y=.‎ ‎11．(易错题)(1)已知函数y=f(x)的定义域为R，且当x∈R时，f(m+x)=f(m-x)恒成立，求证y=f(x)的图象关于直线x=m对称；‎ ‎(2)若函数y=log2|ax-1|的图象的对称轴是x=2,求非零实数a的值.‎ ‎【探究创新】‎ ‎(16分)已知函数y=f(x)同时满足以下五个条件：‎ ‎(1)f(x+1)的定义域是［-3，1］；‎ ‎(2)f(x)是奇函数；‎ ‎(3)在［-2，0)上，f′(x)>0;‎ ‎(4)f(-1)=0;‎ ‎(5)f(x)既有最大值又有最小值.‎ 请画出函数y=f(x)的一个图象，并写出相应于这个图象的函数解析式.‎ 答案解析 ‎1.【解析】选B.结合图象逐个验证知，B正确.‎ ‎2.【解析】选A.把y=2x的图象向右平移3个单位长度得到y=2x-3的图象，再向下平移1个单位长度得到y=2x-3-1的图象，故选A.‎ ‎3.【解析】选B.f(x)=ln|x-1|=,图象关于x=1对称.‎ ‎4.【解析】选C.在同一坐标系中作出f(x)和g(x)的图象如图所示，‎ 由图象知有两个交点，故选C.‎ ‎【误区警示】本题易由于作图没有去掉(1，0)点，而误选B.‎ ‎5.【解题指南】由已知先求出k的值，并判断出a与1的大小关系，再由g(x)选图象.‎ ‎【解析】选A.由已知f(0)=0,得loga=0，∴k=1,‎ ‎∴f(x)=loga(x+ ),又∵其为增函数，‎ ‎∴a>1.故g(x)=loga|x-1|的图象可由y=loga|x|的图象向右平移一个单位得到，且在(-∞,1)上为减函数，在(1,+∞)上为增函数，故选A.‎ ‎6.【解析】选C.①y=x·sinx是偶函数；②y=x·cosx是奇函数；③y=x|cosx|是奇函数且当x>0时，f(x)≥0恒成立；④y=x·2x是非奇非偶函数.‎ ‎7.【解析】当x∈［-1,0］时，设y=kx+b,由图象得得，∴y=x+1,当x>0时，设y=a(x-2)2-1,由图象得：0=a(4-2)2-1得a= ,‎ ‎∴y= (x-2)2-1,‎ 综上可知 答案：‎ ‎8.【解析】∵函数y=f(x)满足f(x+2)=f(x)，‎ ‎∴该函数的周期为2，又∵x∈［-1,1)时，f(x)=|x|，‎ ‎∴可得到该函数的图象，在同一直角坐标系中，画出两函数的图象如图，可得交点有6个.‎ 答案:6‎ ‎9.【解题指南】先求g(x),再求h(x)并化简，最后判断.‎ ‎【解析】g(x)= x,‎ ‎∴h(x)= (1-|x|),‎ ‎∴h(x)= ‎ 得函数h(x)的大致图象如图，故正确命题序号为②③.‎ 答案：②③‎ ‎10.【解析】(1)y= 的图象如图(1).‎ ‎(2)y= 3+ (x+2)=-1+ (x+2)，其图象如图(2).‎ ‎(3)y=，其图象如图(3).‎ ‎11．【解析】(1)设P(x0,y0)是y=f(x)图象上任意一点，‎ 则y0=f(x0).又P点关于x=m的对称点为P′,则P′的坐标为 ‎(‎2m-x0,y0).由已知f(m+x)=f(m-x),得 f(‎2m-x0)=f(m+(m-x0))‎ ‎=f(m-(m-x0))=f(x0)=y0.即 P′(‎2m-x0,y0)在y=f(x)的图象上.‎ ‎∴y=f(x)的图象关于直线x=m对称.‎ ‎(2)由题意知对定义域内的任意x,有f(2-x)=f(2+x)恒成立.‎ ‎∴|a(2-x)-1|=|a(2+x)-1|恒成立，‎ 即|-ax+(‎2a-1)|=|ax+(‎2a-1)|恒成立.‎ 又∵a≠0,∴‎2a-1=0,得 a=.‎ ‎【方法技巧】函数对称问题解题技巧 ‎(1)证明函数图象的对称性，只需证明其图象上的任意一点关于对称中心(对称轴)的对称点仍在图象上即可.‎ ‎(2)①若f(a+x)=f(a-x),x∈R恒成立，‎ 则y=f(x)的图象关于直线x=a对称；‎ ‎②若f(a+x)=-f(a-x),x∈R恒成立，‎ 则y=f(x)的图象关于点(a,0)对称.‎ ‎【探究创新】‎ ‎【解析】由(1)知，-3≤x≤1,-2≤x+1≤2,故f(x)的定义域是［-2，2］.‎ 由(3)知，f(x)在［-2，0)上是增函数.‎ 综合(2)和(4)知，f(x)在(0，2］上也是增函数，且f(-1)=-f(1)=0,f(0)=0.‎ 故函数y=f(x)的一个图象如图所示，与之相应的函数解析式是