2018-2019学年甘肃省张掖二中高二上学期10月月考数学试题（优才）（Word版） 8页

张掖二中2018—2019学年度第一学期月考试卷（10月）‎ 高二数学（优才）‎ 命题人：张志霞 ‎1．设m∈R, 命题“若m>0，则方程x2＋x－m＝0有实根”的逆否命题是(　　)‎ A．若方程x2＋x－m＝0有实根，则m＞0‎ B．若方程x2＋x－m＝0有实根，则m≤0‎ C．若方程x2＋x－m＝0没有实根，则m＞0‎ D．若方程x2＋x－m＝0没有实根，则m≤0‎ ‎2．命题“∃x0∈(0，＋∞)，ln x0＝x0－1”的否定是 (　　)‎ A．∀x∈(0，＋∞)，ln x≠x－1‎ B．∀x∉(0，＋∞)，ln x＝x－1‎ C．∃x0∈(0，＋∞)，ln x0≠x0－1‎ D．∃x0∉(0，＋∞)，ln x0＝x0－1‎ ‎3．阅读如图所示的程序框图，运行相应的程序，若输入x的值为1，‎ 则输出y的值为(　　)‎ A．2 B．7 ‎ C．8 D．128‎ ‎4．函数f(x)＝log2(x2＋2x－3)的定义域是(　 　)‎ A．[－3，1] ‎ B．(－3，1)‎ C．(－∞，－3]∪[1，＋∞) ‎ D．(－∞，－3)∪(1，＋∞)‎ ‎5．已知椭圆＋＝1(m>0)的左焦点为F1(－4,0)，则m＝(　　)‎ A．2　　　　 B．3　　　　 C．4　　　　 D．9‎ ‎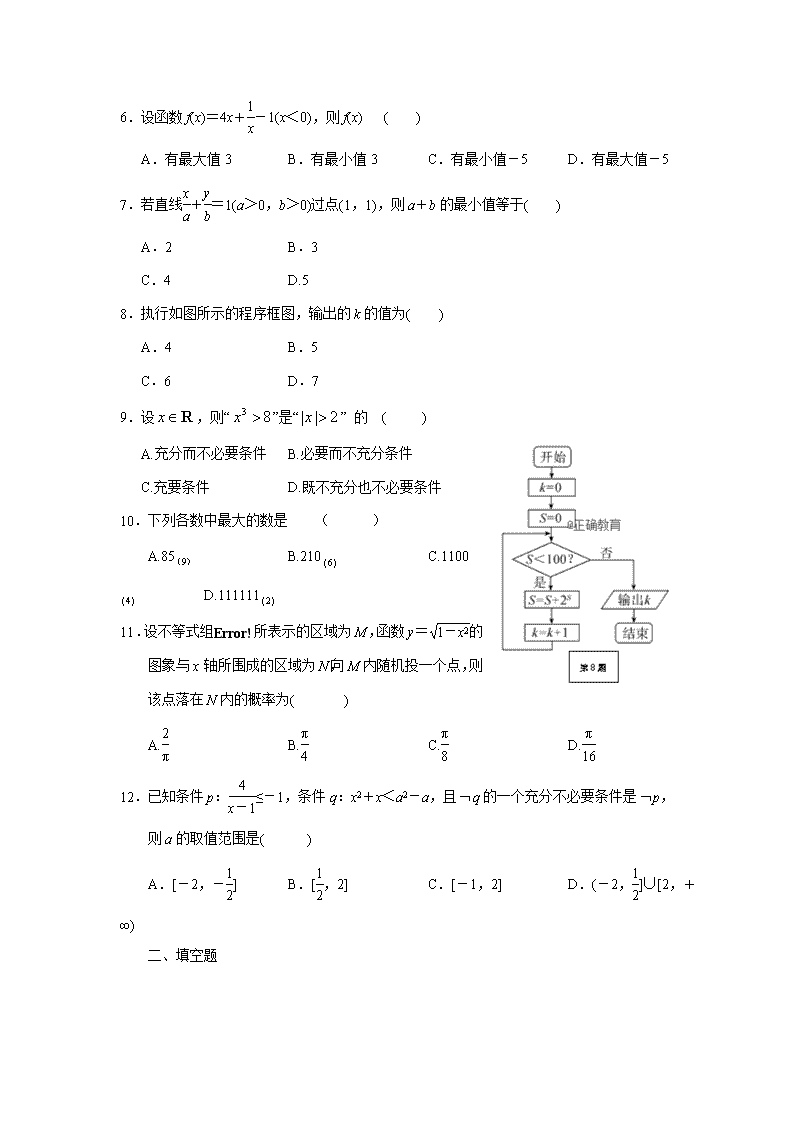6．设函数f(x)＝4x＋－1(x＜0)，则f(x) (　　)‎ A．有最大值3 B．有最小值3 C．有最小值－5 D．有最大值－5‎ ‎7．若直线＋＝1(a＞0，b＞0)过点(1，1)，则a＋b的最小值等于(　　)‎ A．2　　　　 B．3 ‎ C．4 D.5‎ ‎8．执行如图所示的程序框图，输出的k的值为(　　)‎ A．4 B．5 ‎ C．6 D．7‎ ‎9．设，则“”是“” 的 ( )‎ A.充分而不必要条件 B.必要而不充分条件 ‎ C.充要条件 D.既不充分也不必要条件 ‎10．下列各数中最大的数是 （ ）‎ A.85 B.210 C.1100 D.111111‎ ‎11．设不等式组所表示的区域为M，函数y＝的图象与x轴所围成的区域为N，向M内随机投一个点，则该点落在N内的概率为(　 　)‎ A. B. C. D. ‎12．已知条件p：≤－1，条件q：x2＋x＜a2－a，且q的一个充分不必要条件是p，则a的取值范围是(　 　)‎ A．[－2，－]　　 B．[，2] C．[－1，2] D．(－2，]∪[2，＋∞)‎ 二、填空题 ‎13．若满足约束条件 则的最小值是__________‎ ‎14．已知x＞0，y＞0，且＋＝1，若x＋2y＞m2＋2m恒成立，则实数m的取值范围是______．‎ ‎15．已知a，b∈R，且a–3b+6=0，则2a+的最小值为__________．‎ ‎16．已知a∈R，函数若对任意x∈［–3，+），f(x)≤恒成立，则a的取值范围是__________．‎ 三、解答题 ‎17．设命题p：，命题q：x2－(2a＋1)x＋a(a＋1)≤0.若p是q的充分不必要条件，求实数a的取值范围．‎ ‎18．某城市100户居民的月平均用电量(单位：度)，以[160,180)，[180,200)，[200,220)，[220,240)，[240,260)，[260,280)，[280,300]分组的频率分布直方图如图．‎ ‎(1) 求直方图中x的值；‎ ‎(2) 求月平均用电量的众数和中位数；‎ ‎(3) 在月平均用电量为[220,240)，[240,260)，[260,280)，[280,300]的四组用户中，用分层抽 样的方法抽取11户居民，则月平均用电量在[220,240)的用户中应抽取多少户？‎ ‎19．已知某校甲、乙、丙三个年级的学生志愿者人数分别为240，160，160．现采用分层抽样的方法从中抽取７名同学去某敬老院参加献爱心活动．‎ ‎（Ⅰ）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人？‎ ‎（Ⅱ）设抽出的7名同学分别用A，B，C，D，E，F，G表示，现从中随机抽取2名同学承 担敬老院的卫生工作．‎ ‎（i）试用所给字母列举出所有可能的抽取结果；‎ ‎（ii）设M为事件“抽取的2名同学来自同一年级”，求事件M发生的概率．‎ ‎20．某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了‎12月1日至‎12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：‎ 日期 ‎12月1日 ‎12月2日 ‎12月3日 ‎12月4日 ‎12月5日 温差x/摄氏度 ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ 发芽数y/颗 ‎23‎ ‎25‎ ‎30‎ ‎26‎ ‎16‎ 该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求线性回归方 程，再用被选取的2组数据进行检验。‎ ‎（Ⅰ）求选取的2组数据恰好是不相邻2天的数据的概率；‎ ‎（Ⅱ）若选取的是12月1日与12月5日的2组数据，请根据12月2日至4‎ 日的数据，求出 y关于x的线性回归方程，并判断该线性回归方程是否可靠（若由线性回归 方程得到的估计数据与所选取的检验数据的误差均不超过2颗，则认为得到的线性回 归方程是可靠的）。‎ ‎（,）‎ ‎21．设椭圆 的右顶点为A，上顶点为B.已知椭圆的离心率为，‎ ‎.‎ ‎（I）求椭圆的方程；‎ ‎（II）设直线与椭圆交于两点，与直线交于点M，且点P，M均 在第四象限.若的面积是面积的2倍，求k的值.‎ ‎22．已知二次函数满足，且对一切实数恒成立. ‎ 求； ‎ 求的解析式；‎ 求证：‎ 张掖二中2018—2019学年度第一学期月考试卷（10月）‎ 高二数学（优才）答案 ‎1-5:DACDB 6-10:DCAAC 11-12:BC 13. ‎ -2 14. (－4，2) 15. 16.［，2］‎ 17. ‎【解析】　由，得(2x－1)(x－1)<0，解得