2019届二轮复习立体几何课件（37张）（全国通用） 37页

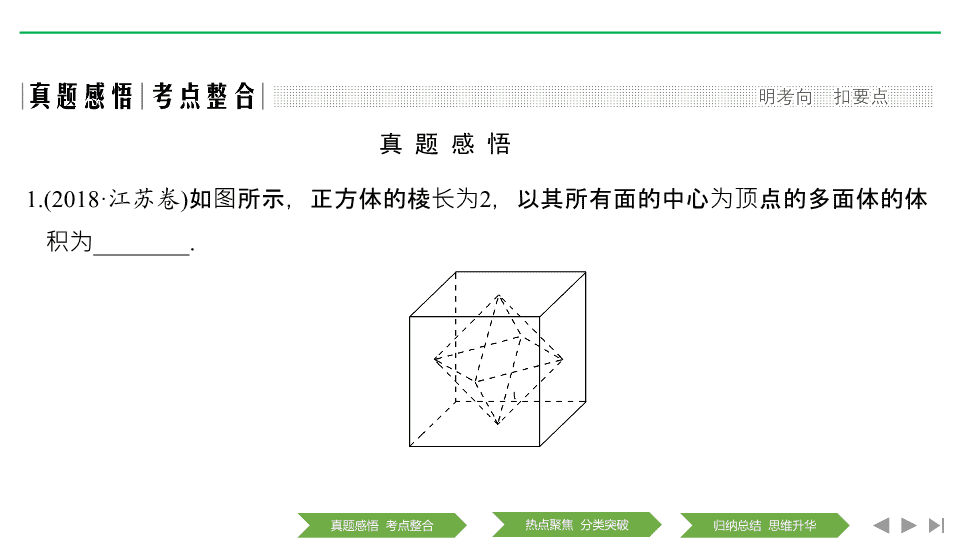
高考定位　 高考对本内容的考查主要有： (1) 空间概念、空间想象能力、点线面位置关系判断、表面积与体积计算等， A 级要求； (2) 线线、线面、面面平行与垂直的证明， B 级要求 . 1. (2018· 江苏卷 ) 如图所示，正方体的棱长为 2 ，以其所有面的中心为顶点的多面体的体积为 ________. 真 题 感 悟 因为 AB  平面 A 1 B 1 C ， A 1 B 1  平面 A 1 B 1 C ，所以 AB ∥ 平面 A 1 B 1 C . (2) 在平行六面体 ABCD － A 1 B 1 C 1 D 1 中，四边形 ABB 1 A 1 为平行四边形 . 又因为 AA 1 ＝ AB ，所以四边形 ABB 1 A 1 为菱形，因此 AB 1 ⊥ A 1 B . 又因为 AB 1 ⊥ B 1 C 1 ， BC ∥ B 1 C 1 ，所以 AB 1 ⊥ BC . 又因为 A 1 B ∩ BC ＝ B ， A 1 B  平面 A 1 BC ， BC  平面 A 1 BC ，所以 AB 1 ⊥ 平面 A 1 BC . 因为 AB 1  平面 ABB 1 A 1 ，所以平面 ABB 1 A 1 ⊥ 平面 A 1 BC . 3. (2017· 江苏卷 ) 如图，在三棱锥 A － BCD 中， AB ⊥ AD ， BC ⊥ BD ，平面 ABD ⊥ 平面 BCD ，点 E ， F ( E 与 A ， D 不重合 ) 分别在棱 AD ， BD 上，且 EF ⊥ AD . 求证： (1) EF ∥ 平面 ABC ； (2) AD ⊥ AC . 证明　 (1) 在平面 ABD 内，因为 AB ⊥ AD ， EF ⊥ AD ，所以 EF ∥ AB . 又因为 EF  平面 ABC ， AB  平面 ABC ，所以 EF ∥ 平面 ABC . (2) 因为平面 ABD ⊥ 平面 BCD ，平面 ABD ∩ 平面 BCD ＝ BD ， BC  平面 BCD ， BC ⊥ BD ，所以 BC ⊥ 平面 ABD . 因为 AD  平面 ABD ， 所以 BC ⊥ AD . 又 AB ⊥ AD ， BC ∩ AB ＝ B ， AB  平面 ABC ， BC  平面 ABC ， 所以 AD ⊥ 平面 ABC ，又因为 AC  平面 ABC ，所以 AD ⊥ AC . 4. (2016· 江苏卷 ) 如图，在直三棱柱 ABC － A 1 B 1 C 1 中， D ， E 分别为 AB ， BC 的中点，点 F 在侧棱 B 1 B 上，且 B 1 D ⊥ A 1 F ， A 1 C 1 ⊥ A 1 B 1 . 求证： (1) 直线 DE ∥ 平面 A 1 C 1 F ； (2) 平面 B 1 DE ⊥ 平面 A 1 C 1 F . 证明 　 (1) 在直三棱柱 ABC － A 1 B 1 C 1 中， A 1 C 1 ∥ AC . 在 △ ABC 中，因为 D ， E 分别为 AB ， BC 的中点，所以 DE ∥ AC ，于是 DE ∥ A 1 C 1 . 又 DE  平面 A 1 C 1 F ， A 1 C 1  平面 A 1 C 1 F ，所以直线 DE ∥ 平面 A 1 C 1 F . (2) 在直三棱柱 ABC － A 1 B 1 C 1 中， A 1 A ⊥ 平面 A 1 B 1 C 1 . 因为 A 1 C 1  平面 A 1 B 1 C 1 ，所以 A 1 A ⊥ A 1 C 1 . 又 A 1 C 1 ⊥ A 1 B 1 ， A 1 A  平面 ABB 1 A 1 ， A 1 B 1  平面 ABB 1 A 1 ， A 1 A ∩ A 1 B 1 ＝ A 1 ， 所以 A 1 C 1 ⊥ 平面 ABB 1 A 1 . 因为 B 1 D  平面 ABB 1 A 1 ，所以 A 1 C 1 ⊥ B 1 D . 又 B 1 D ⊥ A 1 F ， A 1 C 1  平面 A 1 C 1 F ， A 1 F  平面 A 1 C 1 F ， A 1 C 1 ∩ A 1 F ＝ A 1 ， 所以 B 1 D ⊥ 平面 A 1 C 1 F . 因为直线 B 1 D  平面 B 1 DE ， 所以平面 B 1 DE ⊥ 平面 A 1 C 1 F . 1. 四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系 . 考 点 整 合 2. 空间几何体的两组常用公式 3. 直线、平面平行的判定及其性质 (1) 线面平行的判定定理： a  α ， b  α ， a ∥ b  a ∥ α . (2) 线面平行的性质定理： a ∥ α ， a  β ， α ∩ β ＝ b  a ∥ b . (3) 面面平行的判定定理： a  β ， b  β ， a ∩ b ＝ P ， a ∥ α ， b ∥ α  α ∥ β . (4) 面面平行的性质定理： α ∥ β ， α ∩ γ ＝ a ， β ∩ γ ＝ b  a ∥ b . 4. 直线、平面垂直的判定及其性质 (1) 线面垂直的判定定理： m  α ， n  α ， m ∩ n ＝ P ， l ⊥ m ， l ⊥ n  l ⊥ α . (2) 线面垂直的性质定理： a ⊥ α ， b ⊥ α  a ∥ b . (3) 面面垂直的判定定理： a  β ， a ⊥ α  α ⊥ β . (4) 面面垂直的性质定理： α ⊥ β ， α ∩ β ＝ l ， a  α ， a ⊥ l  a ⊥ β . 热点一　空间几何体的有关计算 (2) (2018· 徐州、连云港、宿迁三检 ) 在三棱柱 ABC － A 1 B 1 C 1 中，侧棱 AA 1 ⊥ 平面 AB 1 C 1 ， AA 1 ＝ 1 ，底面三角形 ABC 是边长为 2 的正三角形，则此三棱柱的体积为 ________. 探究提高 　 (1) 涉及柱、锥及其简单组合体的计算问题，要在正确理解概念的基础上，画出符合题意的图形或辅助线 ( 面 ) ，再分析几何体的结构特征，从而进行解题 . (2) 求三棱锥的体积，等体积转化是常用的方法，转换原则是其高易求，底面放在已知几何体的某一面上 . (3) 若所给的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法求解 . (3) (2018· 苏州调研 ) 将半径为 5 的圆分割成面积之比为 1 ∶ 2 ∶ 3 的三个扇形作为三个圆锥的侧面，设这三个圆锥的底面半径依次为 r 1 ， r 2 ， r 3 ，则 r 1 ＋ r 2 ＋ r 3 ＝ ________. 热点二　空间中的平行和垂直的判断与证明 [ 考法 1] 　空间线面位置关系的判断 【例 2 － 1 】 (1)( 2017· 南京、盐城模拟 ) 设 α ， β 为两个不同的平面， m ， n 为两条不同的直线，下列命题中正确的是 ________( 填上所有正确命题的序号 ). ① 若 α ∥ β ， m  α ，则 m ∥ β ； ② 若 m ∥ α ， n  α ，则 m ∥ n ； ③ 若 α ⊥ β ， α ∩ β ＝ n ， m ⊥ n , 则 m ⊥ β ； ④ 若 n ⊥ α ， n ⊥ β ， m ⊥ α ，则 m ⊥ β . (2) (2018· 镇江期末 ) 设 b ， c 表示两条直线， α ， β 表示两个平面，现给出下列命题： ① 若 b  α ， c ∥ α ，则 b ∥ c ； ② 若 b  α ， b ∥ c ，则 c ∥ α ； ③ 若 c ∥ α ， α ⊥ β ，则 c ⊥ β ； ④ 若 c  α ， c ⊥ β ，则 α ⊥ β . 其中正确的命题是 ________( 写出所有正确命题的序号 ). 解析　 (1) 由面面平行的性质可得 ① 正确；若 m ∥ α ， n  α ，则 m ， n 平行或异面， ② 错误；由面面垂直的性质定理可知 ③ 中缺少条件 “ m  α ” ， ③ 错误；若 n ⊥ α ， n ⊥ β ，则 α ∥ β ，又 m ⊥ α ，则 m ⊥ β ， ④ 正确 . 综上，命题正确的是 ①④ . (2) ① b 和 c 可能异面，故 ① 错； ② 可能 c  α ，故 ② 错； ③ 可能 c ∥ β ， c  β ，故 ③ 错； ④ 根据面面垂直判定定理判定 α ⊥ β ，故 ④ 正确 . 答案 　 (1) ①④ 　 (2) ④ 探究提高 　 长方体 ( 或正方体 ) 是一类特殊的几何体，其中蕴含着丰富的空间位置关系 . 因此，对于某些研究空间直线与直线、直线与平面、平面与平面之间的平行、垂直关系问题，常构造长方体 ( 或正方体 ) ，把点、线、面的位置关系转移到长方体 ( 或正方体 ) 中，对各条件进行检验或推理，根据条件在某一特殊情况下不真，则它在一般情况下也不真的原理，判断条件的真伪，可使此类问题迅速获解 . [ 考法 2] 　平行、垂直关系的证明 【例 2 － 2 】 (2015· 江苏卷 ) 如图，在直三棱柱 ABC － A 1 B 1 C 1 中，已知 AC ⊥ BC ， BC ＝ CC 1 . 设 AB 1 的中点为 D ， B 1 C ∩ BC 1 ＝ E . 求证： (1) DE ∥ 平面 AA 1 C 1 C ； (2) BC 1 ⊥ AB 1 . 证明　 (1) 由题意知， E 为 B 1 C 的中点，又 D 为 AB 1 的中点，因此 DE ∥ AC . 又因为 DE  平面 AA 1 C 1 C ， AC  平面 AA 1 C 1 C ，所以 DE ∥ 平面 AA 1 C 1 C . (2) 因为棱柱 ABC － A 1 B 1 C 1 是直三棱柱，所以 CC 1 ⊥ 平面 ABC . 因为 AC  平面 ABC ，所以 AC ⊥ CC 1 . 又因为 AC ⊥ BC ， CC 1  平面 BCC 1 B 1 ， BC  平面 BCC 1 B 1 ， BC ∩ CC 1 ＝ C ， 所以 AC ⊥ 平面 BCC 1 B 1 . 又因为 BC 1  平面 BCC 1 B 1 ，所以 BC 1 ⊥ AC . 因为 BC ＝ CC 1 ，所以矩形 BCC 1 B 1 是正方形，因此 BC 1 ⊥ B 1 C . 因为 AC ， B 1 C  平面 B 1 AC ， AC ∩ B 1 C ＝ C ，所以 BC 1 ⊥ 平面 B 1 AC . 又因为 AB 1  平面 B 1 AC ，所以 BC 1 ⊥ AB 1 . 又由 (1) 可得 OP ⊥ CH ， OM ∩ OP ＝ O ， OM ， OP  平面 POM ， 所以 CH ⊥ 平面 POM . 故 CH 的长为点 C 到平面 POM 的距离 . 探究提高 　 垂直、平行关系证明中应用转化与化归思想的常见类型 . (1) 证明线面、面面平行，需转化为证明线线平行 . (2) 证明线面垂直，需转化为证明线线垂直 . (3) 证明线线垂直，需转化为证明线面垂直 . (4) 证明面面垂直，需转化为证明线面垂直，进而转化为证明线线垂直 . 【训练 2 】 (2017· 苏、锡、常、镇调研 ) 如图，在四棱锥 P － ABCD 中， AB ⊥ AC ， AB ⊥ PA ， AB ∥ CD ， AB ＝ 2 CD ， E ， F ， G ， M ， N 分别为 PB ， AB ， BC ， PD ， PC 的中点 . 求证： (1) CE ∥ 平面 PAD ； (2) 平面 EFG ⊥ 平面 EMN . 证明　 (1) 法一　 如图 1 ，取 PA 的中点 H ，连接 EH ， DH . 图 1 所以 EH ∥ CD ，且 EH ＝ CD . 所以四边形 DCEH 是平行四边形 . 所以 CE ∥ DH . 又 DH  平面 PAD ， CE  平面 PAD ，因此， CE ∥ 平面 PAD . 图 2 所以四边形 AFCD 为平行四边形 . 因此 CF ∥ AD . 又 CF  平面 PAD ， AD  平面 PAD ，所以 CF ∥ 平面 PAD . 因为 E ， F 分别为 PB ， AB 的中点，所以 EF ∥ PA . 又 EF  平面 PAD ， PA  平面 PAD ，所以 EF ∥ 平面 PAD . 因为 CF ∩ EF ＝ F ， CF  平面 CEF ， EF  平面 CEF ， 故平面 CEF ∥ 平面 PAD . 又 CE  平面 CEF ，所以 CE ∥ 平面 PAD . (2) 因为 E ， F 分别为 PB ， AB 的中点，所以 EF ∥ PA . 又 AB ⊥ PA ，所以 AB ⊥ EF . 同理可证 AB ⊥ FG . 又 EF ∩ FG ＝ F ， EF  平面 EFG ， FG  平面 EFG ， 因此 AB ⊥ 平面 EFG . 又 M ， N 分别为 PD ， PC 的中点， 所以 MN ∥ DC ，又 AB ∥ DC ，所以 MN ∥ AB ， 所以 MN ⊥ 平面 EFG . 又 MN  平面 EMN ，所以平面 EFG ⊥ 平面 EMN . 1. 求解几何体的表面积或体积 (1) 对于规则几何体，可直接利用公式计算 . (2) 对于不规则几何体，可采用割补法求解；对于某些三棱锥，有时可采用等体积转换法求解 . (3) 求解旋转体的表面积和体积时，注意圆柱的轴截面是矩形，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形的应用 . (4) 求解几何体的表面积时要注意 S 表 ＝ S 侧 ＋ S 底 . 3. 空间中点、线、面的位置关系的判定 (1) 可以从线、面的概念、定理出发，学会找特例、反例 . (2) 可以借助长方体，在理解空间点、线、面位置关系的基础上，抽象出空间线、面的位置关系的定义 . 4. 垂直、平行关系的基础是线线垂直和线线平行，常用方法如下： (1) 证明线线平行常用的方法：一是利用平行公理，即证两直线同时和第三条直线平行；二是利用平行四边形进行平行转换：三是利用三角形的中位线定理证线线平行；四是利用线面平行、面面平行的性质定理进行平行转换 . (2) 证明线线垂直常用的方法： ① 利用等腰三角形底边中线即高线的性质； ② 勾股定理； ③ 线面垂直的性质：即要证两线垂直，只需证明一线垂直于另一线所在的平面即可， l ⊥ α ， a  α  l ⊥ a .