安徽省蚌埠市2020届高三下学期第三次教学质量检查考试 数学（文） 11页

蚌埠市2020届高三年级第三次教学质量检查考试 数学(文史类)‎ 本试卷满分150分，考试时间120分钟 注意事项：‎ ‎1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。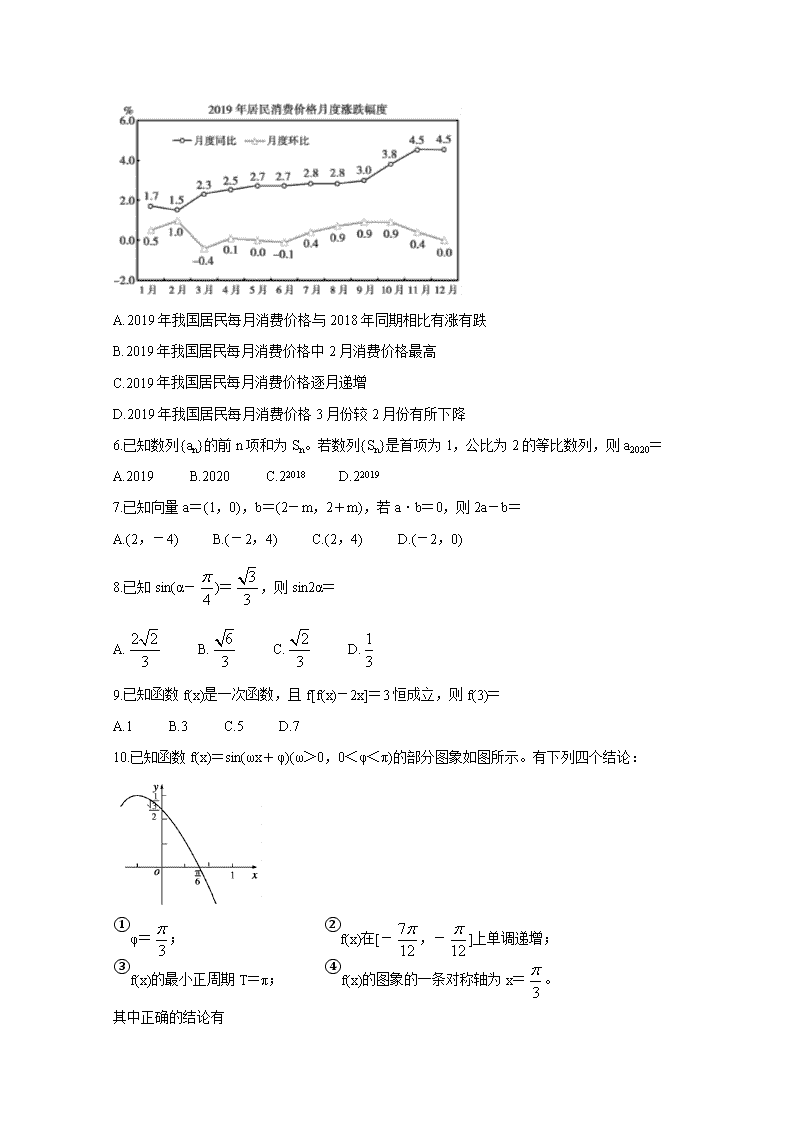‎ ‎1.已知集合A＝{x|x2－5x＜－4}，集合B＝{x|x≤0}，则A∩(B)＝‎ A.(0，4) B.(1，4) C.(－1，4) D.(－1，0)‎ ‎2.已知i为虚数单位，复数z满足(1－i)(z＋i)＝1，则z＝‎ A.－i B.＋i C.1－i D.1＋i ‎3.已知双曲线的离心率为2，则实数m的值为 A.4 B.8 C.12 D.16‎ ‎4.已知直线l，m和平面α，且mα，则“l⊥m”是“l⊥α”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件 ‎5.在统计学中，同比增长率一般是指和去年同期相比较的增长率，环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表，根据2019年居民消费价格月度涨跌幅度统计折线图，下列说法正确的是 A.2019年我国居民每月消费价格与2018年同期相比有涨有跌 B.2019年我国居民每月消费价格中2月消费价格最高 C.2019年我国居民每月消费价格逐月递增 D.2019年我国居民每月消费价格3月份较2月份有所下降 ‎6.已知数列{an}的前n项和为Sn。若数列{Sn}是首项为1，公比为2的等比数列，则a2020＝‎ A.2019 B.2020 C.22018 D.22019‎ ‎7.已知向量a＝(1，0)，b＝(2－m，2＋m)，若a·b＝0，则2a－b＝‎ A.(2，－4) B.(－2，4) C.(2，4) D.(－2，0)‎ ‎8.已知sin(α－)＝，则sin2α＝‎ A. B. C. D.‎ ‎9.已知函数f(x)是一次函数，且f[f(x)－2x]＝3恒成立，则f(3)＝‎ A.1 B.3 C.5 D.7‎ ‎10.已知函数f(x)＝sin(ωx＋φ)(ω＞0，0＜φ＜π)的部分图象如图所示。有下列四个结论：‎ ‎①φ＝； ②f(x)在[－，－]上单调递增；‎ ‎③f(x)的最小正周期T＝π； ④f(x)的图象的一条对称轴为x＝。‎ 其中正确的结论有 A.②③ B.②④ C.①④ D.①②‎ ‎11.足球起源于中国东周时期的齐国，当时把足球称为“蹴鞠”。汉代蹴鞠是训练士兵的手段，制定了较为完备的体制。如专门设置了球场，规定为东西方向的长方形，两端各设六个对称的“鞠域”，也称“鞠室”，各由一人把守。比赛分为两队，互有攻守，以踢进对方鞠室的次数决定胜负。1970年以前的世界杯用球多数由举办国自己设计，所以每一次球的外观都不同，拼块的数目如同掷骰子一样没准。自1970年起，世界杯官方用球选择了三十二面体形状的足球，沿用至今。如图Ⅰ，三十二面体足球的面由边长相等的12块正五边形和20块正六边形拼接而成，形成一个近似的球体.现用边长为4.5cm的上述正五边形和正六边形所围成的三十二面体的外接球作为足球，其大圆圆周展开图可近似看成是由4个正六边形与4个正五边形以及2条正六边形的边所构成的图形的对称轴截图形所得的线段AA′，如图Ⅱ，则该足球的表面积约为 参考数据：tan72°≈3.08，≈1.73，π≈3.14，67.862≈4604.98。‎ A.366.64cm2 B.488.85cm2 C.1466.55cm2 D.5282.40cm2‎ ‎12.已知函数。若函数g(x)＝－x＋m(m＞0)与y＝f(x)的图象相交于A，B两点，且A，B两点的横坐标分别记为x1，x2，则x1＋x2的取值范围是 A.(1，) B.[log23，) C.[1，) D.[log23，3]‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.曲线f(x)＝exsinx在点(0，0)处的切线方程为 。‎ ‎14.已知等差数列{an}的前n项和为Sn。若a3＝36，an－2＝6，Sn＝126，则n＝ 。‎ ‎15.某企业为了调查其产品在国内和国际市场的发展情况，随机抽取国内、国外各100名客户代表，了解他们对该企业产品的发展前景所持的态度，得到如图所示的等高条形图，则 ‎ ‎ (填“能”或“不能”)有99％以上的把握认为是否持乐观态度与国内外差异有关。‎ 附：。‎ ‎16.已知点P(，1)，M，N是椭圆上的两个动点，记直线PM，PN，MN的斜率分别为k1，k2，k，若k1＋k2＝0，则k＝ 。‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎(一)必考题：共60分。‎ ‎17.(12分)‎ 如图所示，△ABC的内角A，B，C所对的边分别为a，b，c，且cosC－sinC＝。‎ ‎(1)求A；‎ ‎(2)若点P是线段CA延长线上一点，且PA＝3，AC＝2，C＝，求PB。‎ ‎18.(12分)‎ 随着网购人数的日益增多，网上的支付方式也呈现一种多样化的状态，越来越多的便捷移动支付方式受到了人们的青睐，更被网友们评为“新四大发明”之一.随着人们消费观念的进步，许多人喜欢用信用卡购物，考虑到这一点，一种“网上的信用卡”横空出世－－蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式，简单便捷，同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系，某网站对其注册用户开展抽样调查，在每个年龄段的注册用户中各随机抽取100人，得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如下图所示。‎ ‎(1)由大数据可知，在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系，利用统计图表中的数据，以各年龄段的区间中点代表该年龄段的年龄，求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程(回归直线方程的斜率和截距保留两位有效数字)；‎ ‎(2)该网站年龄为20岁的注册用户共有2000人，试估算该网站20岁的注册用户中使用花呗“赊购”的人数；‎ ‎(3)已知该网店中年龄段在18－26岁和27－35岁的注册用户人数相同，现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人，再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度，求抽取的两人年龄都在18到26岁的概率。‎ 参考公式：‎ ‎19.(12分)‎ 如图所示七面体中，AA1//BB1//DD1，AA1⊥平面ABED，平面A1B1C1D1//平面ABED，四边形A1B1C1D1是边长为2的菱形，∠D1A1B1＝60°，AA1＝2A1B1＝4BE，M，N分别为A1D，BB1的中点。‎ ‎(1)求证：MN//平面C1DE；‎ ‎(2)求三棱锥M－C1DE的体积。‎ ‎20.(12分)‎ 已知函数f(x)＝alnx＋x2－3x＋k。‎ ‎(1)当a＞0时，求函数f(x)的极值点；‎ ‎(2)当a＝1时，对任意的x∈[，e]，f(x)≤0恒成立，求实数k的取值范围。‎ ‎21.(12分)‎ 如图，设抛物线C1：x2＝4y与抛物线C2：y2＝2px(p＞0)在第一象限的交点为M(t，)，点A，B分别在抛物线C2，C1上，AM，BM分别与C2，C1相切。‎ ‎ ‎ ‎(1)当点M的纵坐标为4时，求抛物线C2的方程；‎ ‎(2)若t∈[1，2]，求△MBA面积的取值范围。‎ ‎(二)选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22.[选修4－4：坐标系与参数方程](10分)‎ 在平面直角坐标系xOy中，直线l的参数方程为，(其中t为参数，≤α＜π)。在以原点O为极点，x轴的非负半轴为极轴所建立的极坐标系中，曲线C的极坐标方程为ρcos2θ＝2cosθ－2ρsin2θ。设直线l与曲线C相交于A，B两点。‎ ‎(1)求曲线C和直线l的直角坐标方程；‎ ‎(2)已知点P(0，1)，求的最大值。‎ ‎23.[选修4－5：不等式选讲](10分)‎ 已知函数f(x)＝|x－m|＋|x|，x∈R。‎ ‎(1)若不等式f(x)≥m2对x∈R恒成立，求实数m的取值范围；‎ ‎(2)若(1)中实数m的最大值为t，且a＋b＋c＝t(a，b，c均为正实数)。‎ 证明：≥9。‎