黑龙江省大庆实验中学2020届高三下学期“战疫”线上教学综合测试数学（理）试题 5页

理 科 数 学 注意事项：‎ ‎1．答案要按时上传到美师优课。‎ ‎2．填空、解答题整道题拍照上传，答案写在答题卡对应位置上，拍照一定要尽可能的清晰。‎ ‎3．解答题多数都是两个问，请拍成一张上传到美师优课，别分成两个问上传，容易看不到，漏批。‎ 一、选择题（本大题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1． （ ）‎ A．1-i B．2-2i C．1+i D．2+2i ‎ ‎2．设集合,则的子集的个数是 （ ）‎ A．8 B．‎4 ‎ C．2 D．0‎ ‎3.《张丘建算经》是中国古代的数学著作，书中有一道题为：“今有女善织，日益功疾（注：从第2天开始，每天比前一天多织相同量的布），第一天织5尺布，现一月（按30天计）共织390尺布”，则第30天织布 （ ）‎ A．7尺 B．14尺 C．21尺 D．28尺 ‎4．以下四个结论，正确的是 （ ）‎ ‎①质检员从匀速传递的产品生产流水线上，每间隔15分钟抽取一件产品进行某项指标检测，这样的抽 样是分层抽样；‎ ‎②在回归直线方程中，当变量x每增加一个单位时，变量增加0.13个单位；‎ ‎③在频率分布直方图中，所有小矩形的面积之和是1；‎ ‎④对于两个分类变量X与Y，求出其统计量的观测值k，观测值k越大，我们认为“X与Y有关系”的 把握程度就越大.‎ A．②④ B．②③ C．①③ D．③④‎ ‎5．在的展开式中的系数是 （ ）‎ A．－14 B．‎14 ‎ C．-28 D．28‎ ‎6．抛物线的焦点为,准线为,,是抛物线上的两个动点,且满足,设线段的中点在上的投影为,则的最大值是 （ ）‎ A． B． C． D．‎ ‎7．设是两条不同直线，是两个不同的平面，下列命题正确的是 （ ）‎ A． B．，则 C．，那么 D．‎ ‎8．已知双曲线的中心在原点,一个焦点为,点在双曲线上,且线段的中点坐标为,则此双曲线的方程是 （ ）‎ A． B． C． D． ‎ ‎9．已知向量与向量共线，其中是的内角，则角的大小为 （ ）‎ A． B． C． D．‎ ‎10．已知在上是可导函数,则的图象如图所示，则不等式的解集为（ ）‎ A． B． C． D． ‎ ‎11．已知正四面体的棱长为，则其外接球的体积为 （ ）‎ A． B． C． D． ‎ ‎12．已知椭圆与双曲线有相同的焦点，则双曲线的一条斜率为正的渐近线的斜率的取值范围为 （ ）‎ A． B． C． D．‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．某校从高一年级学生中随机抽取部分学生，将他们的数学检测成绩（满 ‎ 分100分）分成6组：[40,50), [50,60), [60,70), [70,80), [80,90), [90,100]‎ 加以统计，得到如图所示的频率分布直方图。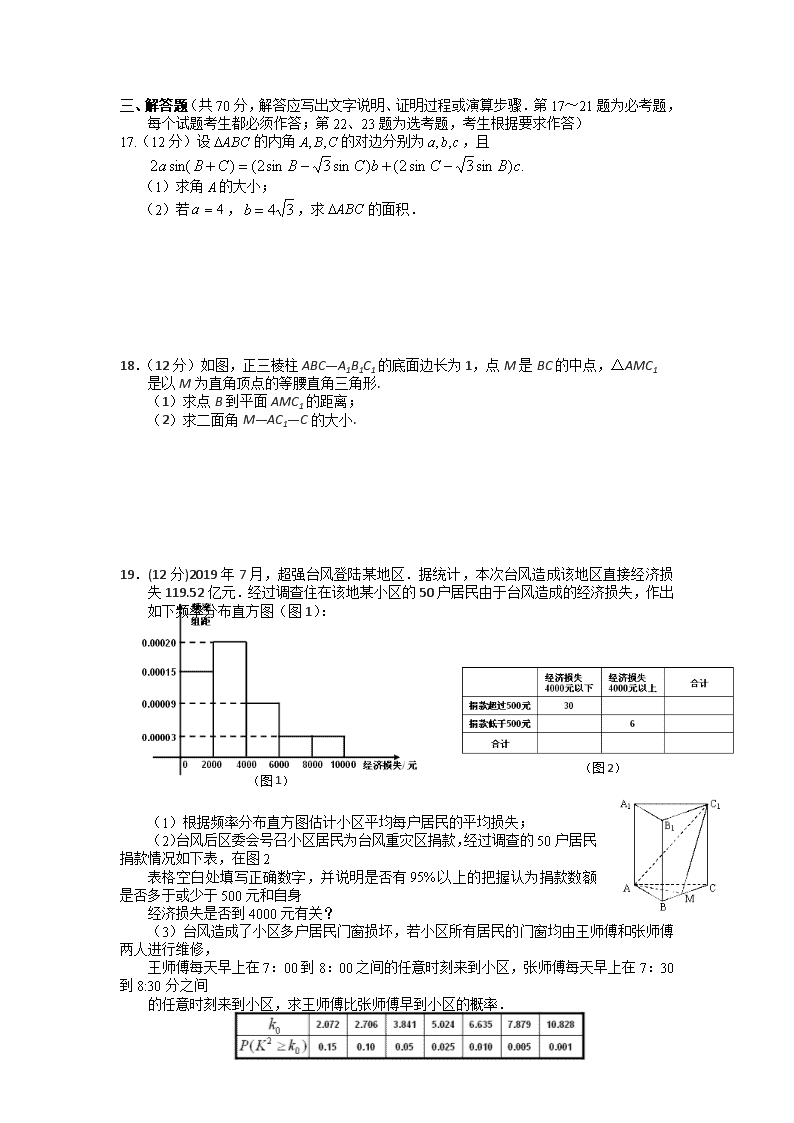已知高一年级共有学生 ‎800名，据此估计，该数学检测成绩不少于60分的学生人数为_______‎ 人.‎ ‎14．在等比数列中，,则数列的前n项和为___________.‎ ‎15．在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被5整除的数共有___________个.（用数字作答）‎ ‎16．设是数列的前n项和，且，，则________．‎ 三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答；第22、23题为选考题，考生根据要求作答）‎ ‎17.（12分）设的内角的对边分别为，且 ‎（1）求角的大小；‎ ‎（2）若，，求的面积．‎ ‎18．（12分）如图，正三棱柱ABC—A1B‎1C1的底面边长为1，点M是BC的中点，△AMC1‎ 是以M为直角顶点的等腰直角三角形.‎ ‎ （1）求点B到平面AMC1的距离；‎ ‎ （2）求二面角M—AC1—C的大小.‎ ‎（图1）‎ ‎19．(12分)2019年7月，超强台风登陆某地区．据统计，本次台风造成该地区直接经济损失119.52亿元．经过调查住在该地某小区的50户居民由于台风造成的经济损失，作出如下频率分布直方图（图1）：‎ ‎（图2）‎ ‎（1）根据频率分布直方图估计小区平均每户居民的平均损失；‎ ‎（2）台风后区委会号召小区居民为台风重灾区捐款，经过调查的50户居民捐款情况如下表，在图2‎ 表格空白处填写正确数字，并说明是否有以上的把握认为捐款数额是否多于或少于500元和自身 经济损失是否到4000元有关？‎ ‎（3）台风造成了小区多户居民门窗损坏，若小区所有居民的门窗均由王师傅和张师傅两人进行维修，‎ 王师傅每天早上在7：00到8：00之间的任意时刻来到小区，张师傅每天早上在7：30到8:30分之间 的任意时刻来到小区，求王师傅比张师傅早到小区的概率．‎ 附：临界值表 参考公式：，．‎ ‎20.（12分）已知动圆M过定点F（0，-1），且与直线：y=1相切，椭圆C2的对称轴为坐标轴，O点为坐 标原点，F是其一个焦点，又点A（0，2）在椭圆C2上． （1）求动圆圆心M的轨迹C1的标准方程和椭圆C2的标准方程； （2）若过F的动直线m交椭圆C2于B，C点，交轨迹C1于D，E两点，设S1为△ABC的面积，S2为△‎ ODE的面积，令Z=S1S2，试求Z的取值范围．‎ ‎21.（12分）已知函数.‎ ‎（1）设实数（为自然对数的底数），求函数在上的最小值； ‎ ‎（2）若为正整数，且对任意恒成立，求的最大值．‎ 请考生在第22、23题中任选一题作答；如果多做，则按所做的第一题计分。‎ ‎22．[选修4－4：坐标系与参数方程]（10分）在平面直角坐标系中，过点作倾斜角为的直线，以原点O为极点，x轴非负半轴为极轴建立极坐标系，曲线C1的极坐标方程为，将曲线C1上各点的横坐标伸长为原来的2倍，纵坐标不变，得到曲线C2，直线与曲线C2交于不同的两点M，N.‎ ‎ （1）求直线的参数方程和曲线C2的普通方程；‎ ‎ （2）求的值。‎ ‎23．[选修4—5：不等式选讲]（10分）设函数。‎ ‎（1）若a=l，解不等式;‎ ‎（2）若函数f（x）有最小值，求实数a的取值范围.‎