2019届二轮复习（理）不等式选讲学案（全国通用） 17页

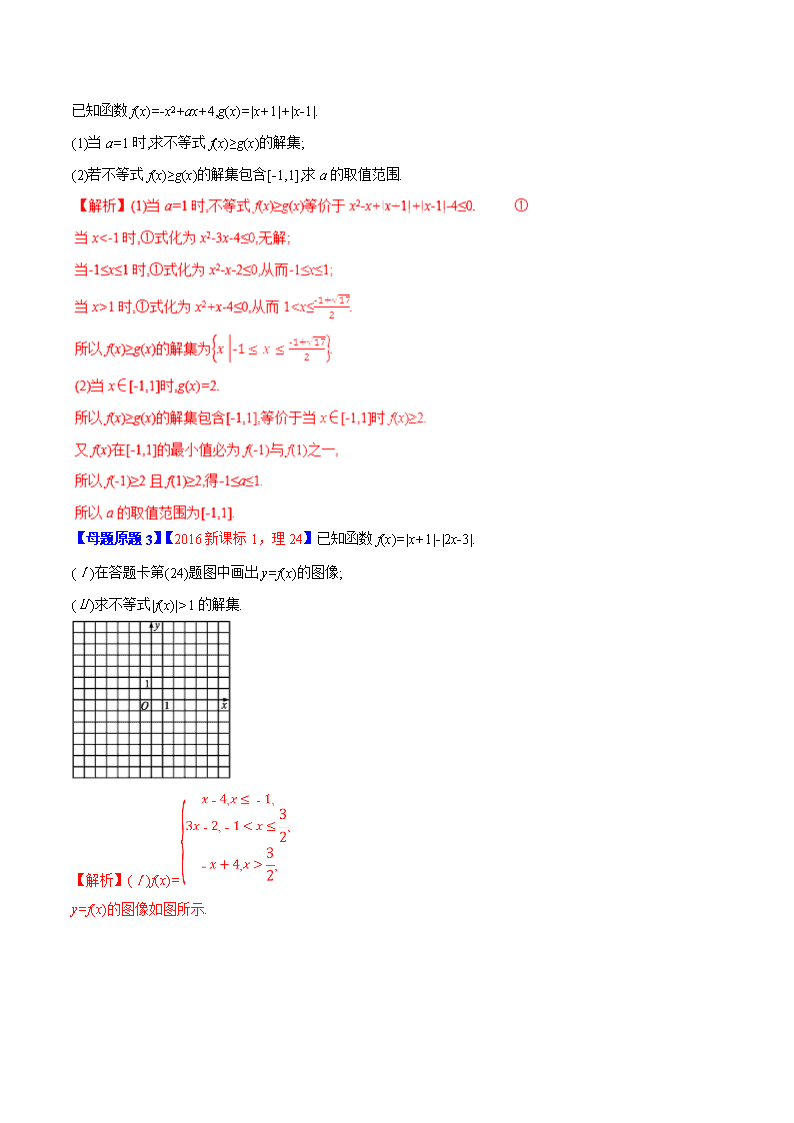
‎【母题原题1】【2018新课标1，理23】已知.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若时不等式成立，求的取值范围.‎ 点睛：该题考查的是有关绝对值不等式的解法，以及含参的绝对值的式子在某个区间上恒成立求参数的取值范围的问题，在解题的过程中，需要会用零点分段法将其化为分段函数，从而将不等式转化为多个不等式组来解决，关于第二问求参数的取值范围时，可以应用题中所给的自变量的范围，去掉一个绝对值符号，之后进行分类讨论，求得结果.‎ ‎【母题原题2】【2017新课标1，理23】‎ 已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.‎ ‎(1)当a=1时,求不等式f(x)≥g(x)的解集;‎ ‎(2)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.‎ ‎【母题原题3】【2016新课标1，理24】已知函数f(x)=|x+1|-|2x-3|.‎ ‎(Ⅰ)在答题卡第(24)题图中画出y=f(x)的图像;‎ ‎(Ⅱ)求不等式|f(x)|>1的解集.‎ ‎【解析】(Ⅰ)f(x)= . ]‎ y=f(x)的图像如图所示. ‎ ‎【绝对值不等式的解法与性质】‎ ‎1．|ax＋b|≤c，|ax＋b|≥c型不等式的解法 ‎（1）若c>0，则|ax＋b|≤c⇔–c≤ax＋b≤c，|ax＋b|≥c⇔ax＋b≥c或ax＋b≤–c，然后根据a，b的取值求解即可；‎ ‎（2）若c<0，则|ax＋b|≤c的解集为∅，|ax＋b|≥c的解集为R．‎ ‎2．|x–a|＋|x–b|≥c，|x–a|＋|x–b|≤c（c>0）型不等式的解法 零点分区间法 零点分区间法的一般步骤为：‎ ‎①令每个绝对值符号内的代数式为零，并求出相应的根；‎ ‎②将这些根按从小到大排序，并把实数集分成若干个区间；‎ ‎③由所分区间去掉绝对值符号组成若干个不等式，解这些不等式，求出解集；‎ ‎④取各个不等式解集的并集即可得到原不等式的解集．‎ 几何法（利用|x–a|的几何意义）‎ 由于|x–a|+|x–b|与|x–a|–|x–b|分别表示数轴上与x对应的点到与a，b对应的点的距离之和与距离之差，因此对形如|x–a|+|x–b|≤c（c>0）或|x–a|–|x–b|≥c（c>0）的不等式，利用绝对值的几何意义求解更直观．‎ 数形结合法 通过构造函数，利用函数的图象求解，体现函数与方程的思想，正确求出函数的零点并画出函数图象是解题的关键．‎ ‎3．|f（x）|>g（x），|f（x）|0）型不等式的解法：‎ ‎①|f（x）|>g（x）⇔f（x）>g（x）或f（x）<–g（x）；‎ ‎②|f（x）|