2018届二轮复习规范答题大题突破课立体几何课件理 42页

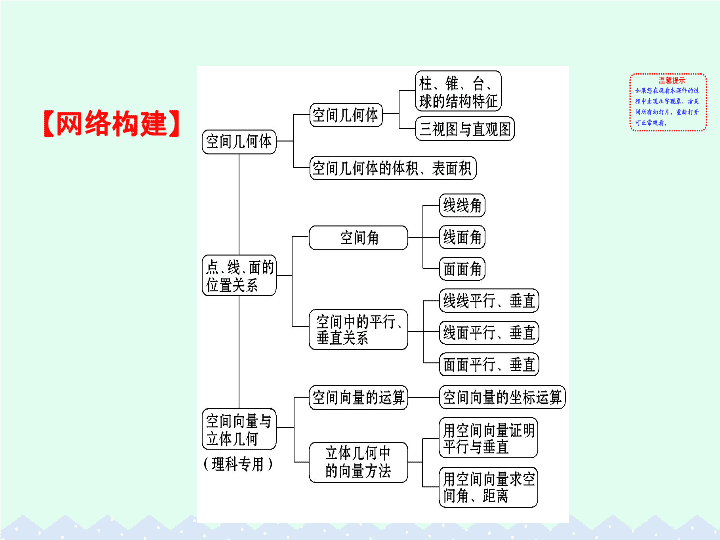
阶段总结 · 热考题型强化课 ( 四 ) 立体几何 【 网络构建 】 【 核心要素 】 1. 空间几何体的结构 2. 三视图、直观图 3. 空间几何体的表面积、体积的计算 4. 异面直线所成的角、线面角、二面角 5. 线线平行与垂直的判定与性质 6. 线面平行与垂直的判定与性质 7. 面面平行与垂直的判定与性质 8. 空间向量的坐标运算、数量积 9. 用空间向量证明平行与垂直 10. 用空间向量求空间角 热考题型一 　空间几何体的三视图及表面积与体积 【 考情分析 】 难度 : 中档题 题型 : 以选择题、填空题为主 考查方式 : 已知三视图 , 求几何体的表面积与体积或已知几何体判断三视图 【 考题集训 】 1.(2014· 重庆高考 ) 某几何体的三视图如图所示 , 则该几何体的表面积为　 ( 　　 ) A.54 B.60 C.66 D.72 【 解析 】 选 B. 由三视图可知该几何体为如图所示的一个三棱柱上方被截去一个三棱锥得到的 . 由三视图中的相关数据易知 , 表面积为 2.(2014· 辽宁高考 ) 某几何体的三视图如图所示 , 则该几何体的体积为　 ( 　　 ) A.8-2π B.8-π C.8- D.8- 【 解析 】 选 B. 由三视图可知该几何体为一个正方体截 去两个 圆柱 . 截得该几何体的原正方体的体积为 2×2×2=8; 截去的 圆柱 ( 部分 ) 底面半径为 1, 母线长为 2, 截去的两部分 体积为 (π×1 2 ×2)×2=π, 故该几何体的体积为 8-π. 3.(2014· 山东高考 ) 三棱锥 P-ABC 中 , 点 D,E 分别为 PB,PC 的中点 , 记三棱锥 D-ABE 的体积为 V 1 ,P-ABC 的体积 为 V 2 , 则 = 　　　　 . 【 解析 】 分别过点 E,C 向平面 PAB 作高 h 1 ,h 2 , 由 E 为 PC 的 中点得 = , 由 D 为 PB 的中点得 S △ABD = S △ABP , 所以 V 1 ∶V 2 = 答案 : 热考题型二 　多面体与球的“切”“接”问题 【 考情分析 】 难度 : 中档题 题型 : 选择题、填空题 考查方式 : 以锥体、柱体的外接球为载体 , 考查学生的空间想象力及运算能力 【 考题集训 】 1.(2014· 陕西高考 ) 已知底面边长为 1, 侧棱长为 的正四棱柱的各顶点均在同一个球面上 , 则该球的体 积 为　 ( 　　 ) A. B.4π C.2π D. 【 解析 】 选 D. 由正四棱柱的各顶点均在同一个球面上 , 可设正四棱柱的上底所在截面圆的半径为 R 1 , 则 + =1 可得 = ; 又侧棱长为 , 所以球心到截面圆的 距离 d= ; 由截面圆半径、球心距、球半径构成直角 三角形 , 根据勾股定理得球半径 R= 代入球的体积公式得球的体积为 . 2.(2016· 沈阳模拟 ) 已知一个正方体的所有顶点在一 个球面上 . 若球的体积为 , 则正方体的棱长 为 　　　　　 . 【 解析 】 设球半径为 R, 因为球的体积为 π R 3 = , 所 以 R= , 又由球的直径与其内接正方体对角线的相等 关系知正方体的对角线长为 3, 故其棱长为 . 答案 : 热考题型三 　直线、平面平行与垂直的判定与性质 【 考情分析 】 难度 : 中档题 题型 : 选择题、解答题 考查方式 : 借助空间几何体或直接考查线、面平行与垂直的判定与性质定理 【 考题集训 】 1.(2016· 合肥模拟 ) 设 m,n 是两条不同的直线 ,α,β 是 两个不同的平面　 ( 　　 ) A. 若 m∥α,n∥α , 则 m∥n B. 若 m∥α,m∥β , 则 α∥β C. 若 m∥n,m⊥α , 则 n⊥α D. 若 m∥α,α⊥β , 则 m⊥β 【 解析 】 选 C.A 选项中 m 与 n 还有可能相交或异面 ;B 选项中 α 与 β 还有可能相交 ;D 选项中 m 与 β 还有可能平行或 m ⊂ β . 2.(2015· 湖南高考 ) 如图 , 直三棱柱 ABC-A 1 B 1 C 1 的底面是边长为 2 的正三角形 , 点 E,F 分别是 BC,CC 1 的中点 . (1) 证明 : 平面 AEF⊥ 平面 B 1 BCC 1 . (2) 若直线 A 1 C 与平面 A 1 ABB 1 所成的角为 45°, 求三棱锥 F-AEC 的体积 . 【 解析 】 (1) 如图 , 因为三棱柱 ABC-A 1 B 1 C 1 是直三棱柱 , 所以 AE⊥BB 1 , 又点 E 是正三角形 ABC 的边 BC 的中点 , 所以 AE⊥BC, 因此 AE⊥ 平面 B 1 BCC 1 , 而 AE⊂ 平面 AEF, 所以平面 AEF⊥ 平面 B 1 BCC 1 . (2) 设 AB 的中点为 D, 连接 A 1 D,CD, 因为△ ABC 是正三角形 , 所以 CD⊥AB, 又三棱柱 ABC-A 1 B 1 C 1 是直三棱柱 , 所以 CD⊥AA 1 , 因此 CD⊥ 平面 A 1 ABB 1 , 于是∠ CA 1 D 为直线 A 1 C 与平面 A 1 ABB 1 所成的角 , 由题设知 ∠ CA 1 D=45°, 所以 A 1 D=CD= AB= , 在 Rt△AA 1 D 中 ,AA 1 = 所以 FC= AA 1 = , 故三棱锥 F-AEC 的体积 V= S △AEC ×FC= × × = . 3.(2015· 湖北高考 )《 九章算术 》 中 , 将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马 , 将四个面都为直角三角形的四面体称之为鳖臑 . 如图 , 在阳马 P-ABCD 中 , 侧棱 PD⊥ 底面 ABCD, 且 PD=CD, 点 E 是 PC 的中点 , 连接 DE,BD,BE. (1) 证明 :DE⊥ 平面 PBC. 试判断四面体 EBCD 是否为鳖臑 , 若是 , 写出其每个面的直角 ( 只需写出结论 ); 若不是 , 请 说明理由 . (2) 记阳马 P-ABCD 的体积为 V 1 , 四面体 EBCD 的体积为 V 2 , 求 的值 . 【 解析 】 (1) 因为 PD ⊥ 底面 ABCD, 所以 PD ⊥ BC. 由底面 ABCD 为长方形 , 有 BC⊥CD, 而 PD∩CD=D, 所以 BC⊥ 平面 PCD. DE⊂ 平面 PCD, 所以 BC⊥DE. 又因为 PD=CD, 点 E 是 PC 的中点 , 所以 DE⊥PC. 而 PC∩BC=C, 所以 DE⊥ 平面 PBC. 由 BC⊥ 平面 PCD,DE⊥ 平面 PBC, 可知四面体 EBCD 的四个面都是直角三角形 , 即四面体 EBCD 是一个鳖臑 , 其四个面的直角分别是∠ BCD,∠BCE,∠DEC,∠DEB. (2) 由已知 ,PD 是阳马 P-ABCD 的高 , 所以 V 1 = S ABCD · PD= BC · CD · PD; 由 (1) 知 ,DE 是鳖臑 D-BCE 的高 ,BC⊥CE, 所以 V 2 = S △BCE · DE= BC · CE · DE. 在 Rt△PDC 中 , 因为 PD=CD, 点 E 是 PC 的中点 , 所以 DE=CE= CD, 于是 热考题型四 　空间向量及其应用 【 考情分析 】 难度 : 中档题 题型 : 解答题 考查方式 : 以空间几何体为背景 , 考查用空间向量求空间角 【 考题集训 】 1.(2015· 重庆高考 ) 如图 , 三棱锥 P-ABC 中 ,PC⊥ 平面 ABC,PC=3,∠ACB= . 点 D,E 分别为线段 AB,BC 上的点 , 且 CD=DE= ,CE=2EB=2. (1) 证明 :DE⊥ 平面 PCD. (2) 求二面角 A-PD-C 的余弦值 . 【 解析 】 (1) 由 PC ⊥ 平面 ABC,DE ⊂ 平面 ABC, 故 PC⊥DE. 由 CE=2,CD=DE= 得△ CDE 为等腰直角三角形 , 故 CD⊥DE. 由 PC∩CD=C,DE 垂直于平面 PCD 内两条相交直线 , 故 DE⊥ 平面 PCD. (2) 由 (1) 可知 ,△CDE 为等腰直角三角形 ,∠DCE= , 如 图 , 过点 D 作 DF⊥CE 于点 F, 易知 DF=FC=FE=1, 又已知 EB=1, 故 FB=2. 由∠ ACB= , 得 DF∥AC, , 故 AC= DF= . 以 C 为坐标原点 , 分别以 , 的方向为 x 轴 ,y 轴 ,z 轴的正方向建立空间直角坐标系 , 则 C(0,0,0),P(0,0,3),A( ),E(0,2,0),D(1,1,0), 设平面 PAD 的法向量为 n 1 =(x 1 ,y 1 ,z 1 ), 由 (1) 可知 DE⊥ 平面 PCD, 故平面 PCD 的法向量 n 2 可取 为 , 即 n 2 =(1,-1,0), 从而法向量 n 1 , n 2 的夹角的余弦值为 cos < n 1 , n 2 >= = , 故所求二面角 A-PD-C 的余弦值为 . 2.(2015· 北京高考 ) 如图 , 在四棱锥 A-EFCB 中 ,△AEF 为等边三角形 , 平面 AEF⊥ 平面 EFCB,EF∥BC,BC=4,EF=2a, ∠EBC=∠FCB=60°,O 为 EF 的中点 . (1) 求证 :AO⊥BE. (2) 求二面角 F-AE-B 的余弦值 . (3) 若 BE⊥ 平面 AOC, 求 a 的值 . 【 解析 】 (1) 因为△ AEF 是等边三角形 ,O 为 EF 的中点 , 所 以 AO ⊥ EF. 又因为平面 AEF⊥ 平面 EFCB, 平面 AEF∩ 平面 EFCB=EF, AO⊂ 平面 AEF, 所以 AO⊥ 平面 EBCF. 因为 BE⊂ 平面 EBCF, 所以 AO⊥BE. (2) 取 BC 的中点 D, 连接 OD. 由已知四边形 BEFC 为等腰梯形 , 且 O,D 分别为两底的中点 , 所以 OD⊥EF, 如图 , 分别以 OE,OD,OA 为 x,y,z 轴建立空间直角坐标系 , 则 A(0,0, a), E(a,0,0),B(2,2 - a,0), 设平面 ABE 的法向量 n 1 =(x,y,z ), 则 平面 AEF 的一个法向量为 n 2 =(0,1,0). 所以 cos < n 1 , n 2 >= 因为二面角 F-AE-B 为钝二面角 , 所以余弦值为 - . (3) 由 (1) 知 AO⊥ 平面 EFCB. 因为 BE⊂ 平面 EFCB, 所以 AO⊥EB. 要使 BE⊥ 平面 AOC, 只需 BE⊥OC. 因为 =(2-a,2 - a,0), =(-2,2 - a,0), 所以 · =-4+2a+(2 - a) 2 =0, 即 3a 2 -10a+8=0 , 解得 a=2( 舍 ) 或 a= .