数学卷·2018届山东省实验中学高三上学期第二次诊断考试数学（理）试题（解析版） 15页

山东省实验中学 2015 级高三第二次诊断性考试 数学试题（理科） 2017.11 说明：本试卷满分 150 分，分为第 I 卷（选择题）和第 II 卷（非选择题）两 部分，第 I 卷为第 1 页至第 3 页，第 II 卷为第 3 页至第 6 页.试题答案请用 2B 铅笔或 0.5mm 签字笔填涂到答题卡规定位置上，书写在试题上的答案无效. 考试时间 120 分钟. 第 I 卷（共 60 分） 一、选择题（本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个 选项中，只有一项是符合题目要求的） 1. 已知全集为 R，集合 A= ,B= ,则 A B=( ) A. B. C. D. 【答案】C 【解析】A= ,B= ,则 A B= ,故选 C 点晴:集合的三要素是：确定性、互异性和无序性.研究一个集合，我们首先要看清楚它的 研究对象，是实数还是点的坐标还是其它的一些元素，这是很关键的一步.第二步常常是解 一元二次不等式，我们首先用十字相乘法分解因式，求得不等式的解集.在解分式不等式的 过程中，要注意分母不能为零.元素与集合之间是属于和不属于的关系，集合与集合间有包 含关系. 在求交集时注意区间端点的取舍. 熟练画数轴来解交集、并集和补集的题目 2. 已知 ，命题“若 则 ”的否命题是( ) A. 若 则 B. 若 则 C. 若 则 D. 若 则 【答案】A 【解析】试题分析：原命题为若 则 ，那么否命题就是若 则 ，所以否命题是若 ，则 ，故选 A. 考点：四种命题 3. 已知函数 ，则 的值为( ) A. 4 B. C. 3 D. 【答案】B 【解析】由已知 ,故选 B 4. 空气质量指数（Air Quality Index，简称 AQI）是定量描述空气质量状况的无量纲指数， 空气质量按照 AQI 大小分为六级：0~50 为优，51~100 为良。101~150 为轻度污染， 151~200 为中度污染，201~250 为重度污染，251~300 为严重污染。一环保人士记录去年某 地某月 10 天的 AQI 的茎叶图。利用该样本估计该地本月空气质量状况优良（AQI≤100） 的天数( )（这个月按 30 计算） A. 15 B. 18 C. 20 D. 24 【答案】B 【解析】从茎叶图中可以发现这样本中空气质量优的天数为 2, 空气质量良的天数为 4, 该样本中空气质量优良的频率为 , 从而估计该月空气质量优良的天数为 5. 曲线若 和直线 围成的图形面积为( ) A. B. C. D. 【答案】D 【解析】试题分析：令 ，所以面积为 . 6. 已知函数 ，则 是( ) A. 奇函数，且在 上单调递增 B. 偶函数，且 在上单调递增 C. 奇函数，且在 上单调递减 D. 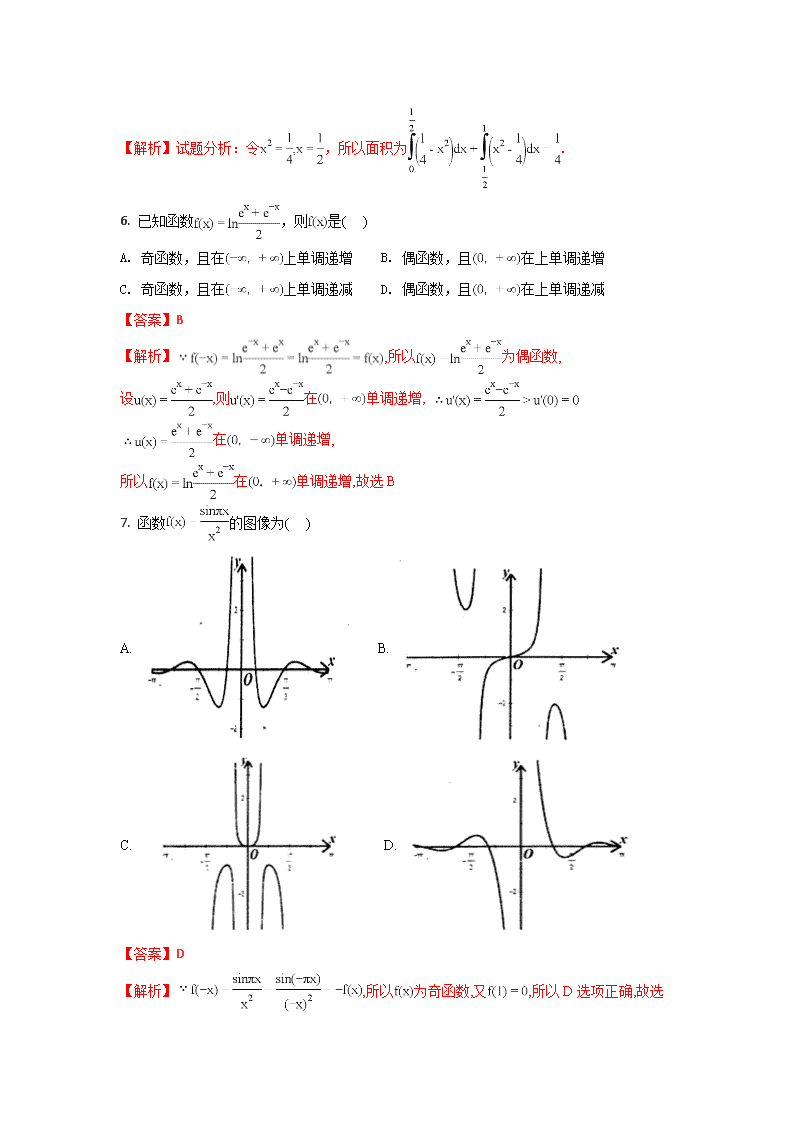偶函数，且 在上单调递减 【答案】B 【解析】 ,所以 为偶函数, 设 ,则 在 单调递增, 在 单调递增, 所以 在 单调递增,故选 B 7. 函数 的图像为( ) A. B. C. D. 【答案】D 【解析】 ,所以 为奇函数,又 ,所以 D 选项正确,故选 D 8. 奇函数 定义域为 R，当 时， ，且函数 为偶函数，则 的值为( ) A. B. 2 C. D. 3 【答案】A 【解析】 为 R 上的奇函数, 为偶函数, ; 是周期为 4 的周期函数; ;故选 A 点睛：抽象函数的周期性：（1）若 ，则函数 周期为 T； （2）若 ，则 函数周期为|a-b| （3）若 ，则函数的周期为 2a； （4）若 ，则函数的周期为 2a. 9. 曲线 上的点到直线 的最短距离是( ) A. B. C. D. 0 【答案】C 【解析】试题分析：直线 的斜率为２。由于 ，则由 得 ，则 ，求得曲线 上斜率为２的切线为 。取 上的点 ，则点Ａ到直线 的距离为 ，所以所求的最短距离为 。故选 Ｃ。 考点：点到直线的距离公式 点评：在解决问题时，有些问题需要进行转化。像本题，需将要求的问题转化为两条直线 之间的距离。 10. 已知命题：命题 ；命题 ，且 是 的充分不必要条件，则的取值范围 ( ) A. B. C. D. 【答案】A 【解析】命题 即 , 是 的充分不必要条件,所以是的充分不必要条 件, , ,故选 A. 11. 某中学学生会为了调查爱好游泳运动与性别是否有关，通过随机询问 110 名性别不同 的高中生是否爱好游泳运动得到如下的列联表： 由 并参照附表，得到的正确结论是( ) A. 在犯错误的概率不超过 1%的前提下，认为“爱好游泳运动与性别有关” B. 在犯错误的概率不超过 1%的前提下，认为“爱好游泳运动与性别无关” C. 有 99.9%的把握认为“爱好游泳运动与性别有关” D. 有 99.9%的把握认为“爱好游泳运动与性别无关” 【答案】A 【解析】 ,所以有 99%的把握认为“爱好游泳运动与 性别有关”,所以在犯错误的概率不超过 1%的前提下，认为“爱好游泳运动与性别有关” 12. .已知 是定义在 上的函数， 是它的导函数，且恒有 成立，则( ) A. B. C. D. 【答案】D 【解析】构造函数 ，根据已知则 在 上单调递增， 即 ， 即 故选 D. 点睛：本题主要考查利用导数研究函数的单调性，需要构造函数，一般：（1）条件含有 ，就构造 ,（2）若 ，就构造 ，便于给出导数时联想 构造函数.本题中可以构造 ，则有 第 II 卷（非选择题，共 90 分） 二、填空题（本题共 4 小题，每小题 5 分，共 20 分） 13. 函数 的定义域是_______________ 【答案】 【解析】由题要使函数有意义须满足 14. 如果方程 的两个实根一个小于 1，另一个大于 1，那么实数 m 的 取值范围是____________. 【答案】 【解析】设方程 对应的二次函数 ,开口向上, 方程 的两个实根一个小于 1，另一个大于 1， 可得 ,即 15. 若函数 函数 的零点个数是________. 【答案】4 【解析】由 =0 得 ， 设 ，则等价为 ， 当 时，由 得 ， 当 时，由 得 ， 即 或 ， 当 时，由 得 ，由 ，得 ，故此 时有两个零点， 当 时，由 得 ，由 ，得 ，故此时有两 个零点 综上函数 的零点个数是 4，故答案为：4. 点睛：本题考查的是函数零点的个数问题.函数零点问题的处理一般有以下几种方法：1、 通过解方程得到函数的零点，得到零点个数；2、利用二分法判断函数的零点，3、利用函 数与方程思想，通过分离化原函数为两个函数，转化为利用两个函数图象的交点个数来判 断函数的零点个数. 16. 对于函数 ，若存在常数 ，使得取 定义域内的每一个值，都有 ， 则称为准奇函数，给出下列函数 ① ，② ，③ ，④ ，⑤ ， ⑥ ，其中所有准奇函数的序号是_________________。 【答案】②④⑤⑥ 【解析】对于函数 ，若存在常数 ，使得取 定义域内的每一个值，都有 知， 函数 f(x)的图象关于(a,0)对称， 对于① ，函数无对称中心， 对于② ,函数 f(x)的图象关于(-1,0)对称， 对于③ ,函数 f(x)关于(0,0)对称， 对于④ ,函数 f(x)的图象关于 对称， 对于⑤ ,函数 f(x)的图象关于 对称， 对于⑥ ，由奇函数 向右平移一个单位得到，函数 f(x)的图象关 于 对称， 故答案为②④⑤⑥ 三、解答题（共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17-21 为必考题，每个试题考生都必须作答.第 22、23 题为选考题，考生根据要求作 答.） （一）必考题：60 分. 17. 根据《中华人民共和国道路交通安全法》规定：“车辆驾驶员血液酒精溶度（单位 mg/100ml）/在 ，属于酒后驾驶；血液浓度不低于 80，属于醉酒驾驶。”2017 年 “中秋节”晚 9 点开始，济南市交警队在杆石桥交通岗前设点，对过往的车辆进行检查， 经过 4 个小时，共查处喝过酒的驾驶者 60 名，下图是用酒精测试仪对这 60 名驾驶者血液 中酒精溶度进行检测后所得结果画出的频率分布直方图。 （1）求这 60 名驾驶者中属于醉酒驾车的人数（图中每组包括左端点，不包括右端点） （2）若以各小组的中值为该组的估计值，频率为概率的估计值，求这 60 名驾驶者血液的 酒精浓度的平均值。 【答案】(1)3(人)（2）47 【解析】试题分析：(1)根据频率= ,计算所求的频数即可; (2)利用频率分布直方图求出数据的平均值即可; 试题解析：(1)由频率分布直方图可知： 醉酒驾驶的频率为 所以醉酒驾驶的人数为 (人) （2）由频率分布直方图可知 酒精浓度 25 35 45 55 65 75 85 频率 0.25 0.15 0.2 0.15 0.1 0.1 0.05 所以 =47 18. 已知函数 . （1）若曲线 在点 处的切线的倾斜角为，求实数 a 的值. （2）若函数 在区间 上单调递增，求实数 a 的范围. 【答案】（1） （2） 【解析】试题分析：（1）根据切线的倾斜角为得到切线的斜率,根据导数的几何意义可以 知道 处的导数即为切线的斜率,建立等量关系,求出 a 即可; （2）根据函数 在区间 上单调递增,可转化成 ,对 恒成立, 将参数 a 分离,转化成当 时,不等式 恒成立,利用均值不等式求出不等式 右边函数的最小值，进而得实数 a 的范围 试题解析： （1） 则可得： .- （2）由函数 在区间 上单调递增 则 对一切的 恒成立. 即 恒成立， 令 函数 在 上单调递减，当 时， 所以的取值范围是 . 19. 某企业为了对新研发的一批产品进行合理定价，将产品按事先拟定的价格进行试销， 得到一组销售数据 ，如表所示： 已知 （1）求的值 （2）已知变量 具有线性相关性，求产品销量关于试销单价的线性回归方程 可 供选择的数据 （3）用表示（2）中所求的线性回归方程得到的与 对应的产品销量的估计值。当销售数 据 对应的残差的绝对值 时，则将销售数据 称为一个“好数 据”。试求这6 组销售数据中的 “好数据”。 参考数据：线性回归方程中 的最小二乘估计分别是 【答案】（1） （2） （3） 【解析】试题分析：(Ⅰ)由 = ,可求出 q 的值; (Ⅱ)求出回归系数,可得线性回归方程 ; (Ⅲ)分别求出 检验是否满足 ，从而判断是否为“好数据”。 试题解析： （1） 又 ， （2） ， （3） ，所以 是好数据； ，所以 不是好数据 ，所以 是好数据 ，所以 不是好数据 所以 是好数据 所以 不是好数据 所以好数据为 20. 已知函数 . （1）求函数 的单调区间； （2）设 当 ，不等式 恒成立，求 k 的最大值. 【答案】(1) 当 时，在 上， 单调递增.当 时，在 上， 单调递减； 在 上， 单调递增. （2）4 【解析】试题分析：(1)先求函数的导数,利用导数确定函数的单调区间. (2)分离常数得到 构造函数 ,利用导数 求函数 的最值,然后得 k 的范围.最终确定 k 的最大值. 试题解析： (1)函数 定义域为 ， ， 当 时，在 上， 单调递增；- 当 时，在 上， 单调递减；在 上， 单调递增； 综上所述：当 时，在 上， 单调递增. 当 时，在 上， 单调递减；在 上， 单调递增. （2） 等价于 令 ， 令 ，易知 在 上单调递增.- ， 所以存在 , 使得 .即 .- 在 上, , 单调递减,在 上, , 单调递增. 所以 . 求的最大值为 4. 21. 已知函数 . （1）若 ，求函数 的极值； （2）若函数 有两个零点，求实数 a 的取值范围. 【答案】（1） 时， 取极大值 ，当 时， 取极小值 .（2） 【解析】试题分析：(1)求出 的导数,判断单调区间,可得极值; (2)根据题意可得 ，分 ， 和 三种情 况，讨论函数的增减情况，判断函数的零点个数. 试题解析： （1）函数定义域为 ， . 解得 ---1 分 列表： + 0 _ 0 + 极大值 极小值 所以 时， 取极大值 ，当 时， 取极小值 . （2） 当 时，易知函数 f(x)只有一个零点，不符合题意； 当 时，在 上， 单调递减； 在 上， 单调递增； ，且 所以函数 有两个零点. 当 时，在 和 上 单调递增；在 和 上 单调递减； ，函数 至多有一个零点，不符合题意. 当 时，在 和 上 单调递增；在 上 单调递 减； ，函数 至多有一个零点，不符合题意. 综上：实数 a 的取值范围是 . 点睛:导数是研究函数的单调性、极值(最值)最有效的工具对导数的应用的考查主要从以下 几个角度进行：（1）考查导数的几何意义，往往与解析几何、微积分相联系；（2）利用 导数求函数的单调区间，判断单调性；已知单调性求参数；（3）利用导数求函数的最值 (极值)，解决生活中的优化问题；（4）考查数形结合思想的应用． (二)选考题：共 10 分.请考生在第 22、23 题中任选一题作答，则按所做的第 一题计分. 22. [选修 4-4，坐标系与参数方程] 在平面直角坐标系 中，曲线 C 的参数方程为 ，以坐标原点为极 点，以轴正半轴为极轴建立极坐标系，直线的极坐标方程为 。 （1）求直线的直角坐标方程和曲线 C 的普通方程。 （2）设点 P 为曲线 C 上的任意一点，求点 P 到直线的距离的最大值。 【答案】⑴ , ⑵ 【解析】试题分析：(Ⅰ)直线 l 的极坐标方程可化为 ,由此可得直线 l 的直角坐标方程.曲线 C 的参数方程消去参数 ,能求出曲线 C 的普通方程. (Ⅱ)设点 为曲线 C 上任意一点,利用点到直线的距离公式及三角函数性质能 求出点 P 到直线 l 的距离的最大值. 试题解析： ⑴因为直线的极坐标方程为 ， 所以 ，即 曲线 的参数方程为 （ 为参数） 所以 ⑵设 ，则 到直线的距离为 所以当 时，取最大值 23. [选修 4—5：不等式选讲] 设函数 （1）解不等式 （2）对任意的实数 ，若 求证： 【答案】⑴ （2）见解析 【解析】试题分析：(1)分段讨论，去掉绝对值符号求解不等式即可； (2)利用绝对值三角不等式的性质证明即可，注意等号成立的条件. 试题解析： ⑴①当 时，原不等式可化为 ，可得 ，所以 当 时，原不等式可化为 ，恒成立，所以 当 时，原不等式可化为 ，可得 ，所以 综上，不等式的解集为 （2）证明： 点睛】: 的解法一般有两种方法： ①零点分段讨论法：利用绝对值的分界点将区间进行分段，进而去掉绝对值符号，将问题 转化成分段不等式组进行求解； ②绝对值的几何意义：对于 的类型，可以利用绝对值的几何意义进行 求解．