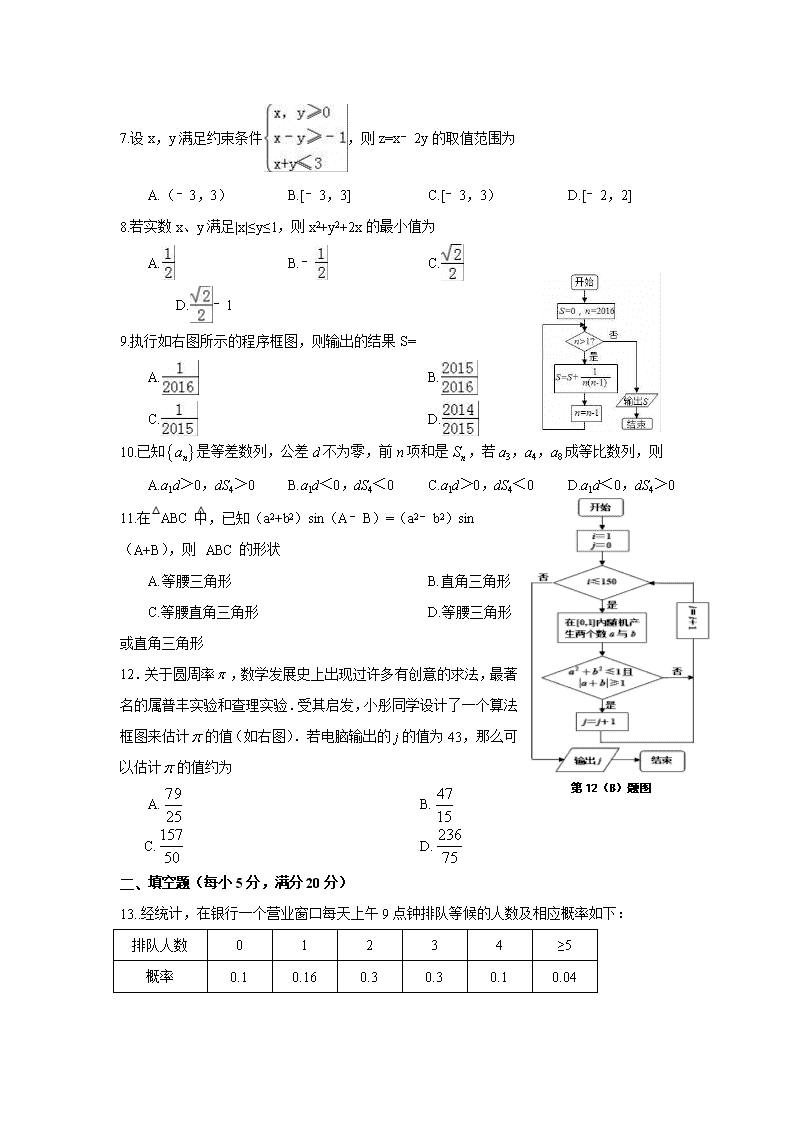
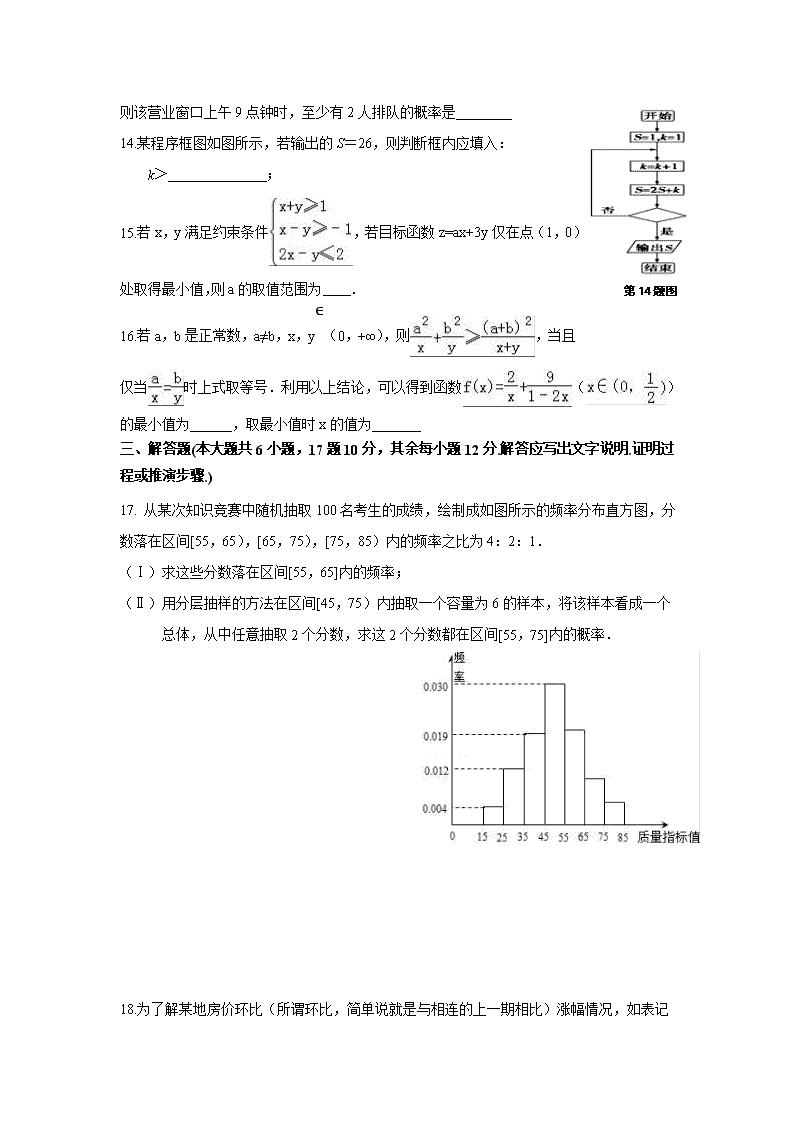
- 297.50 KB
- 2021-06-30 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
考试时间:2017年10月12—13日
上饶县中学2019届高二年级上学期第一次月考
数 学 试 卷(理零)
命题人:苏笃春 审题人:严 俊 时间:120分钟 总分:150分
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某校期末考试后,为了分析该校高一年级1000名学生的学习成绩,从中随机抽取了100名学生的成绩单,就这个问题来说,下面说法正确的是
A.1000名学生是总体 B.每个学生是个体
C.100名学生的成绩是一个个体 D.样本的容量是100
2.已知等差数列中,a2+a4=6,则a1+a2+a3+a4+a5 =
A.30 B.15 C. D.
x=0
Do
x=x+1
x=x^2
Loop While x<20
输出 x
第4题图
3.从区间[﹣1,1]内随机取出一个数a,使3a+1>0的概率为
A. B.
C. D.
4.如右图,程序的循环次数为
A.1 B.2
C.3 D.4
5.在△ABC中,若a2﹣b2=bc,sinC=2sinB,则A=
A.30° B.60° C.120° D.150°
第6题图
6.如图是从甲、乙两品种的棉花中各抽测了10根棉花的纤维长度(单位:mm)所得数据如图茎叶图,记甲、乙两品种棉花的纤维长度的平均值分别为与,标准差分别为与,则下列说法不正确的是
A.
B.
C.乙棉花的中位数为325.5mm
D.甲棉花的众数为322mm
7.设x,y满足约束条件,则z=x﹣2y的取值范围为
A.(﹣3,3) B.[﹣3,3] C.[﹣3,3) D.[﹣2,2]
8.若实数x、y满足|x|≤y≤1,则x2+y2+2x的最小值为
A. B.﹣ C. D.﹣1
9.执行如右图所示的程序框图,则输出的结果S=
A. B.
C. D.
10.已知是等差数列,公差d不为零,前n项和是,若a3,a4,a8成等比数列,则
第12(B)题图
A.a1d>0,dS4>0 B.a1d<0,dS4<0 C.a1d>0,dS4<0 D.a1d<0,dS4>0
11.在△ABC中,已知(a2+b2)sin(A﹣B)=(a2﹣b2)sin(A+B),则△ABC的形状
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
12.关于圆周率,数学发展史上出现过许多有创意的求法,最著名的属普丰实验和查理实验.受其启发,小彤同学设计了一个算法框图来估计的值(如右图).若电脑输出的j的值为43,那么可以估计的值约为
A. B.
C. D.
二、 填空题(每小5分,满分20分)
13..经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:
排队人数
0
1
2
3
4
≥5
概率
0.1
0.16
0.3
0.3
0.1
0.04
第14题图
则该营业窗口上午9点钟时,至少有2人排队的概率是
14.某程序框图如图所示,若输出的S=26,则判断框内应填入:
k> ;
15. 若x,y满足约束条件,若目标函数z=ax+3y仅在点(1,0)处取得最小值,则a的取值范围为 .
16.若a,b是正常数,a≠b,x,y∈(0,+∞),则,当且仅当时上式取等号.利用以上结论,可以得到函数()的最小值为 ,取最小值时x的值为
三、解答题(本大题共6小题,17题10分,其余每小题12分.解答应写出文字说明.证明过程或推演步骤.)
17. 从某次知识竞赛中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85)内的频率之比为4:2:1.
(Ⅰ)求这些分数落在区间[55,65]内的频率;
(Ⅱ)用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,将该样本看成一个总体,从中任意抽取2个分数,求这2个分数都在区间[55,75]内的概率.
18.为了解某地房价环比(所谓环比,简单说就是与相连的上一期相比)涨幅情况,如表记录了某年1月到5月的月份x(单位:月)与当月上涨的百比率y之间的关系:
时间x
1
2
3
4
5
上涨率y
0.1
0.2
0.3
0.3
0.1
(1)根据如表提供的数据,求y关于x的线性回归方程y=x+;
(2)预测该地6月份上涨的百分率是多少?
(参考公式:用最小二乘法求线性回归方程系数公式=, =﹣)
19.在△ABC中,A、B、C的对边分别为a,b,c,已知A≠,且3sinAcosB+bsin2A=3sinC.
(I)求a的值;
(Ⅱ)若A=,求△ABC周长的最大值.
20.(1)设函数f(x)=,求不等式f(x)≤1的解集
(2) 已知a>b>c且恒成立,求实数m的最大值.
21.已知袋子中装有红色球1个,黄色球1个,黑色球n个(小球大小形状相同),从中随机抽取1个小球,取到黑色小球的概率是.
(Ⅰ)求n的值;
(Ⅱ)若红色球标号为0,黄色球标号为1,黑色球标号为2,现从袋子中有放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
(ⅰ)记“a+b=2”为事件A,求事件A的概率;
(ⅱ)在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a﹣b)2恒成立”的概率.
22.已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线x﹣y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项an和bn;
(2)求证:;
(3)设cn=an•bn,求数列{cn}的前n项和Tn.
理零答案
1.D 2.B 3.C 4.C 5.A 6. D 7.B
8.B 9.B 10.B 11.D 12.D
二、填空题
13..0.74 14.k>3 15.(﹣6,3) 16.25,
三、解答题
17.解:(Ⅰ)设区间[75,85)内的频率为x,
则区间[55,65),[65,75)内的频率分别为4x和2x.…
依题意得(0.004+0.012+0.019+0.030)×10+4x+2x+x=1,…
解得x=0.05.所以区间[55,65]内的频率为0.2.…
(Ⅱ)由(Ⅰ)得,区间[45,55),[55,65),[65,75)内的频率依次为0.3,0.2,0.1.
用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,
则在区间[45,55)内应抽取件,记为A1,A2,A3.
在区间[55,65)内应抽取件,记为B1,B2.
在区间[65,75)内应抽取件,记为C.…
设“从样本中任意抽取2件产品,这2件产品都在区间[55,75]内”为事件M,
则所有的基本事件有:{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A1,C},{A2,A3},{A2,B1},{A2,B2},{A2,C},{A3,B1},{A3,B2},{A3,C},{B1,B2},{B1,C},{B2,C},共15种.…
事件M包含的基本事件有:{B1,B2},{B1,C},{B2,C},共3种.…
所以这2件产品都在区间[55,75]内的概率为.…
18.解:(1)由题意, =3, =0.2…
12+22+32+42+52=55,…
1×0.1+2×0.2+3×0.3+4×0.3+5×0.1=3.1…
所以…
…
∴回归直线方程为y=0.01x+0.17…
(2)当x=6时,y=0.01×6+0.17=0.23…
预测该地6月份上涨的百分率是0.23…
19.解:(I)∵3sinAcosB+bsin2A=3sinC,
∴3sinAcosB+bsin2A=3sinAcosB+3cosAsinB,
∴bsinAcosA=3cosAsinB,
∴ba=3b,
∴a=3;
(Ⅱ)由正弦定理可得==,
∴b=2sinB,c=2sinC
∴△ABC周长=3+2(sinB+sinC)=3+2 [sin(﹣C)+sinC]=3+2sin(+C)
∵0<C<,
∴<+C<,
∴<sin(+C)≤1,
∴△ABC周长的最大值为3+2.
20.解:(1)若log4x≤1,解得:x≤4,故x∈[1,4],
若2﹣x≤1,解得:x≥0,故x∈[0,1),
综上,不等式的解集是[0,4].
(2)由题意,a﹣b>0,b﹣c>0,a﹣c>0,
∴转化为:.
可得:.
分离: 3+2.(当且仅当(a﹣b)=(b﹣c)时取等号)
∴实数m的最大值为3.
21.解:(Ⅰ)依题意,得n=1
(Ⅱ)(ⅰ)记标号为0的小球为s,标号为1的小球为t,标号为2的小球为k,
则取出2个小球的可能情况有:(s,t),(s,k),(t,s),(t,k),(k,s),(k,t),(s,s),(t,t),(k,k),共9种,
其中满足“a+b=2”的有3种:(s,k),(k,s)(t,t).
所以所求概率为
(ⅱ)记“x2+y2>(a﹣b)2恒成立”为事件B.
则事件B等价于“x2+y2>4恒成立”,(x,y)可以看成平面中的点的坐标,则全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域为B={(x,y)|x2+y2>4,(x,y)∈Ω}.
所以所求的概率为P(B)==1﹣.
22.解:(1)∵an是Sn与2的等差中项,∴Sn=2an﹣2,
∴Sn﹣1=2an﹣1﹣2,∴an=Sn﹣Sn﹣1=2an﹣2an﹣1,
又a1=2,∴an≠0,(n≥2,n∈N*),
即数列{an}是等比数列,,
∵点P(bn,bn+1)在直线x﹣y+2=0上,∴bn﹣bn+1+2=0,bn+1﹣bn=2,
即数列{bn}是等差数列,又b1=1,∴bn=2n﹣1.
(2)∵,
∴==.
(3)∵,
∴Tn=a1b1+a2b2+…+anbn=1×2+3×22+5×23+…+(2n﹣1)2n,
∴,
因此,,
即,
∴.