- 597.00 KB
- 2021-06-30 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
平行线分线段成比例定理(
2
)
学习目标
:
1
、
会
识别平行线分线段成比例的变式图形。
2
、
能
写出图中的成比例线段。
3
、
理解
平行线分线段成比例定理的推论。
4
、
会
用推论去计算和证明有关的问题。
5
、
建立
一种解题模型。
6
、
会
用
“
运动
”
的观点去研究解决问题。
7
、
欣赏
数学的美学文化
——
理性美、结构美。
引导材料
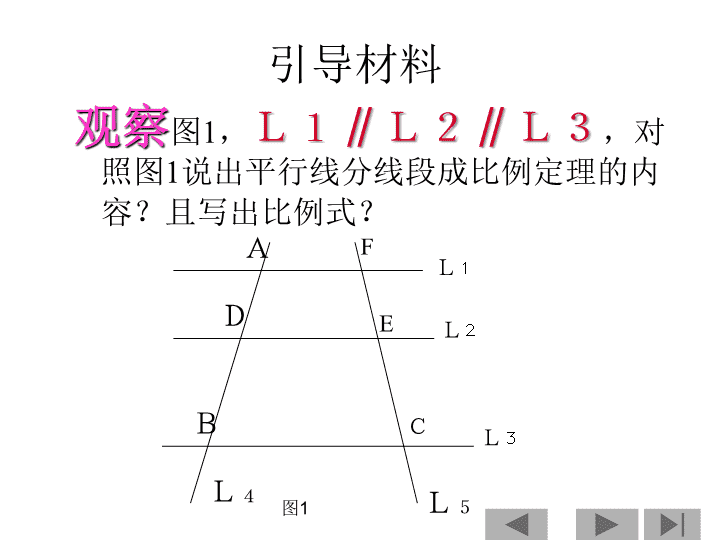
观察
图
1
,
L1∥L2∥L3
,对照
图
1
说
出平行线分线段成比例定理的内容?且写出比例式?
图
1
A
D
B
F
E
C
L
1
L
2
L
3
L
5
L
4
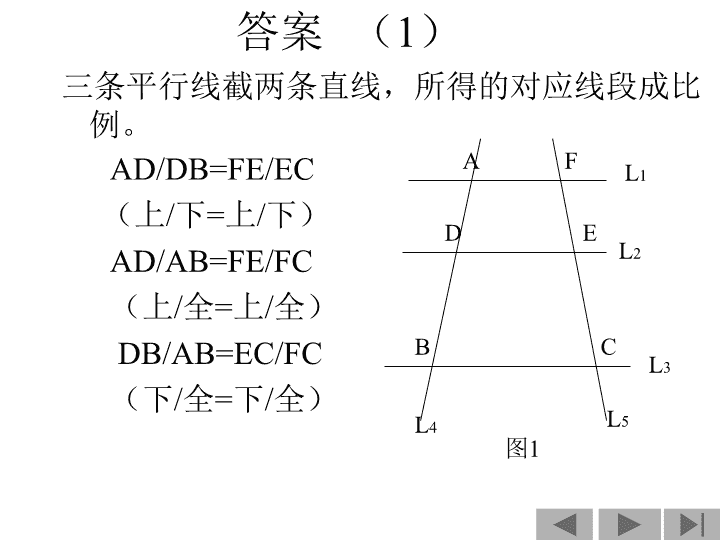
答案 (
1
)
三条平行线截两条直线,所得的对应线段成比例。
AD/DB=FE/EC
(上
/
下
=
上
/
下)
AD/AB=FE/FC
(上
/
全
=
上
/
全)
DB/AB=EC/FC
(下
/
全
=
下
/
全)
A
D
B
F
E
C
L
1
L
2
L
3
L
4
L
5
图
1
答案(
2
)
DB/AD=EC/FE
(下
/
上
=
下
/
上)
AB/AD=FC/FE
(
全
/
上
=
全
/
上
)
AB/DB=FC/EC
(
全
/
下
=
全
/
下
)
A
D
B
F
E
C
L
1
L
2
L
3
L
4
L
5
图
1
教学设计(
1
)
1
.
观察
图
2
、图
3
,说出它们分别是由图
1
怎样变化得到的?且写出图
2
、图
3
中有关的比例式?
A
D
B
F
E
C
A
D
B
E
C
L
1
L
2
L
3
L
1
L
2
L
3
图
1
图
2
(
)
怎样变化?
一般到 特殊
平行移动直线
FC
与直线
AB
相交,交点
A
在
L
1
上。
(F)
教学设计(
1
)续
续观察
A
D
B
F
E
C
L
1
L
2
L
3
图
1
(
)
F
A
D
B
C
L
1
L
2
L
3
图
3
怎样变化?
一般到特殊
平行移动直线
FC
与直线
AB
相交
,
交点
D
在
L
2
上
(E)
教学设计(
2
)
思考:
把图
2
、图
3
中的部分线擦去,得到图
4
、图
5
,上述比例式还成立吗?
A
D
B
E
L
1
L
2
L
3
C
部分线擦去
,
取一部分
A
D
B
E
C
(
)
字母 型
A
比例式
,
因为
图
2
图
4
一般到特殊
成立
图形中有关的对应线段均没改变
教学设计(
2
)续
续思考
F
A
D
B
C
(
E
)
图
3
部分线擦去
,
取一部分
F
A
D
(
E
)
B
C
图
5
(字母 型)
比例式
,
因为
一般到特殊
成立
图形中有关的对应线段均没改变
X
教学设计(
3
)
猜想:
⑴在图
4
、图
5
中,原题的条件(三条平行线)发生了什么变化?⑵结论有没有变?⑶
猜一猜,你能发现什么规律
?
A
D
B
E
C
A
D
B
E
C
图
2
图
4
F
A
D
B
C
(
E
)
F
A
D
(
E
)
B
C
图
3
图
5
部分线擦去
,
取一部分
一般到特殊
部分线擦去
,
取一部分
一般到特殊
(
1
)三条平行线剩下两条,且变为三角形的一边和截三角形另两边或两边延长线的线段。其中图
4
中
DE∥BC
,图
5
中
AF∥BC
(
2
)结论没变,所得的对应线段成比例。
(
3
)推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
例题解析
已知:
DE∥BC
,
AB
=
15
,
BD
=
4
,
AC
=
9
, 求:
AE
的长?
证明:∵
DE∥BC
∴AB/BD=AC/CE
(
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。)
即
15/4=9/CE
∴CE=12/5
∴AE=AC+CE
=9+12/5
=11.4
A
B
D
C
E
图
6
课堂练习(
1
)及答案
已知:
DE∥BC
,
AB
=
14
,
AC
=
18
,
AE
=
10
求:
AD
的长?
解:∵
DE∥BC
∴AD/AB=AE/AC
(
平行于三角形一边的直线截其他两边,所得的对应线段成比例。)
即
AD/14=10/18
∴AD=70/9
A
D
B
E
C
图
7
课堂练习(
2
)及答案
已知:
ED∥BC
,
AB
=
5
,
AC
=
7
,
AD
=
2
求:
AE
的长?
解:∵
ED∥BC
∴
AD/AB=AE/AC
(
平行于三角形一边的直线截其它两边的延长
线,所得的对应线段成比例)
即
2/5=AE/7
∴AE=14/5
E
D
A
B
C
图
8
5
7
2
课堂练习(
3
)及答案
已知:
AB⊥BD
,
ED⊥BD
,垂足分别为
B
、
D
求证:
AC
/
EC
=
BC
/
DC
证明:∵
AB⊥BD
,
ED⊥BD
∴∠B=∠D=90°
∴AB∥DE
∴AC/EC=BC/DC
(
平行于三角形一边的直线截其它两边的延长线,
所得的对应线段成比例)
A
B
C
D
E
┓
└
图
9
知识目标小结
1.
定理名称
:
2.
文字语言
:
3.
图形语言
:
4.
符号语言
:
5.
模型语言
:
A
D
E
B
C
F
A
D
B
C
字母 型 字母 型
图
4
图
5
平行线分线段成比例定理的推论或三角形一边平行线的性质定理
平行于三角形一边的直线截其它两边(或两边的延长线),所得的对应线段成比例。
若
DE∥BC
若
AF∥BC
则: 则:
A
X
能力目标小结
1
、
平行线分线段成比例定理是研究相似形最重要、最基本的理论基础,而字母
A
型、
字母
X
型又是解决相似三角形一章有关计算和证明的模具,可构造或寻找字母
A
型、字母
X
型解决问题,把它称为三角形相似问题“奠基法” 。
2
、学会用“动态”的观点去解决研究问题。
3
、欣赏模型
“
字母
A
型、字母
X
型
”
的理性美、结构美,诱发学习数学的激情,感受数学的美学文化,培养学生
“
自主实践、自主探索、大胆猜想、归纳创新
”
的数学理念。
补充练习
1.
已知
:
点
E
在平行四边形
ABCD
的边
AB
的延长线上,
DE
分别交
AC
、
BC
于点
F
、
G
,在图中找出字母
A
型图、字母
X
型图。
A
B
E
D
C
G
F
图
10
答案(
3
)
字母
A
型图
字母
X
型图
A
B
C
D
E
F
G
A
B
C
D
E
F
G
A
B
D
C
E
F
G
图
10-1
图
10-3
图
10-4
图
10-2
A
D
B
C
F
G
E
作业
1
、如图:∠
A=∠C
,
AB/BC=3/2
,
BE=8
。求
BD=
?
2
、已知:
FG∥AE∥BC
,
GH∥CD
,求:
AF/BF=EH/HD
A
D
E
C
B
A
B
C
E
D
F
G
H
再见
再见
再见