高中数学选修2-1课件2_3_1抛物线的定义与标准方程 28页

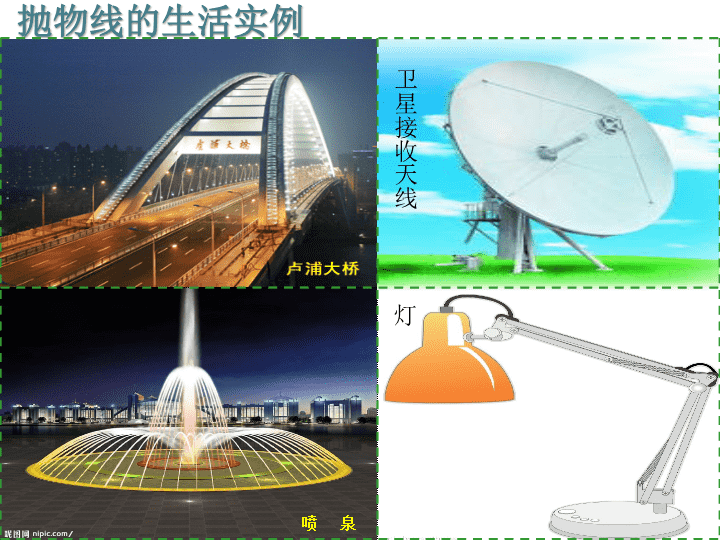
抛物线的生活实例 喷 泉 灯 卫星接收天线 平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹叫做 抛物线 . 定点 F 叫做抛物线的 焦点 , 定直线 l 叫做抛物线的 准线 . 1. 抛物线的定义 F M l N · · 几何关系式 代数关系式 解析法 即 : ︳ ︳ ︳ ︳ 求曲线方程的基本步骤是怎样的？ 2. 探究抛物线的标准方程 l F M N · · 建系 列式 化简 检验 设点 解法一：以 l 为 y 轴，过点 F 垂直于 l 的直线为 X 轴建立直角坐标系（如下图所示） , 记 |FK| ＝ p, 则定点 F(p,0), 设动点 M(x,y) ，由抛物线定义得：  化简得 ： x o y l F M(X,y) K 解法二 : 以定点 F 为原点 , 过点 F 垂直于 l 的直线为 X 轴建立直角坐标系 ( 如下图所示 ), 记 |FK|=P, 则定点 F(0,0), l 的方程为 X= - P 设动点 ，由抛物线定义得 ： 化简得 ： K F M ( x , y ) x y 解法三：以过 F 且垂直于 l 的直线为 x 轴 , 垂足为 K. 以 F,K 的中点 O 为坐标原点建立直角坐标系 xoy. 依题意得 两边平方 , 整理得 K F M ( x , y ) y o x F M( x ,y) ● K x o y K F M ( x , y ) x y K F M ( x , y ) y o x 比较探究结果： 方程最简洁 抛物线的标准方程 方程 y 2 = 2p x （p＞0） 表示抛物线，其焦点 F 位于 x 轴的正半轴上，其准线交于 x 轴的负半轴 P 的几何意义是 : 焦点到准线的距离 ( 焦准距 ) ， 故此 p 为正常数 y x o . F p 即 焦点 F ( ,0 ) 准线 l ： x = 3. 抛物线的标准方程 抛物线的标准方程还有哪些形式? 其它形式的抛物线的焦点与准线呢？ 4. 探究抛物线的标准方程的其它成员 x y l o F x y o l F x y l o F x y l o F 方案三 方案二 方案一 方案四 y x o . F y x o . F y x o . F y x o . F 类比 分析 （ - x ） 2 2py ＝ Ｆ (0, ) y 2 =-2px (p>0) x 2 =2py (p>0) 准线方程 焦点坐标 标准方程 图 形 x F O y l x F O y l x F O y l x F O y l y 2 =2px (p>0) x 2 =-2py (p>0) P 的意义 : 抛物线的焦点到准线的距离 方程的特点 : (1) 左边 是二次式 , (2) 右边 是一次式 ; 决定了 焦点的位置 . 5. 四种抛物线的特征 — 区别与联系   焦点坐标 准线方程 (1) (2) (3) (4) （ 5 ， 0 ） x = - 5 （ 0 ， - 2 ） y =2 5/8 (-5/8, 0) y=-1/8 (0 , 1/8) 5. 四种抛物线的特征 — 知识巩固和迁移 6. 例题讲解 1-- 例题 1 （抛物线的定义） 例 2 （ 1 ）已知抛物线的标准方程是 y 2 = 6 x ， 求它的焦点坐标及准线方程； （ 2 ）已知抛物线的焦点坐标是 F （ 0 ，－ 2 ）， 求抛物线的标准方程； 焦点 F ( , 0 ) 3 2 准线： x = － 3 2 抛物线的标准方程 x 2 = － 8 y 解 (1) 2p=6 p/2=3/2 (2) p/2=2, 2p=8 6. 例题讲解 2--- 例题 2 （抛物线的标准方程） Ex: 焦点在直线 x-2y-4=0 上 . 解读例 5 （解读例 8 ） 抛物线 的顶点在原点，焦点在 x 轴上，其上有一点 A(4,m) , 到其准线的距离为 6 ，则 m=__________. 例 3 ：求过点 A（-2，4） 的抛物线的 标准方程。 A O y x 解：1）设抛物线的标准 方程为 x 2 =2py， 把 A（-2，4） 代入 ， 得 　　　　　　　　　　　　 　　　 　　　　　 p=1/2 2）设抛物线的标准方程为 y 2 = -2px， 把 A(-2，-4) 代入 , 得 p=4 ∴ 抛物线的标准方程为 x 2 = y 或 y 2 =-8x . 6. 例题讲解 3 （解读例 5 、 6 方程 --- 分类讨论） 6. 例题讲解 3 （ 抛物线标准 方程 --- 分类讨论） 例 4 一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线，经反射聚集到焦点处。已知接收天线的径口（直径）为 4.8m ，深度为 0.5m 。建立适当的坐标系，求抛物线的标准方程和焦点坐标。 分析 : 0.5 4.8m 6. 例题讲解 4 — 实际应用题 解：如上图，在接收天线的轴截面所在平面 内建立直角坐标系，使接收天线的顶点（即抛物线的顶点）与原点重合。 设抛物线的标准方程是 y 2 =2px (p>0) ， 由已知条件可得，点 A 的坐标是 (0.5,2.4) ，代入方程，得 2.4 2 =2p×0.5, ∴p=5.76 ∴所求抛物线的标准方程是 y 2 =11.56 x ， 焦点的坐标是 (2.88,0) 4.8m (0.5,2.4) 0.5 作业：同步导学 P 36 11 、 12 6. 例题讲解 4 — 实际应用题 例 5. （同步导学 34 页例 2 ） 已知点 P 是抛物线 x 2 ＝ 8 y 上的一个动点， F 是抛物线的焦点，定 点 M (-2,4) ， 求 | PM | ＋ | PF | 的最小值． 6. 例题讲解 5 拓展迁移 — 最值问题与几何解法 7. 精华考题选粹 --- 考场零距离 代数方法比几何方法更有说服力，更容易接受 ! 代数方法比几何方法更有说服力，更容易接受 ! 4. 标准方程中 p 前面的 正负号 决定抛物线的 开口方向 ． 1. 抛物线的定义 : 2. 抛物线的标准方程有四种不同的形式 : 每一对焦点和准线对应一种形式 . 3. p 的几何意义是 : 焦 点 到 准 线 的 距 离 作业：同步导学 P 36 11 、 12