高三数学同步辅导教材(第7讲) 10页

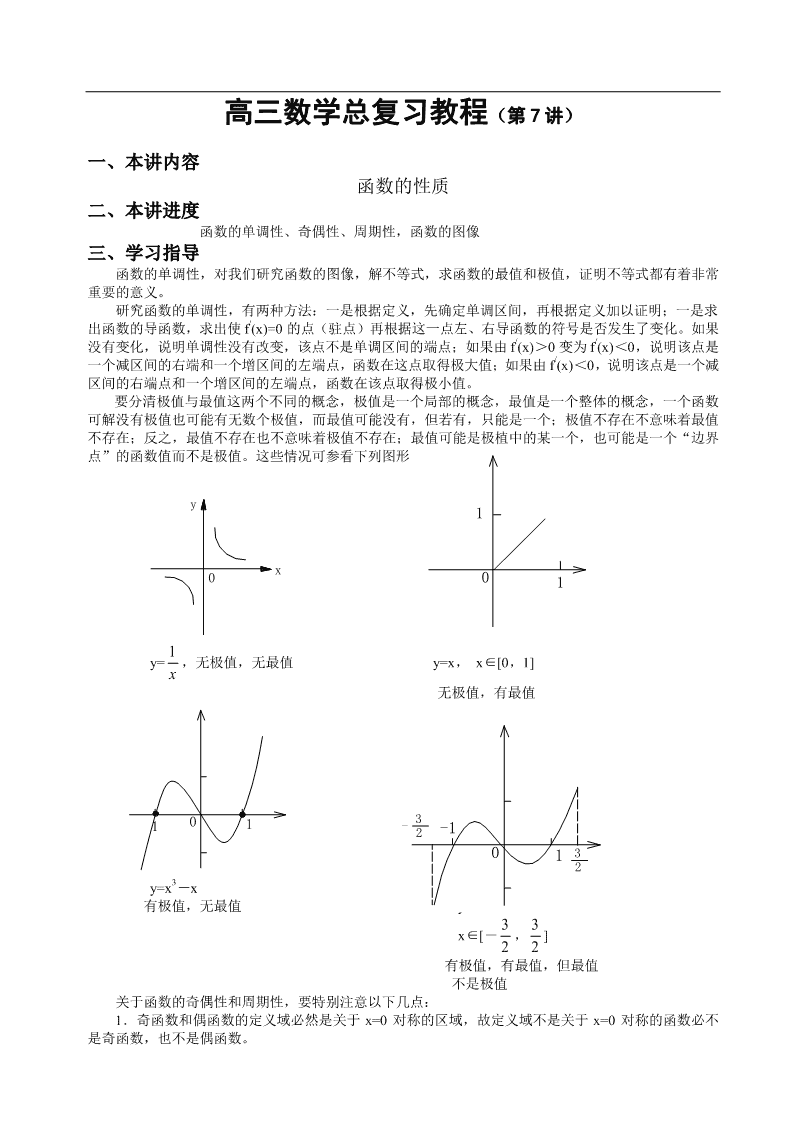
高三数学总复习教程（第 7 讲） 一、本讲内容 函数的性质 二、本讲进度 函数的单调性、奇偶性、周期性，函数的图像 三、学习指导 函数的单调性，对我们研究函数的图像，解不等式，求函数的最值和极值，证明不等式都有着非常 重要的意义。 研究函数的单调性，有两种方法：一是根据定义，先确定单调区间，再根据定义加以证明；一是求 出函数的导函数，求出使 f/(x)=0 的点（驻点）再根据这一点左、右导函数的符号是否发生了变化。如果 没有变化，说明单调性没有改变，该点不是单调区间的端点；如果由 f/(x)＞0 变为 f/(x)＜0，说明该点是 一个减区间的右端和一个增区间的左端点，函数在这点取得极大值；如果由 f/(x)＜0，说明该点是一个减 区间的右端点和一个增区间的左端点，函数在该点取得极小值。 要分清极值与最值这两个不同的概念，极值是一个局部的概念，最值是一个整体的概念，一个函数 可解没有极值也可能有无数个极值，而最值可能没有，但若有，只能是一个；极值不存在不意味着最值 不存在；反之，最值不存在也不意味着极值不存在；最值可能是极植中的某一个，也可能是一个“边界 点”的函数值而不是极值。这些情况可参看下列图形： y= x 1 ，无极值，无最值 y=x， x∈[0，1] 无极值，有最值 y=x3－x 有极值，无最值 y=x3－x x∈[－ 2 3 ， ] 有极值，有最值，但最值 不是极值 关于函数的奇偶性和周期性，要特别注意以下几点： 1．奇函数和偶函数的定义域必然是关于 x=0 对称的区域，故定义域不是关于 x=0 对称的函数必不 是奇函数，也不是偶函数。 0 x y 0 1 1 101 2 1 2 3- -1 0 3 2．奇函数的图像至于原点对称，偶函数的图像关于 y 的轴对称。注意“图像关于原点对称的函数必 是奇函数”与“关于原点对称的图形必是奇函数的图像”的区别。 3．在 x=0 处有定义的奇函数必满足 f(0)=0，即图像过原点（想一想，为什么？） 4．奇函数，偶函数仅仅是图像的对称中心，对称轴位置较特殊的函数，奇函数，偶函数的图像经过 平移后，未必还表示奇、偶函数，而不是奇函数，偶函数的函数，只要它们的图像是轴对称图形或中心 对称图形，就可经适当平移，成为奇（偶）函数的图像。 5．定义域有界的函数不可能是同期函数。同期函数不一定有最小正周期。若 T（T≠0）是函数 y=f(x) 的周期，则 T 的非零整数倍也是它的周期。 6．一个函数的图像，如果有两条对称轴：x=a 和 x=b（a≠b）就必有无数条对称轴，∵f(x)=f(2a－ x)=f(2b―(2a―x))=f(2b－2a+x)，∴ f(x)为周期函数 2(b－a)为它的一个周期；如果有两个对称中心：（a，0）， （b，0）（ a≠b），则有无数个对称中心，设（x，y）为函数 y=f(x) 图像上任意一点，则(2a―x，―y)在 函数图象上，从而[2b―(2a―x)，―(―y)]即（2b―2a+x，y）也在函数图像上，∴f(x)为周期对称，2(b－ a)当它的一个周期；如果有一条对称轴 x=a 和一个对称中心(b，0)（a≠b）则函数图像也有无数条对称轴 和无数个对称中心，设(x―y)当函数图像上任意一点，则(2a―x，y)在图像上，(2b―2a+x，― y)在图象上， 从而 f(4b―4a+x)=f(x)，∴f(x)当周期函数 4b―2a 当其一个周期。 7．两个单调性相同的函数的和在它们的公共定义域内仍保持原来的单调性；当 a＞0 时，单调函数 f(x)与 af(x)有相同的单调性，当 a＜0 时，单调函数 f(x)与 af(x)有相反的单调性； 8．若函数 f(x)在 A 上单调，值域为 B，函数 g(x)在 B 上单调，则复合函数 g[f(x)]在 A 上单调，当 前两者单调性相同时，复合函数 g[f(x)]单调增，前两者单调性相反时，复合函数 g[f(x)]单调减。 9．同为奇（偶）函数的两函数，在其公共定义域内的和或差仍为奇（偶）函数，同奇偶的两函数的 积（商）在其公共定义域内为偶函数，一个奇函数与一个偶函数的积（商）在其公共定义域内与奇函数， 由奇、偶函数复合而成的函数中，有奇数个奇函数，复合函数才是奇函数，否则就是偶函数。 10．若 f(x)有反函数 f—1(x)，则 f(x)与 f/(x)在相应的区间中有相同的单调性；奇函数的反函数（如果 有反函数的话），仍为奇函数，偶函数一般没有反函数（除非它的定义域为 0 ）. 以上规律，想一想，为什么？你会证明吗？ 11．把函数 y=f(x)的图像按向量 a =（m，n）平移后图像对应解分析式为 y―n=f(x―m)，变即 y=f(x －m)+n. 把函数 y=f(x)的图像每一点纵坐标变为原来的 A 倍，横坐标不变，新图像的解析式，为 y=Af(x)；把 函数 y=f(x)图像上每一点横坐标变为原来的  1 倍，纵会标不变，新图像的解析式为 y=f(ω x)； 把函数 y=f(x)图像沿 x 轴翻转 1800，新图像解析式为 y=－f(x)；沿 y 轴翻转 1800，新图像解析式为 y=f(－x)；把函数 y=f(x)图象上 x 轴上方（含 x 轴上）的部分保持不变，下方的部分沿 x 轴翻转 1800，所 得新图形解析式为 y= )(xf ；保持图形在 y 轴右边（含 y 轴上）的部分不变，左方部分取消改为右方关 于 y 轴对称的图形，新图形的解析式为 y=f( x ) 四、典型例题讲评 例 1．判断下列函数的奇偶性： （1）f(x)= xx xx sincos1 cossin1   （2）f(x)= 1xa a + 2 x （a＞0 且 a≠1） 这两个函数的解析式都很难直接看出奇偶数，但绝不能据此下“不是奇函数，也不是偶函数”的结 论，因为形式经过恒等变形后有可能直接可以判断。例如（2）中 f(x)= · 1 1   x x a a ∵ 1 1     x x a a = x x a a   1 1 =－ 1 1   x x a a ，可知 f(x)为两个奇函数之积，在其定义域 0 xRxx 且 中为偶函 数，（1）中 f(x)= 2cos2sin22cos2 2cos2sin22sin2 2 2 xxx xxx   = )2sin2(cos2cos2 )2cos2(sin2sin2 xxx xxx   =tan 2 x ，此时从形式上看应为奇函数， 但因约去了因式ε · +cos ，故应加注使ε · +cos≠0，即 ≠kπ － 4  ，即 x≠kπ － 2  （k∈Z） 这显然关于原点不对称，故结论为“不是奇函数，也不是偶函数”其实这一点在一开始求定义域 1+cosx+sinx≠0 时即可得知。 综上，要判断一个函数的奇偶性，应先求其定义域，如定义域不关于原点对称，即可下“非奇、非 偶”的结论，如对称，再进一步考虑，或进行恒等变形，变成我们熟悉的情况加以判断，或利用定义， “若 f(x)+f(－x)≡0 则 f(x)当奇函数，f(x)―f(―x)≡0 为则 f(x)为偶函数 例 2．已知 2 为函数 y=f(x)的一个周期，当 x∈[0，2]时，f(x)= 1x ，求证 f(x)为偶函数。 本题没有给出[0，2]外的函数表达式，如何判断奇偶性？故应先据 T=2，写出一般区间[2k，2(k+1)] 上函数表达式，再看[―2(k+1)，―2k]上的表达式与之是否有 f(x)+f(―x)≡0 或 f(x) ―f(―x)≡0 的关系， 具体解法参看附录 例 3．已知函数 h(x)=2x，y=g(x)为它的反函数，y=g(x)的图像上有横坐标分别为 a，a+4，a+8 的三 点，A、B、C（a＞1）,△ABC 的面积记为 S。 （1）求 S=f(a)的表达式； （2）求 S=f(a)的值域； （3）判断 S=f(a)的单调性 g(x)=log2x，关键是△ABC 面积，怎样求 设 A、B、C 在 x 轴上的射影是 A/、B/、C/ 则 ABCS = BBAAS //梯形 + CCBBS //梯形 － CCAAS //梯形 = 2 )4(loglog 22  aa ×4+ 2 )8(log)4(log 22  aa ×4 － 2 )8(loglog 22  aa ）×8 =2[2log2(a+4) －log2a－log2(a+8)]=2log2 )8( )4( 2   aa a 值域和单调性只要考虑 aa aa 8 168 2 2   ，亦即只要考虑 aa 8 1 2  的值域和单调性就可以了。 例 4．已右函数 f(x)= 12 2   x x a 是奇函数，解关于 x 的不等式； )(1 xf  ＜m， 先根据 f(x)为奇函数，求得 a=－1，从而求得 )(1 xf  =log2 x x   1 1 ，x∈(－1，1). 不等式即 x x   1 1 ＜2m，0＜ x1 2 ＜2m+1， －1＜x＜1－ 12 2 m 例 5．当点 P（x，y）在函数 f(x)=loga(x－3a)（a＞0 且 a≠1）的图像上运动时点 Q（x－2a，－y） 运动的轨迹为函数，函数 y=g(x)的图像 （1）写出 g(x)的解析式； （2）若当 a∈(0，1)，x∈[a+2，a+3]时， )()( xgxf  ≤1 恒成立，试确定 a 的取值范围。 解：当 P（x，y）为 g(x)图像上任一点时，P/(x+2a，－y)在 f(x)图象上故有－y=loga(x+2a－3a)得出 f(x)= －loga(x－a) = )(log)3(log axax aa  ≤1 要恒成立，应有      aaxaxa ax 1))(3( 3 ，当 x∈[a+2，a+3]时恒成立. y=(x－5a)(x－a)在(3a，+∞)单调递增，而圆 a∈(0，1)知 a+2＞3a.故      aaaaa aaaaa 1)3)(33( )2)(32( ，解得 a∈        12 579,0 例 6．已知函数 f(x)的图像与曲线 C 关于 y 轴对称，把曲线 C 按向量 a (－1，0)平移后，恰为函数 y= )2(log 2 x 的图像. （1）求 y=f(x)的解析式及其定义域； （2）若 1＜a＜b，f(a)＜f( 1b b )，则 a＜2＜b； （3）在（2）中，若 f(b)=2f( 2 ba  )，则 4＜b＜3+ 2 （1）先把 y= )2(log 2 x 按b =（1，0）平移，得到曲线 C 的解析式：y= )1(log 2 x ∴f(x)= )1(log 2 x ，定义域为（1，+∞） 当 x∈ 2,1 时，f(x)=－log2(x－1)单调递减；当 x≥2 时，f(x)=log2(x－1)单调递增。 （2）条件即 )1(log 2 a = )11(log 2 b b = 1 1log 2 b = )1(log 2 b 又 1＜a＜b，故 a≠b ∴ 1 1 a =b－1. ∴b－1＞1，a－1∈（0，1） 从而 a＜2＜b； （3） 2 ba  －1= 2 1 （a－1+b－1）= （ 1 1 b +b－1）＞1（∵b－1＞0） ∴log2(b－1)=2log2 （ +b－1），令 1b =t＞1，则 t4－2t3+1=0 约去 t－1（C≠0） t5－t2－t－1=0 证 g(t)=t3－t2－t－1，g( 3 )=2 －4＜0，g( 22  )= (1+ )－(3+ )＞0 g/(t)=3t2－2t－1，当 t＞1 或 t＜－ 3 1 为正. 说明 g(t)在 ,1 单调递增 令 t＞1 ∴t∈( ， ) 即 b∈（4，3+ ）. 巩固练习 1．y=f(1－3x)的图像不能由 y=f(x)经由下列变换中的（ ）得到 （A）向右平移 1 个单位，每点纵坐标不变，横坐标变为原来的－ （B）每点纵坐标不变，横坐标变为原来的－ 3 1 ，向右平移 1 个单位； （C）绕 y 轴旋转 1800，左移 1 个单位后每点纵坐标不变，横坐标变为原来的 （D）绕 y 轴旋转 1800，每点纵坐标不变，横坐标变为原来的 ，右移 . 2．已知 y=f(x)是奇函数，在（－∞，0）上单调递减，则函数 y=f(1－ x )满足（ ） （A）是奇函数在（－∞，－ 2 1 ）单调递增. （B）是增函数在（－∞，－ ）单调递减 （C）不是奇函数，也不是偶函数，在（－∞，－ ）单调递减 （D）是偶函数在（－∞，0）单调递减 3．作函数 y= 1 1   x x 的草图 4．设函数 f(x)是 k 上的增函数，若不等式 f(1－ax－ax2)＜f(2－a)对于任意的，x∈[0，1]都成立， 求 a 的取值范围. 5．已知 f(x)= 12   bxx ax 是奇函数 （1）求 a、b 的值 （2）判断 f(x)的单调区间，并加以证明。 （3）求 f(x)的值域 6．函数 y=f(x)定义在非零实数集上，且对定义域内任意的 x1，x2，都有 f(x1，x2)=f(x1)+f(x2)，试判 断 y=f(x)的奇偶性 7．已知 y=f(x)是 k 上的偶函数，当 x≤－1 时，图像为斜率为 1，经过（－2，0）点的射线，又知图 像的后部分是以（0，2）为顶点过（－1，1）的抛物线的一部分，求函数 y=f(x)的解析式. 8．x、y∈[－ 4  ， 4  ]，且      0cossin4 02sin 3 3 ayyy axx ，求 cos( 2 x +y)的值. 9．已知 y=f(x)是 k 上的偶函数，f( 2 3 －x)=f( +x)；对任意的 x1、x2∈[0， ]，都有 f(x1+x2)=f(x1)(x2)， 且 f(1)=a＞0 （1）求 f( )、f( 4 1 )的值. （2）若在[0，1]上 f(x)是基本初等函数，求其解析式. 10．设 f(x)= 12 x －ax（a＞0） （1）解不等式：f(x)≤1 （2）求 a 的取值范围，使函数 y=f(x)在 ,0 上单调. 11．设 f(x)定义在（0，1）上，函数值恒正，对任意的 x1，x2∈（0，1），恒有 )( )( 2 1 xf xf = )1( )1( 2 1 x xf   ≤2 。 （1）求证：对任意的 x∈（0，1），恒有 f(x)=f(1－x) （2）求函数 g(x)= x xf )( 的值域和单调性 12．定义在 R 上的函数 f(x)满足：f(a+b)≡f(a)+f(b)，（ a，b 为任意实数），又当 f＞0 时，f(t)＜0 ①求 f(0)，并判断 f(x)的奇偶数； ②若 f(1)=－2，求 f(x)当 x∈[－3，3]时的取值范围. 五、参考答案 1．B 2．B 3．y=             1 1 1 1 1 x x x x 1 )0,1( 0    x x x 当 当 当 4．1－ax－ax2＜2－a. 即 ax2+ax+1－a＞0 当 a=0 时，即 1＞0，当然成立 当 a＜0 时，须       01 01 045 2 a a aa ， ∴a∈(－1，0) 当 a＞0 时，须△≤0， 即 a∈[0， 5 4 ] 或      01 5 4 a a ，即 a∈( ，1)， ∴a∈ 1,0 总之，a∈（－1，1） 解法二 1－ax－ax2＜2－a， 即 a(x2+x－1)＞－1 ① 当 x= 2 15  时，x2+x－1=0 ①式当然成立. 当 x∈        2 15,0 时，a＜ 1 1 2   xx ，此时右边∈[1，+∞] ∴a＜+1， 当 x∈        1,2 15 时，a＞ 1 1 2   xx ，此时右边∈ 1, ∴a＞－1， 总之，a∈（－1，1）. 5．（ 1）∵f(x)是奇函数，∴ 12   bxx ax + 12   bxx ax ≡0. 化简得(a+b)x2+a≡0. ∴      0 0 ba a ，即 a=b=0. （2）由（1）知 f(x)= 12 x x 对任意的 x1＜x2，y1－y2= )1)(1( )1)(( 2 2 2 1 2121   xx xxxx ,易知， 当 x1，x2∈ 1, 或 ,1 时，y1－y2＞0，而当 x1，x2∈[－1，1]时，y1－y2＜0，故 f(x)在[－1， 1 -1 0-2 -1 1 x y 3 1]上单调递增，而在 1, 及 ,1 单调递减. (3)∵x2+1≥2 x ，∴ 12 x x ∈[－ 2 1 ， ]. 6．令 x1=x2=1，知 f(1)=0，令 x1=x2=－1，知 f(－1)=0 令 x1=x，x2=－1，知 f(－x)=f(x)，∴f(x)为偶函数 7．当 x≤－1 时，f(x)=x+2，故当 x≥1 时，因 f(x)为偶函数，故 f(x)=f(－x)= －x+2； 当 x∈（－1，1）时，y=ax2+2，过（－1，1），∴a=1 ∴f(x)=       2 2 2 2 x x x 1 )1,1( 1    x x x当 8．由已知 2x + x =(－2y)3+ε ·(－2y)=2a. 又函数 f(t)=t3+sint 在[－ 2  ， 2  ]单调递增。 ∴x=－2y， ∴ 2 x +y=0， cos（ +y）=1, 9.由已知，f[1+( －x)]=f[1－( －x)]，知 f(1+x)=f(1－x) x=1 是 y=f(x)图像的一条对称轴，∵f(x)为偶函数， ∴f(x)=f(－x)=f[1－(x+1)]=f[1+(x+1)]=f(x+2) ∴f(x)为周期函数，T=2 为其一周期. （1）a=f(1)=f( + )=[f( )]2， ∴f( 2 1 )=± a ，但 f( )=f( 4 1 + )=[f( )]2，∴f( )= ，类似 地 f( )= 4 a . （2）基本初等函数中，仅指数函数满足 f(x1+x2)=f(x1)f(x2) ∴在 x∈[0，1]时，f(x)=ax，从而当 x∈[－1，0]时，f(x)=a—x 当 x∈[2k－1，2k+1] （k∈Z）时， f(x)=      )2( )2( kx kx a a  12,2 ]2,12[   kkx kkx 当 当 10．（ 1）令 12 x －ax≤1，则 12 x ≤ax+1，同解于      02)1( 01 22 axxa ax 10，当 a∈(0，1)时，即        ]1 2,0[ 1 2a ax ax ，∴x∈[0， 21 2 a a  ]， 20，当 a∈（1，+∞）时，即         21 20 1 a axx ax 或 ， ∵ 21 2 a a  －(－ a 1 )= 2 2 1 1 a a   ＜0，∴x∈ ,0 30， 当 a=1 时，即      0 1 x x ，∴∈ （2）f(x)= axx xa   2 22 1 1)1( ∵y= 21 x +ax（x∈ ,0 ），当 a＞0 时值，恒正且单调递增 而当 a=1 时，y=(1－a2)x2+1≡1，为正常数， 当 a＞1 时，y=(1－a2)x2+1 在 单调递减 ∴当 a≥1 时，原函数 y=f(x)在 单调递减 当 a∈（0，1）时，由（1）知 f(0)=f( 21 2 a a  )=1 不可能在 上单调 ∴a∈ ,1 11．(1)当 x∈（0，1）时，1－x∈(0，1)，令 x1=x，x2=1－x，由 已知有 )1( )( xf xf  + )( )1( xf xf  ≤2 但因 f(x)＞0，∴ ＞0，∴ + ≥2 ∴ + =2，且 = ∴f(x)=f(1－x)=1 （2） 由（1）知，当 x∈（0，1）时，f(x)=1，∴g(x)= x 1 ，在（0,1）单调递减 g(x)∈（1，+∞） 12． （1）令 a=b=0，知 f(0=2f(0)) ∴f(0)=0 令 b=－a，则有 f(0)=f(a)+f(－a)=0，∴f(－a)= －f(a) ∴f(x)为奇函数 （2）令 b＞0，则 f(a+b)=f(a)+f(b)＜f(a)，故 f(x)单调递减 又 f(3)=f(1)+f(2)=3f(1)= －6 ∴当 x∈[－3，3]时，f(x)∈[－6，6] 六、附录 例 1．（ 1）令 1+cosx+sinx=0，即 2cos2 2 x +2sin cos =0 cos (cos +sin )=0，cos =0 或 tan =－1 x=(2x+1)π 或 x=2kπ － 2  ，（ k∈Z） 故原函数定义域为        ZkkxkxRxx ,22)12( 且且 关于原点不对称，∴f(x)既非 奇函数，也非偶函数 (2) f(－x)= 1  xa x + 2 x = x x a xa   1 － = x x a xax   1 )1( － = + 1xa x =f(x) ∴f(x)为偶函数 例 2．对任意的 x∈R，必存在整数 k，使 x∈[2k，2k+2]，则－x∈[－2k－2，－2k]， 又 T=2，∴2k 亦为 f(x)的周期，∴f(x)=f(x－2k)= 12  kx f(－x)=f(－x+2k+2)= 122  kx = =f(x) ∴f(x)为偶函数 例 3．g(x)=log2x，当 a＞1 时，△ABC 的面积可看作梯形 AA/B/B 与梯形 BB/C/C 的面积之和减去梯 形 AA/C/C 的面积. （A/、B/、C/分别为 A、B、C 在 x 轴上的射影） ∴ f(a)= 2 )4(loglog 22  aa × 4+ 2 )8(log)4(log 22  aa × 4 － 2 )8(loglog 22  aa × 8=2log2 )8( )4( 2   aa a ，（ a＞1） ∵ )8( )4( 2   aa a =1+ )8( 16 aa 在（1，+∞）单调递减，故取值范围为（1， 9 25 ），从而 f(a)在(1，+∞) 单调递减，值域为（0，4(log25－log2)）. 例 4．∵f(x)为奇函数，∴ 12 2   x x a + 12 2     x x a =0，即 （1+a）(2x+1)≡0，∴a=－1，f(x)= 12 12   x x ，       12 12 )1,1( m m x x ∴x∈（－1， 12 12   m m ） 例 5．（ 1）设 Q（x，y）为 g(x)图像上任意一点，则(x+2a，－y)在 f(x)图像上，故有 －y=loga(x+2a－3a)，即 y=loga ax  1 （2） )()( xgxf  = )(log)3(log axax aa  ≤1 当 x∈[a+2，a+3] 时恒成立，即当 x∈[a+2，a+3]时，恒有      aaxaxa ax 1))(3( 3 ∵y=(x－3a)(x－a)在（3a，+∞）单调递增，而 a∈(0，1)时， a+2＞3a，所以      aaaaa aaaaa 1])3][(3)3[( ])2][(3)2[( 解得 a∈        12 579,0 例 6．（ 1）把 y= )2(log 2 x 的图像向右平移 1 个单位，故曲线 C 之解析式为 y= )2)1([log 2  x = )1(log 2 x f(x)的图象与曲线 C 关于 y 轴对称，∴f(x)= )1(log 2 x (x＞1) （2）当 x∈ 2,1 时，f(x)单调递减，当 x∈ ,2 时，f(x)单调递增. f(a)=f( 1b b ) 即 )1(log 2 a = )11(log 2 b b = )1(log 2 b 又 1＜a＜b，故 1 1 a =b―1 ，b―1＞1，a－1∈（0，1） ∴a＜2＜b （3） f(b)=2f( 1b b )，即 )1(log 2 b =2 )12(log 2  ba ∵b－1＞1，a－1= 1 1 b ，且 b－1≠1 ∴ )1(log 2 b =log2(b－1)， 2 )12(log 2  ba =2 2 11log 2  ba =2 )11 1(2 1log 2  bb =2log2 2 1 ( 1 1 b +b－1). ∴ log2(b－1)=log2 ( +b－1)， 1b = （ +b－1） 证 t= 1b ＞0，即知 t4―2t3+1=0，∵t―1≠0 ∴g(1)=t3―t2―t―1=0 ∵g( 3 )=2 ―4＜0，g( 22  )= [(2+ 2 )―1]―[(2+ )+1]= (1+ )― (3+ )= 2710  ― 2611 = )12(2611  － 2611 ＞0 g/(t)=3t2―2t―1 当 t＞1 时为正，∴t∈( ， 22  ) 即 b∈(4，3+ )