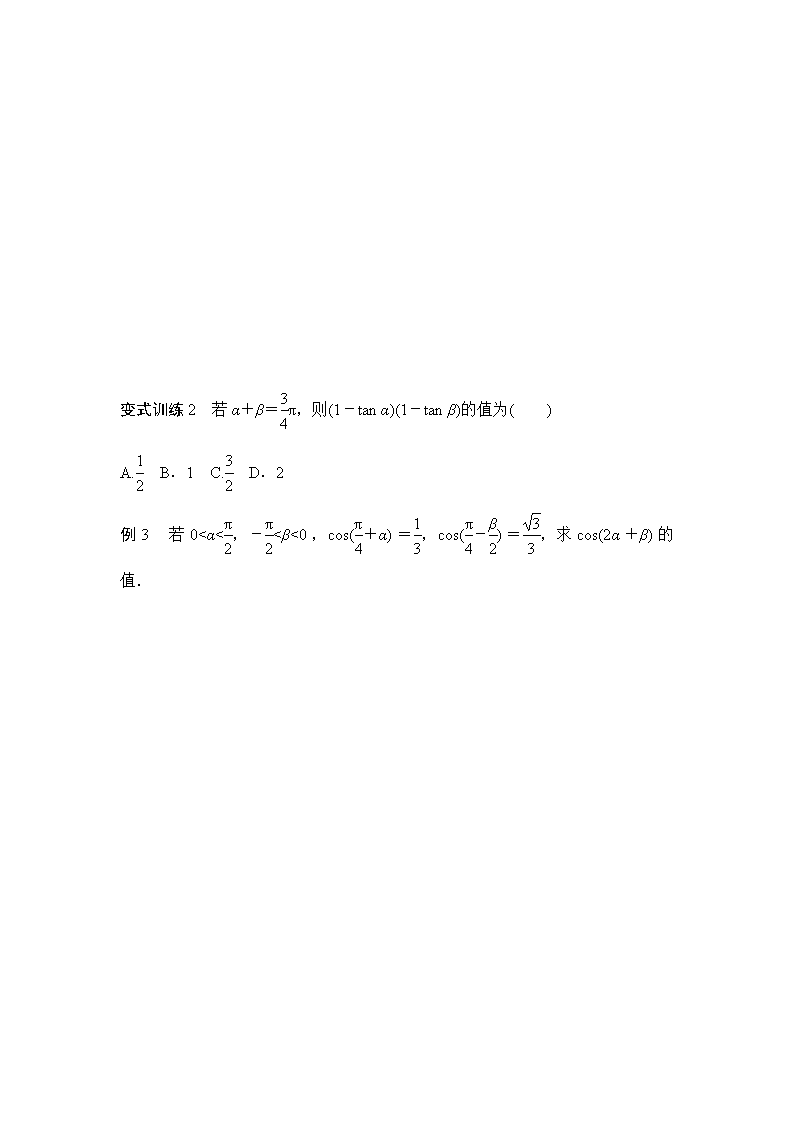【数学】2018届一轮复习人教A版专题12两角和与差的三角函数学案 10页

专题12　两角和与差的三角函数 两角之差的余弦：cos(α－β)＝cos αcos β＋sin αsin β，记为：C(α－β)；‎ 两角之和的余弦：cos(α＋β)＝cos αcos β－sin αsin β，记为：C(α＋β)；‎ 两角之和的正弦：sin(α＋β)＝sin αcos β＋cos αsin β，记为：S(α＋β)；‎ 两角之差的正弦：sin(α－β)＝sin αcos β－cos αsin β，记为：S(α－β)；‎ 两角之和的正切：tan(α＋β)＝，记为：T(α＋β)；‎ 两角之差的正切：tan(α－β)＝，记为：T(α－β)；‎ 二倍角公式：sin 2α＝2sin αcos α，记为S2α；‎ cos 2α＝cos2α－sin2α＝1－2sin2α＝2cos2α－1，记为C2α；‎ tan 2α＝，记为T2α.‎ ‎　　　　　　　　　　　　　　　　　　　‎ 例1　已知sin(＋)＝，求cos 2θ的值．‎ 变式训练1　已知α∈，sin α＝，则tan(α＋)等于(　　)‎ A. B．7 C．－ D．－7‎ 例2　化简：tan 13°＋tan 32°－tan 13°tan 32°.‎ 变式训练2　若α＋β＝π，则(1－tan α)(1－tan β)的值为(　　)‎ A. B．1 C. D．2‎ 例3　若0<α<，－<β<0，cos(＋α)＝，cos(－)＝，求cos(2α＋β)的值．‎ 变式训练3　若cos(α＋)＝－，α∈(0，)，求cos α的值．‎ A级 ‎1．若tan α＝，tan(α＋β)＝，则tan β等于(　　)‎ A. B. C. D. ‎2．若cos 2α＝，则sin4α＋cos4α等于(　　)‎ A．1 B. C. D. ‎3．若tan θ＝，则等于(　　)‎ A. B．－ C. D．－ ‎4．设α、β为锐角，sin α＝，sin β＝，则α＋β为(　　)‎ A. B. C.或 D．以上都不对 ‎5．如果cos θ＝－，θ∈(π，)，则cos(θ＋)的值是______．‎ ‎6.＝________．‎ ‎7．设sin 2α＝－sin α，α∈，则tan 2α的值是________．‎ B级 ‎8．tan 23°＋tan 37°＋tan 23°tan 37°等于(　　)‎ A. B．1 C．2 D. ‎9．设sin(＋θ)＝，则sin 2θ等于(　　)‎ A．－ B．－ C. D. ‎10．已知α、β均为锐角，且sin α＝，cos β＝，则α－β的值为________．‎ ‎11．比较大小：sin 36°＋cos 36°________sin 38°＋cos 38°.(填“>”，“<”或“＝”)‎ ‎12．已知sin α＝，sin(α－β)＝－，α，β均为锐角，求β的值．‎ ‎13．若cos(α＋β)＝，cos(α－β)＝，求tan α·tan β的值．‎ 专题12　两角和与差的三角函数 典型例题 例1　解　由sin(＋)＝，得sin ＋cos ＝，‎ 两边平方整理，得1＋sin θ＝，即sin θ＝－，‎ cos 2θ＝1－2sin2θ＝1－2×(－)2＝－.‎ 变式训练1　A　[∵α∈(，π)，sin α＝，‎ ‎∴cos α＝－ ＝－，∴tan α＝＝－，‎ ‎∴tan(α＋)＝＝.]‎ 例2　解　tan 13°＋tan 32°－tan 13°tan 32°‎ ‎＝tan(13°＋32°)(1－tan 13°tan 32°)＋tan 13°tan 32°‎ ‎＝tan 45°(1－tan 13°tan 32°)＋tan 13°tan 32°‎ ‎＝1－tan 13°tan 32°＋tan 13°tan 32°＝1.‎ 变式训练2　D　[(1－tan α)(1－tan β)＝1＋tan αtan β－(tan α＋tan β)①‎ ‎∵tan α＋tan β＝tan(α＋β)(1－tan αtan β)＝tan π(1－tan αtan β)＝tan αtan β－1，∴①式＝2，故选D.]‎ 例3　解　根据条件可得α＋∈(，)，－∈(，)，‎ 所以sin(α＋)＝，sin(－)＝，‎ 所以cos(2α＋β)＝cos 2[(α＋)－(－)]‎ ‎＝2[cos(α＋)cos(－)＋sin(α＋)sin(－)]2－1‎ ‎＝2(×＋×)2－1＝2()2－1＝.‎ 变式训练3　解　∵α∈(0，)，∴α＋∈(，)，‎ 又cos(α＋)＝－，故sin(α＋)＝ ＝，‎ cos α＝cos[(α＋)－]＝cos(α＋)cos ＋sin(α＋)sin ＝－×＋×＝.‎ 强化提高 ‎1．A　[tan β＝tan[(α＋β)－α]＝ ‎＝＝.]‎ ‎2．C　[sin4α＋cos4α＝(sin2α＋cos2α)2－2sin2αcos2α＝1－sin22α ‎＝1－(1－cos22α)＝1－(1－)＝，故选C.]‎ ‎3．A　[＝＝tan θ＝.]‎ ‎4．A　[α、β为锐角，sin α＝，sin β＝，‎ ‎∴cos α＝，cos β＝，∴cos(α＋β)＝cos αcos β－sin αsin β＝，‎ 又α、β为锐角，α＋β∈(0，π)，∴α＋β＝.]‎ ‎5．－ 解析　由cos θ＝－，θ∈(π，)知 sin θ＝－＝－ ＝－，‎ ‎∴cos(θ＋)＝cos θcos －sin θsin ＝(cos θ－sin θ)‎ ‎＝×(－)＝－.‎ ‎6. 解析　＝ ‎＝＝＝.‎ ‎7. 解析　∵sin 2α＝2sin αcos α＝－sin α，‎ ‎∴sin α(2cos α＋1)＝0，‎ 又α∈，∴sin α≠0，2cos α＋1＝0‎ 即cos α＝－，sin α＝，tan α＝－，‎ ‎∴tan 2α＝＝＝.‎ ‎8．A　[tan 23°＋tan 37°＋tan 23°tan 37°‎ ‎＝tan(23°＋37°)(1－tan 23°tan 37°)＋tan 23°tan 37°‎ ‎＝tan 60°(1－tan 23°tan 37°)＋tan 23°tan 37°＝.]‎ ‎9．A　[sin(＋θ)＝(sin θ＋cos θ)＝，‎ 将上式两边平方，得(1＋sin 2θ)＝，‎ ‎∴sin 2θ＝－.]‎ ‎10．－ 解析　∵α、β∈，‎ ‎∴cos α＝，sin β＝，‎ ‎∵sin α