2020届二轮复习平面几何在解三角形中的广泛应用课件（11张）（全国通用） 11页

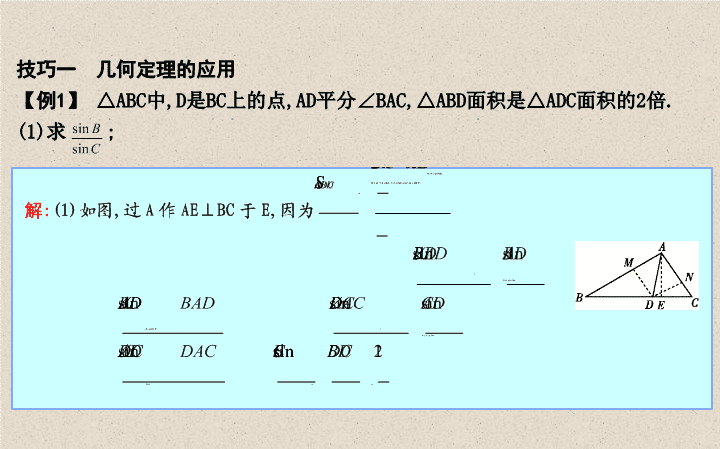
高考微专题四　平面几何在解三角形中的广 泛应用 解三角形问题就是分析和求解三角形的边、角大小,三角形特别是直角三角 形是平面几何中的最广泛的图形之一,在解三角形时,如能充分挖掘并利用图 形的几何性质,则能比较简捷地找到思路予以求解. 技巧一　几何定理的应用 【例1】 △ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC面积的2倍. (1)求 ;sin sin B C (2)若AD=1,DC= ,求BD和AC的长.2 2 方法点睛 三角形中的内角平分线定理、外角平分线定理、圆中相交弦定理、切割线 定理在实际解题中有很大的作用. 技巧二　构建和利用直角三角形 方法点睛 据几何图形的特征和题设条件,恰当作辅助线,构造直角三角形,利用勾股 定理、面积公式、直角三角形内角的三角函数可以有效地转化条件和结论, 达到解决问题的目的. 解析:∠BAD=∠BCD=90°, 即有∠BAD+∠BCD=180°, 所以四边形ABCD有外接圆☉O, 设☉O的半径为R, 则BD为直径等于2R. 方法点睛 构造出三角形或四边形(对角和为180°)的外接圆,利用点在圆(弧)上运 动或圆的性质,转化条件和结论,求面积的最大值或线段的长度,也是一种 解题的思路.