【数学】福建省三明市2020届高三普通高中毕业班质量检查（5月）（文）试题（A卷） 12页

福建省三明市2020届高三普通高中毕业班质量检查（5月）（文）试题（A卷）‎ ‎(试卷总分:150分考试时间:120分钟)‎ 注意事项:‎ ‎1.答题时，务必将自己的学校、班级.姓名、准考证号填写在答题卡规定的位置上 ‎2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮 擦擦干净后,再选涂其他答案标号.‎ ‎3.答非选择题时,必须使用黑色墨水笔或黑色签字笔,将答案书写在答题卡规定的位置上 ‎4.所有题目必须在答题卡上作答,在试题卷上答题无效.‎ ‎5.考试结束后,只将答题卡交回.‎ 第I卷(选择题,共60分)‎ 一、选择题(本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题要求的)‎ ‎1.设全集为,集合S={1,3,5} ,T={3 ,6},则等于 ( )‎ A.Φ B. {2,4,7,8} C. {1,3,5,6} D. {2,4,6,8}‎ ‎2.设复数z满足 (为虚数单位) ,则复数z为( )‎ A. . B. C. 1 D. 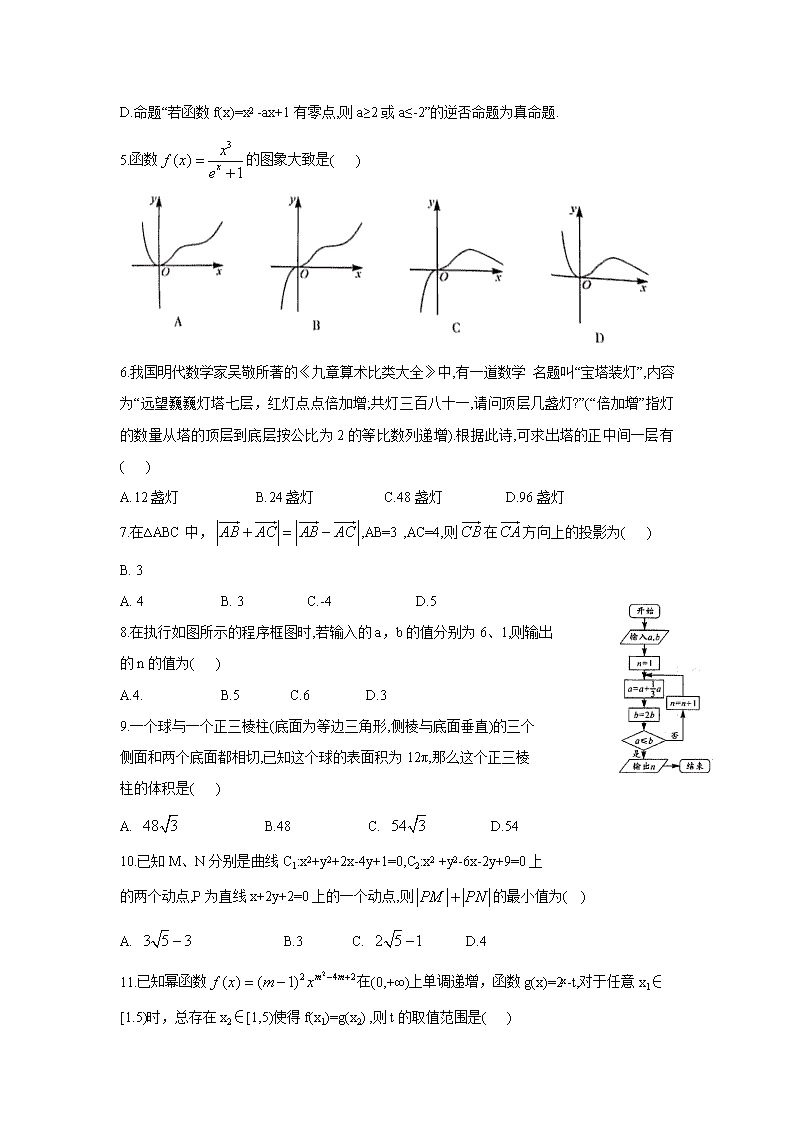-1-2i ‎3.某篮球队的甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个，命中个数的茎叶图如图,则下而结论中错误的是( )‎ A.甲命中个数的极差是29‎ B.甲命中个数的中位数是24‎ C.甲罚球命中率比乙高 D.乙命中个数的众数是21‎ ‎4.下列说法正确的是( )‎ A.命题“若x2=1,则x≠1的否命题是“若x2=1,则x=1"‎ B.命题“∈R, 的否定是“‎ C, y=f(x)在x0处有极值是的充要条件 D.命题“若函数f(x)=x2 -ax+1有零点,则a≥2或a≤-2”的逆否命题为真命题.‎ ‎5.函数的图象大致是( )‎ ‎6.我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学 名题叫“宝塔装灯”,内容为“远望巍巍灯塔七层，红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(“倍加增”指灯的数量从塔的顶层到底层按公比为2的等比数列递增).根据此诗,可求出塔的正中间一层有( )‎ A.12盏灯 B.24盏灯 C.48盏灯 D.96盏灯 ‎7.在∆ABC中，,AB=3 ,AC=4,则在方向上的投影为( )‎ B. 3‎ A. 4 B. 3 C.-4 D.5‎ ‎8.在执行如图所示的程序框图时,若输入的a，b的值分别为6、1,则输出 的n的值为( )‎ A.4. B.5 C.6 D.3‎ ‎9.一个球与一个正三棱柱(底面为等边三角形,侧棱与底面垂直)的三个 侧面和两个底面都相切,已知这个球的表面积为12π,那么这个正三棱 柱的体积是( )‎ A. B.48 C. D.54‎ ‎10.已知M、N分别是曲线C1:x2+y2+2x-4y+1=0,C2:x2 +y2-6x-2y+9=0上 的两个动点,P为直线x+2y+2=0上的一个动点,则的最小值为( )‎ A. B.3 C. D.4‎ ‎11.已知幂函数在(0,+∞)上单调递增，函数g(x)=2x-t,对于任意x1∈‎ ‎[1.5)时，总存在x2∈[1,5)使得f(x1)=g(x2) ,则t的取值范围是( )‎ A.Φ B.t≥7或t≤1 C. t>7或t0)上的两点,直线AB垂直x轴于点D,F为该抛物线的焦点,‎ 射线BF交抛物线的准线于点C,且, ∆AFC的面积为,则P的值为( )‎ A. B. 1 C.2 D.4‎ 第II卷(非选择题,共90分)‎ 二、填空题(本题共4小题，每小题5分,共20分)‎ ‎13.曲线在点(0,f(0))处的切线方程为________‎ ‎14.若x，y满足约束条件,则z=x+2y的最大值为______‎ ‎15.若且,则的值为_______‎ ‎16.设正项数列的前n项和Sn满足,且a2,a5,a14成等比数列,则 三、解答题(共70分解答应写出文字说明证明过程或演算步骤.第17 -21题为必考题，每个 试题考生都必须作答.第22、23题为选考题,考生根据要求作答)‎ ‎(一)必考题:共60分.‎ ‎17. (12分)已知∆ABC的周长为,且sin A+ sin B=sin C. .‎ ‎(1)求边AB的长;‎ ‎(2)若∆ABC的面积为sin C,求内角C的度数.‎ ‎18.(12分)某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试，根据 统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间的左侧，则认为 该学生属“体能不达标”的学生.其中 ,s分别为样本平均数和样本标准差,计算可得s≈27‎ ‎(同一组中的数据用该组区间的中点值作代表).‎ ‎(1)若该校高三某男生的跳远距离为187cm,试判断该男生是否属于“体能不达标”的学生;.‎ ‎(2)该校利用分层抽样的方法从样本区间[ 160 , 180) ,[ 180 ,200) ,[200 ,220)中共抽出5人，‎ 再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在[200,220)的概率 ‎19. (12分)已知在直三棱柱ABC-A1B1C1中, ∠ABC=90° ,AB= BC=2,侧而ACC1A1为正方形,P 为CC1的中点.‎ ‎(1)若在平面ABB1A1内存在动点R,满足RC1//平而APB，画出动点R的轨迹图形. (写出画 法)‎ ‎(2)在(1)向中画出的动点P的轨迹上任取一点Q,求三棱锥Q-ABP的体积 ‎20. (12分)设椭圆M: (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且椭圆的长轴长为4.‎ ‎(1)求椭圆M的标准方程;‎ ‎(2)若直线y=x+m交椭圆M于A, B两点,P(1,2)为椭圆M上一点,求∆PAB面积的最 大值.‎ ‎21. (12分)已知函数.‎ ‎(1)求函数f(x)的单调区间;‎ ‎(2)若∈(0, +∞) ,使不等式f(x)≤g(x)-ex成立,求a的取值范围.‎ ‎(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题 计分.‎ ‎22. [选修4-4:坐标系与参数方程](10分)‎ 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的长度单位建立 极坐标系,直线l的极坐标方程为,曲线C的参数方程为 ‎(为参数).‎ ‎(1)求直线l的直角坐标方程和曲线C的普通方程;‎ ‎(2)以曲线C上的动点M为圆心、r为半径的圆恰与直线l相切,求r的最大值.‎ ‎23. [选修4-5:不等式选讲](10分)‎ 已知a>0, b>0.‎ ‎(1)求证: ‎ ‎(2)若a>b , ab=2,求证: ‎