2018届二轮复习（理）指导三回扣溯源，查缺补漏，考前提醒模板五课件（全国通用） 13页

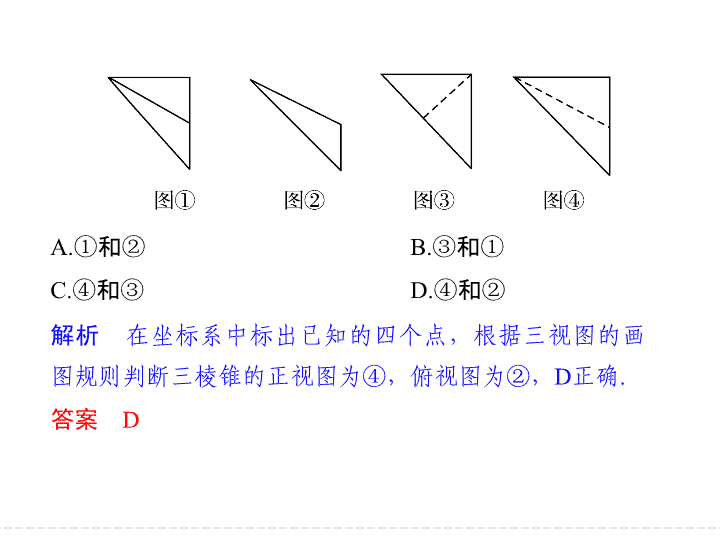
1. 由三视图还原为空间几何体的实际形状时，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线为虚线 . 在还原空间几何体实际形状时一般是以正 ( 主 ) 视图和俯视图为主 . [ 回扣问题 1] 　在如图所示的空间直角坐标系 O － xyz 中，一个四面体的顶点坐标分别是 (0 ， 0 ， 2) ， (2 ， 2 ， 0) ， (1 ， 2 ， 1) ， (2 ， 2 ， 2). 给出编号为 ① ， ② ， ③ ， ④ 的四个图，则该四面体的正视图和俯视图分别为 ( 　　 ) 溯源回扣五　立体几何 A. ① 和 ② B. ③ 和 ① C. ④ 和 ③ D. ④ 和 ② 解析　 在坐标系中标出已知的四个点 ， 根据三视图的画图规则判断三棱锥的正视图为 ④ ， 俯视图为 ② ， D 正确 . 答案　 D 3. 不清楚空间线面平行与垂直关系中的判定定理和性质定理，忽视判定定理和性质定理中的条件，导致判断出错 . 如由 α ⊥ β ， α ∩ β ＝ l ， m ⊥ l ，易误得出 m ⊥ β 的结论，这是因为忽视面面垂直的性质定理中 m ⊂ α 的限制条件 . [ 回扣问题 3] 　已知 m ， n 是不同的直线， α ， β ， γ 是不同的平面 . 给出下列命题： ① 若 α ⊥ β ， α ∩ β ＝ m ， n ⊥ m ，则 n ⊥ α 或 n ⊥ β . ② 若 α ∥ β ， α ∩ γ ＝ m ， β ∩ γ ＝ n ，则 m ∥ n . ③ 若 m 不垂直于 α ，则 m 不可能垂直于 α 内的无数条直线 . ④ 若 α ∩ β ＝ m ， n ∥ m ，且 n ⊄ α ， n ⊄ β ，则 n ∥ α ，且 n ∥ β . ⑤ 若 m ， n 为异面直线，则存在平面 α 过 m 且使 n ⊥ α . 其中正确的命题序号是 ________. 解析　 ① 错误 . 如正方体中面 ABB ′ A ′ ⊥ 面 ADD ′ A ′ ， 交线为 AA ′. 直线 AC ⊥ AA ′ ， 但 AC 不垂直面 ABB ′ A ′ ， 同时 AC 也不垂直面 ADD ′ A ′ ； ② 正确 . 实质上是两平面平行的性质定理 . ③ 错误 . 在上面的正方体中 ， A ′ C 不垂直于平面 A ′ B ′ C ′ D ′ ， 但与 B ′ D ′ 垂直 . 这样 A ′ C 就垂直于平面 A ′ B ′ C ′ D ′ 内与直线 B ′ D ′平行的无数条直线 . ④ 正确 . 利用线面平行的判定定理即可 . ⑤ 正确 . 如正方体中 AA ′ ⊂ 平面 AA ′ D ′ D ， 而 CD ⊥ 平面 AA ′ D ′ D ， 且 AA ′ 与 CD 异面 . 答案　 ②④⑤ 4. 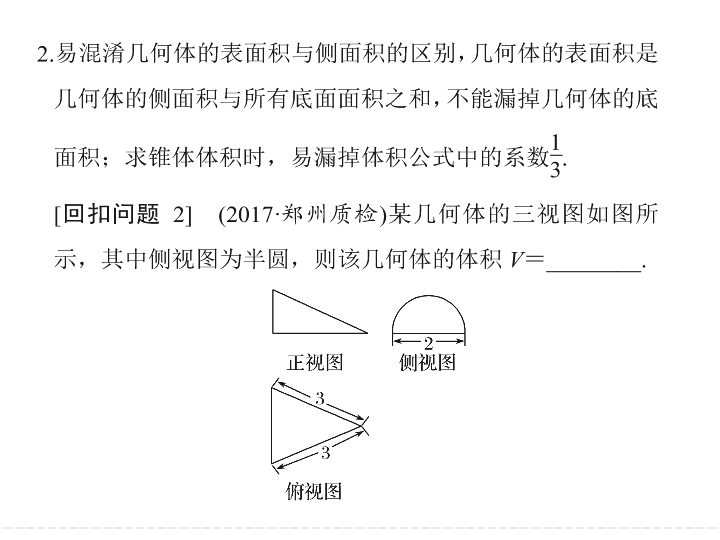忽视三视图的实、虚线，导致几何体的形状结构理解错误 . [ 回扣问题 4] 　如图，一个简单凸多面体的三视图的外轮廓是三个边长为 1 的正方形，则此多面体的体积为 ____________. 6. 注意图形的翻折与展开前后变与不变的量以及位置关系 . 对照前后图形，弄清楚变与不变的元素后，再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系 . [ 回扣问题 6] 　 (2017· 广州模拟 ) 如图 ① ，在平面四边形 ABCD 中，已知 ∠ A ＝ 45 °， ∠ C ＝ 90 °， ∠ ADC ＝ 105 °， AB ＝ BD ，现将四边形 ABCD 沿 BD 折起，使平面 ABD ⊥ 平面 BDC ( 如图 ② ) ，设点 E ， F 分别为棱 AC ， AD 的中点 . (1) 求证： DC ⊥ 平面 ABC ； (2) 设 CD ＝ a ，求三棱锥 A － BFE 的体积 . (1) 证明 　在题图 ① 中， AB ＝ BD ，且 ∠ A ＝ 45 °， ∴∠ ADB ＝ 45 °， ∠ ABD ＝ 90 °，则 AB ⊥ BD . 在题图 ② 中， ∵ 平面 ABD ⊥ 平面 BDC ，且平面 ABD ∩ 平面 BDC ＝ BD ， AB ⊂ 平面 ABD ， ∴ AB ⊥ 底面 BDC ，且 CD ⊂ 平面 BDC ， ∴ AB ⊥ CD . 又 ∠ DCB ＝ 90 °， ∴ DC ⊥ BC ，且 AB ∩ BC ＝ B ， ∴ DC ⊥ 平面 ABC .