高中数学选修2-2教学课件6_1_3演绎推理 31页

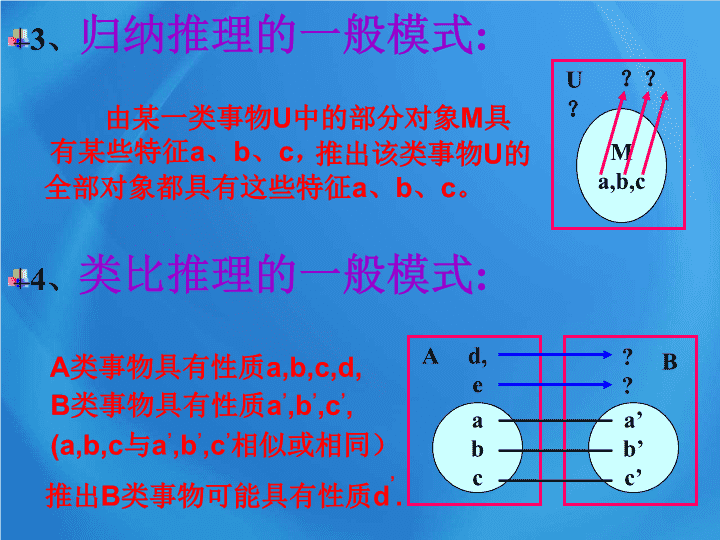
（ 1 ）、观察 1+3=4=2 2 , 1+3+5=9=3 2 , 1+3+5+7=16=4 2 , 1+3+5+7+9=25= , …… 由上述具体事实能得到怎样的结论？ （ 2 ）、在平面内，若 a⊥c,b⊥c, 则 a//b. 类比地推广到空间，你会得到 什么结论？并判断正误。 正确 错误 （可能相交） 1+3+……+(2n-1)=n 2 在空间中，若 α ⊥γ ， β ⊥γ 则 α//β 。 复习： 3 、 归纳推理的一般模式 : 4 、 类比推理的一般模式 : 推出 B 类事物可能具有性质 d ’ . A 类事物具有性质 a,b,c,d, B 类事物具有性质 a ’ ,b ’ ,c ’ , (a,b,c 与 a ’ ,b ’ ,c ’ 相似或相同） a b c a’ b’ c’ A B M a,b,c U ？？？ 由某一类事物 U 中的部分对象 M 具有某些特征 a 、 b 、 c ， ? ? d, e 推出该类事物 U 的全部对象都具有这些特征 a 、 b 、 c 。 学习目标： 1 、什么是演绎推理？ 2 、什么是三段论？ 3 、合情推理与演绎推理有哪些区别？ 4 、能举出一些在生活和学习中有关演绎 推理的例子。 三、新课 小明是一名高二年级的学生， 17 岁，迷恋上网络，沉迷于虚拟的世界当中。由于每月的零花钱不够用，便向亲戚要钱，但这仍然满足不了需求，于是就产生了歹念，强行向路人抢取钱财。但小明却说我是未成年人而且就抢了 50 元，这应该不会很严重吧？？？ 如果你是法官，你会如何判决呢？小明到底是不是犯罪呢？ 情景创设 1 ： 生活中的例子 1. 所有的金属都能导电 , 2. 一切奇数都不能被 2 整除 , 3. 三角函数都是周期函数 , 4. 全等的三角形面积相等 所以铜能够导电 . 因为铜是金属 , 所以 (2 100 +1) 不能被 2 整除 . 因为 (2 100 +1) 是奇数 , 因为 tan 三角函数 , 那么三角形 ABC 与三角形 A 1 B 1 C 1 面积相等 . 如果三角形 ABC 与三角形 A 1 B 1 C 1 全等 , 大前提 小前提 结论 大前提 小前提 结论 情景创设 2 ：观察下列推理 有什么特点？ 所以是 tan 周期函数 大前提 小前提 结论 结论 小前提 大前提 从一般性的原理出发，推出某个特殊情况下的结论，这种推理称为 演绎推理． 一、演绎推理的定义 : 二、演绎推理的模式 : “ 三段论 ” 是演绎推理的 一般 模式； M …… P （ M 是 P) S …… M (S 是 M) S …… P (S 是 P) 大前提 --- 已知的一般原理； 小前提 --- 所研究的特殊对象； 　　　 结论 --- 据一般原理，对特殊 对象做出的判断． M S P 若集合 M 的所有元素 都具有性质 P ， S 是 M 的一个子集，那么 S 中所有元素也都具有 性质 P 。 所有的金属 (M) 都能够导电 (P) 铜 (S) 是金属 (M) 铜 (S) 能够导电 (P) M …… P S …… M S …… P 用集合的观点来理解 : 三段论推理的依据 大前提： 刑法规定抢劫罪是以非法占有为目的，使用暴力、胁迫或其他方法，强行劫取公私财物的行为。其刑事责任年龄起点为 14 周岁，对财物的数额没有要求。 小前提： 小明超过 14 周岁，强行向路人抢取钱财 50 元。 结论： 小明犯了抢劫罪。 小明是一名高二年级的学生， 17 岁，迷恋上网络，沉迷于虚拟的世界当中。由于每月的零花钱不够用，便向亲戚要钱，但这仍然满足不了需求，于是就产生了歹念，强行向路人抢取钱财。但小明却说我是未成年人而且就抢了 50 元，这应该不会很严重吧？？ 三、演绎推理的特点 : 1 ．演绎推理的前提是一般性原理，演绎所得的的结论是蕴含于前提之中的个别、特殊事实，结论完全蕴含于前提之中，因此 演绎推理是由 一般到特殊 的推理； 2 、在演绎推理中，前提与结论之间存在着必然的联系， 只要前提和推理形式是正确的，结论必定正确 。因此 演绎推理是数学中严格的证明工具。 3 、在演绎推理是一种 收敛性 的思维方法，它 较少创造性 ，但却具有 条理清晰、令人信服 的论证作用，有助于科学论证和系统化。 四、合情推理与演绎推理的区别 区别 推理 形式 推理结论 联系 合情推理 归纳推理 类比推理 由 部分到整体、个 别到一般 的推理。 由 特殊到特殊 的 推理。 结论不一定正确，有待进一 步证明。 演绎推理 由 一般到特殊 的 推理。 在大前提、小前提 和推理形式都正确 的前提下，得到的 结论一定正确。 合情推理的结论需要演绎推理的验证，而演绎 推理的方向和思路一般是通过合情推理获得的。 大前提 小前提 结论 所有金属都能导电 铜 是金属 太阳系大行星以椭圆轨道绕太阳运行 冥王星 是太阳系的大行星 奇数都不能被 2 整除 2007 是奇数 2007 不能被 2 整除 冥王星以椭圆形轨道绕太阳运行 铜能导电 注 演绎推理有时可用列表的形式表示，如： 数学应用： 大前提 小前提 结论 大前提 小前提 结论 练习 1 下面说法正确的有（ ） （ 1 ）演绎推理是由一般到特殊的推理； （ 2 ）演绎推理得到的结论一定是正确的； （ 3 ）演绎推理一般模式是 “ 三段论 ” 形式； （ 4 ）演绎推理的结论的正误与大前提、小前提和推理形式有关。 A 、 1 个 B 、 2 个 C 、 3 个 D 、 4 个 C 例 2 ：用三段论的形式写出下列演绎推理。 （ 1 ）三角形内角和 180° ，等边三角形内角和是 180° 。 （ 1 ）分析：省略了 小前提 ：“等边三角形是三角形”。 （ 2 ） 是有理数。 （ 2 ）分析：省略了 大前提 ：“所有的循环小数都是有理数。” 小前提 ： 是循环小数。 解： 三角形内角和 180° ， 所以等边三角形内角和是 180° 。 等边三角形是三角形。 因为指数函数 是增函数， ········ 大前提 而 是指数函数， ····· ······ 小前提 所以 是增函数。 ············· 结论 （ 1 ）上面的推理形式正确吗？ （ 2 ）推理的结论正确吗？为什么？ 上述推理的形式是正确，但大前提是错误的（因为指数函数 y =a x (0BC,CD 是 AB 边上的高，求证∠ ACD ＞∠ BCD 。 A C D B 证明： 在△ ABC 中， 因为 CD⊥AB ， AC ＞ BC 所以 AD>BD, 于是∠ ACD ＞∠ BCD 。 错因：偷换概念 如图，在 △ ABC 中， AC > BC , CD 是 AB 上的高， 求证： ∠ ACD > ∠BCD. 证明： 在△ ABC 中，因为 , AC > BC, 所以 AD > BD ， 于是∠ ACD > ∠BCD. 指出上面证明过程中的错误。 根据 AD > BD ，不能推出∠ ACD > ∠BCD. 因为在同一个三角形中，才有大边对大角， AD 和 BD 不是同一 个三角形的边。 正确的证法： 在△ ABC 中， ∵ AC > BC ，∴ ∠ B > ∠A (2) 在演绎推理中，只要前提和推理形式是正确的，结论必定正确。 练习 2 下列几种推理过程是演绎推理的是（ ） A 、 5 和 可以比较大小； B 、由平面三角形的性质，推测空间四面体的性质； C 、东升高中高二级有 15 个班， 1 班有 51 人， 2 班有 53 人， 3 班有 52 人，由此推测各班都超过 50 人； D 、预测股票走势图。 A 例 3: 证明函数 f ( x )=- x 2 +2 x 在 (- ∞ ,1] 上是增函数 . 满足对于任意 x 1 , x 2 ∈ D, 若 x 1 < x 2 , 有 f ( x 1 )< f ( x 2 ) 成立的函数 f ( x ), 是区间 D 上的增函数 . 任取 x 1 , x 2 ∈(- ∞,1] 且 x 1 0 ， 因为 x 1 , x 2 ≤ 1 所以 x 1 + x 2 -2 < 0 ， 因此 f ( x 1 )- f ( x 2 )<0, 即 f ( x 1 ) 0, 所以 mb0, ( 大前提） ( 小前提） ( 大前提） ( 小前提） ( 大前提） ( 小前提） ( 结论） ( 结论） ( 结论） 演绎推理 概念 一般形式 —— 三段论 证明问题 合情推理与演绎推理的联系与区别 （难点） （重点） （重点） 四、小结 对于任意正整数 n ，猜想（ 2n-1) 与（ n+1) 2 的大小关系。并用演绎推理证明你的结论。 思考题： 在数列 {a n } 中， 试猜想这个数列的通项公式； 并用演绎推理证明你的猜想。 思考题： 《 　　 》