2019学年高二数学下学期4月月考试题 文新人教版 新版 8页

北重三中2019年-2019学年度第二学期高二年级月考考试文科数学试题 考试时间：2019年4月7日 满分：150分 考试时长：120分钟 第一部分 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1. 复数的值是 （ ）‎ ‎ A．－2i B．2i C．2 D．-2‎ ‎2. 下列各命题中是真命题的为 （ ）‎ A．如果，那么 B．如果，那么 C．如果，那么 D．如果，， 那么 ‎ ‎3. 已知函数的导数为，则 ( )‎ ‎ A. B.‎ C. D.‎ ‎4．下面是关于复数的四个命题：‎ ‎， ， 的共轭复数为， 的虚部为.其中的真命题为 （ ）‎ A. B. C. D. ‎ ‎5．某样本数据如下表: 由该样本数据得到的回归方程为＝x＋.若＝7.9，则的值为 (　 )‎ 8‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ y ‎4.0‎ ‎2.5‎ ‎－0.5‎ ‎0.5‎ ‎－2.0‎ A．1.4 B．－1.4 C．1.2 D. －1.2‎ ‎6. 如图，在复平面内，复数，对应的向量分别是，，则复数对应的点位于 （ ）‎ A. 第一象限 B. 第二象限 ‎ ‎ C. 第三象限 D. 第四象限 ‎7. 二次函数y=f(x)的图象过原点,且它的导数y=f′(x)的图象是如图所示的一条直线,则函数y=f(x)的图象的顶点在 (　 ) ‎ ‎ A第一象限 B第二象限 C第三象限 D第四象限 ‎8. 已知在上是单调增函数，则的最大值 （ ）‎ A.0 B.1 C.2 D.3‎ ‎9. 等比数列中，公比首项，函数，则= （ ）‎ A．8 B．-8 C． D．- ‎ ‎10. 已知函数（m为常数）在上有最大值3，那么此函数在上的最小值为 （ ）‎ A.-3 B.-37 C.-28 D.-13‎ ‎11. 已知二次函数的导数为，，对于任意实数都有，则 的最小值为 ( )‎ A． B． C． D．‎ 8‎ 第二部分 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13. 若 z1=a+2i, z2=3-4i，且为纯虚数，则实数a的值为 ；‎ ‎14.若，则函数的最大值为 ；‎ ‎15.已知函数是上的奇函数，且在上有，若，那么关于的不等式的解集是 ；‎ ‎16. 已知点在曲线上，为曲线在点处的切线的倾斜角，则的取值范围是 。‎ 三、简答题：本大题共6个小题，第一小题10分，其余每小题各12分.‎ ‎17．（本小题满分10分）已知点P在函数的图像上.‎ ‎（Ⅰ）求曲线在点P（1,f(1）)处的切线方程； ‎ ‎（II）求函数的单调区间和极值. 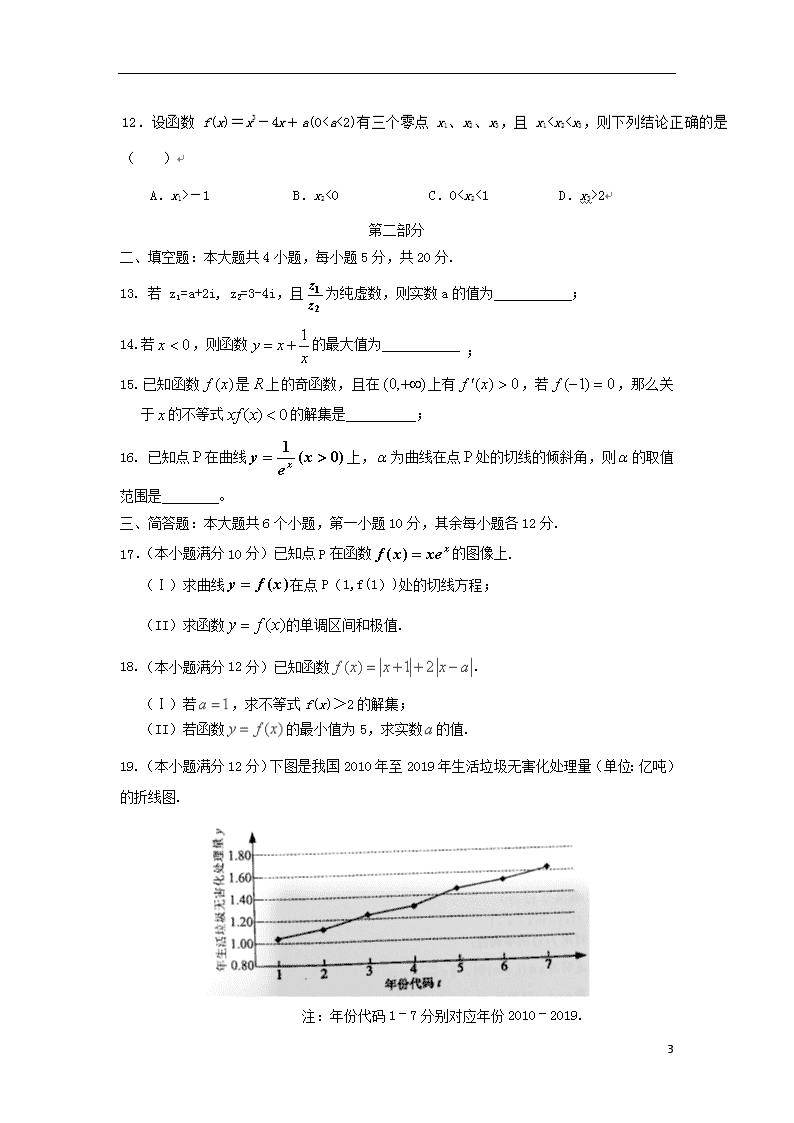‎ ‎18.（本小题满分12分）已知函数.‎ ‎（Ⅰ）若，求不等式f(x)＞2的解集；‎ ‎（II）若函数的最小值为5，求实数的值.‎ ‎19.（本小题满分12分）下图是我国2010年至2019年生活垃圾无害化处理量（单位：亿吨）的折线图.‎ 注：年份代码1–7分别对应年份2010–2019.‎ 8‎ ‎（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；‎ ‎（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2019年我国生活垃圾无害化处理量.‎ 附注：参考数据：，，，≈2.646.‎ 参考公式：‎ 回归方程中斜率和截距的最小二乘估计公式分别为：‎ ‎ , ‎ ‎20．（本小题满分12分）为了调查某大学学生在周日上网的时间，随机对100名男生和100名女生进行了不记名的问卷调查，得到了如下的统计结果：‎ 表1：男生上网时间与频数分布表 上网时间(分钟)‎ ‎[30,40)‎ ‎[40,50)‎ ‎[50,60)‎ ‎[60,70)‎ 人数 ‎5‎ ‎25‎ ‎30‎ ‎25‎ ‎15‎ 表2：女生上网时间与频数分布表 上网时间(分钟)‎ ‎[30,40)‎ ‎[40,50)‎ ‎[50,60)‎ ‎[60,70)‎ 人数 ‎10‎ ‎20‎ ‎40‎ ‎20‎ ‎10‎ ‎(Ⅰ)若该大学共有女生750人，试估计其中上网时间不少于60分钟的人数；‎ ‎(II)完成下面的2×2列联表，并回答能否有90%的把握认为“大学生周日上网时间与性别有关”？‎ 表3：‎ 上网时间少于60分钟 上网时间不少于60分钟 合计 男生 女生 合计 附：K2＝ 8‎ P(K2≥k0)‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ k0‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ P(K2≥k0)‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎3.84‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.83‎ ‎21．（本小题满分12分）已知函数，且.‎ ‎(Ⅰ)求的值；‎ ‎(II)设函数，若函数g(x)在x∈上单调递增，求实数c的取值范围．‎ ‎22.（本小题满分12分）已知函数．‎ ‎（Ⅰ）求函数的单调递减区间；‎ ‎（II）若在上恒成立，求实数的取值范围； ‎ ‎（III）过点作函数图像的切线，求切线方程．‎ 北重三中2019年-2019学年度第二学期 高二年级月考考试文科数学试题答案 考试时间：2019年4月7日 满分：150分 考试时长：120分钟 ‎ ‎ 第一部分 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1-12. C D A C B B C D A B C C ‎ 8‎ ‎13. ； 14.-2 ； 14.；15.。‎ 三、简答题：本大题共6个小题，第一小题10分，其余每小题各12分.‎ ‎17.（Ⅰ）y=2ex-e ‎ ‎（II）f(x)的递减区间，递增区间, 极小值为,无极大值.‎ ‎18．（Ⅰ）‎ ‎（II） 或 ‎19. 解：（Ⅰ）由折线图中数据和附注中参考数据得 ‎，，，‎ ‎，‎ ‎. ........4分 因为与的相关系数近似为0.99，说明与的线性相关程度相当高，从而可以用线性回归模型拟合与的关系. ............6分 ‎（Ⅱ）由及（Ⅰ）得，‎ ‎.‎ 所以，关于的回归方程为：. ..........10分 将2019年对应的代入回归方程得：.‎ 所以预测2019年我国生活垃圾无害化处理量将约1.82亿吨. .........12分 ‎20．(1)设估计上网时间不少于60分钟的人数为x，‎ 依题意有＝，解得x＝225，‎ 所以估计其中上网时间不少于60分钟的人数是225.‎ ‎(2)根据题目所给数据得到如下列联表：‎ 上网时间少于60分钟 上网时间不少于60分钟 合计 8‎ 男生 ‎60‎ ‎40‎ ‎100‎ 女生 ‎70‎ ‎30‎ ‎100‎ 合计 ‎130‎ ‎70‎ ‎200‎ 其中K2＝＝≈2.198＜2.706，‎ 因此，没有90%的把握认为“大学生周日上网时间与性别有关”．‎ ‎21.解:(1)由f(x)＝x3＋ax2－x＋c，‎ 得f′(x)＝3x2＋2ax－1.‎ 当x＝时，得a＝f′＝3×2＋2f′×－1，解之，得a＝－1.‎ ‎ (2)函数g(x)＝·ex＝(－x2－x＋c)·ex，‎ 有g′(x)＝(－2x－1)ex＋(－x2－x＋c)ex＝(－x2－3x＋c－1)ex.因为函数在区间x∈上单调递增，等价于h(x)＝－x2－3x＋c－1≥0在x∈上恒成立，由于函数h(x)的图象的对称轴方程是x＝－，因此只要h(2)≥0，解得c≥11，所以c的取值范围是c≥11.‎ ‎22、解：（Ⅰ）得 ‎ ‎ 函数的单调递减区间是；………………4分 ‎ （Ⅱ）即 ‎ 设则………………2分 ‎ 当时，函数单调递减；‎ ‎ 当时，函数单调递增；‎ ‎ 最小值实数的取值范围是；………………8分 ‎（Ⅲ）设切点则即 ‎ 设，当时是单调递增函数 ………………10分 最多只有一个根，又 ‎ 由得切线方程是. ………………12分 8‎ 8‎