2018届二轮复习二项式定理在数列求和中的应用学案（全国通用） 4页

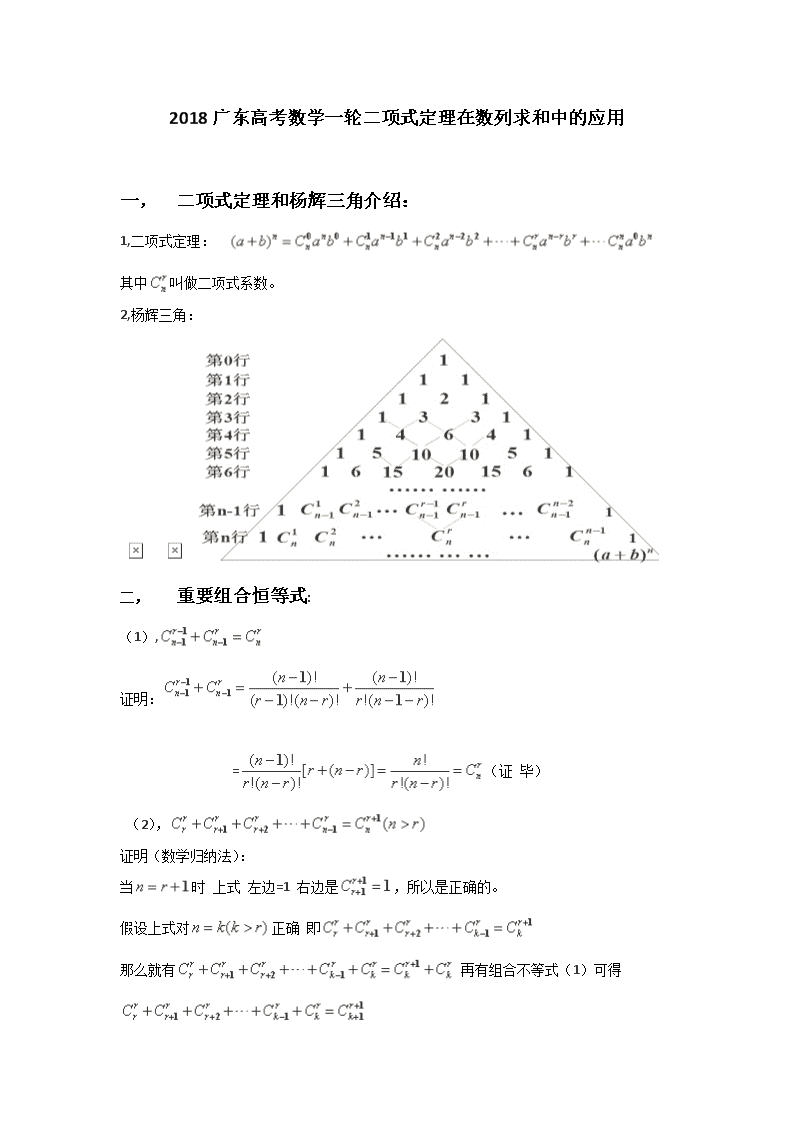
‎2018广东高考数学一轮二项式定理在数列求和中的应用 ‎ ‎ 一， 二项式定理和杨辉三角介绍：‎ ‎1,二项式定理： ‎ 其中叫做二项式系数。‎ ‎2,杨辉三角：‎ ‎ ‎ 二， 重要组合恒等式:‎ ‎（1）,‎ 证明：‎ ‎ =（证 毕）‎ ‎ （2），‎ 证明（数学归纳法）：‎ 当时 上式 左边=1 右边是，所以是正确的。‎ 假设上式对正确 即 ‎ 那么就有 再有组合不等式（1）可得 故综上所述 对于所有大于r的正整数n（2）式都是成立的。‎ 三， 一元n次多项式根与系数的关系 对于多项式 若是它的n个根则有一下等式成立：‎ ‎（所有i个不同的根的乘积的和）‎ 四， 应用举例 为了方便应用，（2）式也可以写成 当r=1，2，3，4的时候上式也就是：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 例一：求数列 的前n项和。‎ 分析：因为 所以 ‎=‎ 例二：求数列的前n项和。‎ 分析：因为 所以 例三：求数列的前n项和。‎ 分析：因为 所以：=‎ ‎=‎ 四， 归纳总结 推论 若多项式他的根分别是，则 他的展开式中的系数是 同理展开式中的系数是：‎ 规律总结：求数列的方法 步骤一：分拆通项 ‎++‎ 步骤二：利用组合不等式（2）分组求和就可求出前n项和。‎