高考数学复习课时提能演练(十五) 2_12 9页

‎ ‎ 课时提能演练(十五)‎ ‎(45分钟 100分)‎ 一、选择题(每小题6分，共36分)‎ ‎1. 1.（2012·厦门模拟）已知a,b,c,d成等差数列，函数y=ln(x+2)-x在x=b处取得极大值c,则b+d=（ ）‎ ‎(A)-1 (B)0 (C)1 (D)2‎ ‎2.对于R上可导的任意函数f(x)，若满足(x-1)f′(x)≥0，则必有( )‎ ‎(A)f(0)+f(2)＜‎2f(1)‎ ‎(B)f(0)+f(2)≤‎2f(1)‎ ‎(C)f(0)+f(2)≥‎2f(1)‎ ‎(D)f(0)+f(2)＞‎2f(1)‎ ‎3.(2011·辽宁高考)函数f(x)的定义域为R，f(-1)=2，对任意x∈R，‎ f′(x)＞2，则f(x)＞2x+4的解集为( )‎ ‎(A)(-1，1) (B)(-1，+∞)‎ ‎(C)(-∞，-1) (D)(-∞，+∞)‎ ‎4.已知函数f(x)=x3+bx2+cx+d在区间[-1,2]上是减函数，那么b+c( )‎ ‎(A)有最大值 (B)有最大值-‎ ‎(C)有最小值 (D)有最小值-‎ ‎5.函数f(x)= ex(sinx+cosx)在区间[0，]上的值域为( )‎ ‎(A)[，] (B)(，)‎ ‎(C)[1，] (D)(1，)‎ ‎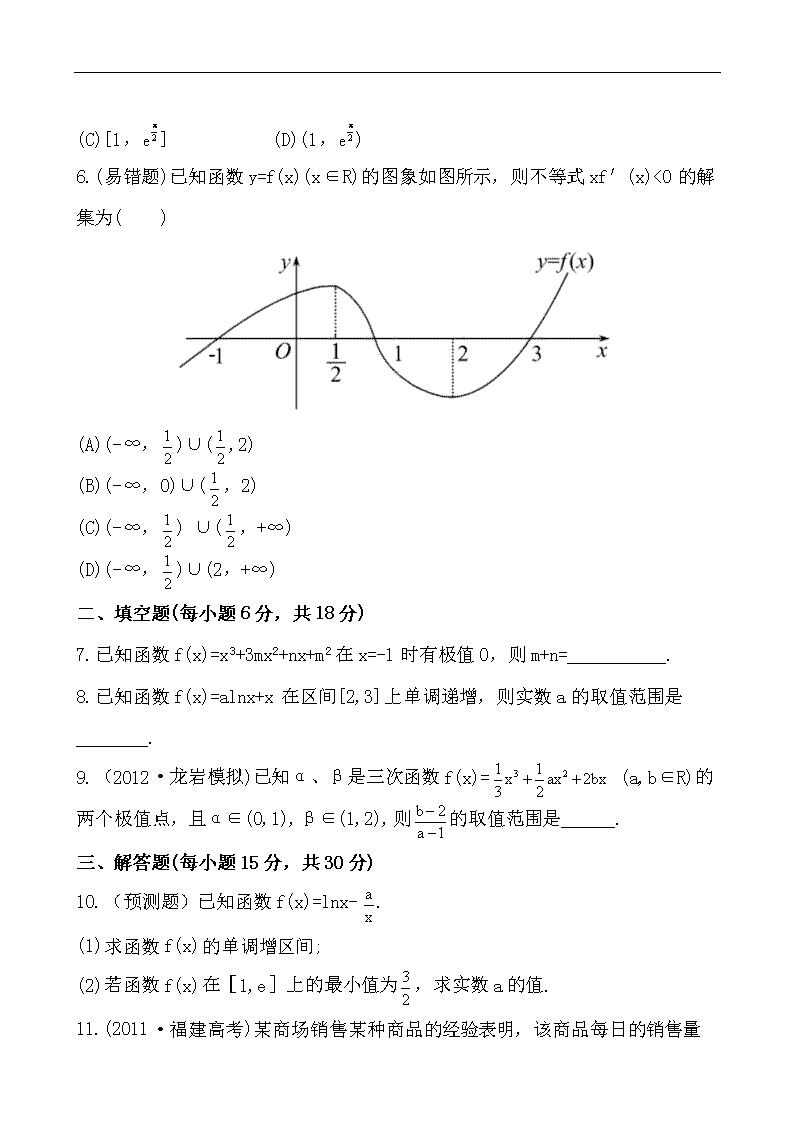6.(易错题)已知函数y=f(x)(x∈R)的图象如图所示，则不等式xf′(x)<0的解集为( )‎ ‎(A)(-∞，)∪(,2)‎ ‎(B)(-∞，0)∪(，2)‎ ‎(C)(-∞，) ∪(，+∞)‎ ‎(D)(-∞，)∪(2，+∞)‎ 二、填空题(每小题6分，共18分)‎ ‎7.已知函数f(x)=x3+3mx2+nx+m2在x=-1时有极值0，则m+n=___________.‎ ‎8.已知函数f(x)=alnx+x在区间[2,3]上单调递增，则实数a的取值范围是________.‎ ‎9.（2012·龙岩模拟)已知α、β是三次函数f(x)= (a,b∈R)的两个极值点，且α∈(0,1),β∈(1,2),则的取值范围是______.‎ 三、解答题(每小题15分，共30分)‎ ‎10.（预测题）已知函数f(x)=lnx-.‎ ‎(1)求函数f(x)的单调增区间;‎ ‎(2)若函数f(x)在［1,e］上的最小值为，求实数a的值.‎ ‎11.(2011·福建高考)‎ 某商场销售某种商品的经验表明，该商品每日的销售量y(单位：千克)与销售价格x(单位：元/千克)满足关系式y= +10(x-6)2，其中3＜x＜6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克.‎ ‎(1)求a的值；‎ ‎(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.‎ ‎【探究创新】‎ ‎(16分)某造船公司年最大造船量是20艘，已知造船x艘的产值函数为R(x)=‎ ‎3 700x+45x2-10x3(单位：万元)，成本函数为C(x)=460x+5 000(单位：万元)，又在经济学中，函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).‎ ‎(1)求利润函数P(x)及边际利润函数MP(x)；(提示：利润=产值-成本)‎ ‎(2)问年造船量安排多少艘时，可使公司造船的年利润最大？‎ ‎(3)求边际利润函数MP(x)的单调递减区间，并说明单调递减在本题中的实际意义是什么？‎ 答案解析 ‎1.【解析】选D.y′=,令y′=0，得x=-1,‎ 即b=-1,c=ln1-(-1)=1,‎ 又a,b,c,d成等差数列，‎ ‎∴d=b+2(c-b)=3,‎ ‎∴b+d=-1+3=2.‎ ‎2.【解题指南】分x>1和x＜1两种情况讨论单调性.‎ ‎【解析】选C.当x>1时，f′(x)≥0,‎ 若f′(x)=0,则f(x)为常数函数，‎ 若f′(x)>0，则f(x)为增函数,总有f(x)≥f(1).‎ 当x<1时，f′(x)≤0,若f′(x)=0，则f(x)为常数函数.‎ 若f′(x)<0,则f(x)为减函数，总有f(x)≥f(1),‎ ‎∴f(x)在x=1处取得最小值.‎ 即f(0)≥f(1),f(2)≥f(1),∴f(0)+f(2)≥‎2f(1).‎ ‎3.【解题指南】构造函数g(x)=f(x)-(2x+4)，判断其单调性，求解.‎ ‎【解析】选B.由已知，[f(x)-(2x+4)]′=f′(x)-2＞0，‎ ‎∴g(x)=f(x)-(2x+4)单调递增，‎ 又g(-1)=0，∴f(x)＞2x+4的解集是(-1，+∞).‎ ‎4.【解析】选B.由f(x)在[-1,2]上是减函数，知 f′(x)=3x2+2bx+c≤0，x∈[-1,2]，‎ 则⇒‎ ‎15+2b+‎2c≤0⇒b+c≤-.‎ ‎5.【解析】选A.f′(x)=ex(sinx+cosx)+ex(cosx-sinx)=excosx，‎ 当00,‎ ‎∴f(x)是[0，]上的增函数.‎ ‎∴f(x)的最大值为f()=，‎ f(x)的最小值为f(0)= .‎ ‎∴f(x)的值域为[,].‎ ‎6.【解析】选B.由f(x)图象的单调性可得f′(x)在(-∞，)和(2，+∞)上大于0，在(，2)上小于0，‎ ‎∴xf′(x)<0的解集为(-∞，0)∪(，2).‎ ‎7.【解析】∵f′(x)=3x2+6mx+n,‎ ‎∴由已知可得∴或,‎ 当时，f′(x)=3x2+6x+3=3(x+1)2≥0恒成立与x=-1是极值点矛盾，‎ 当时，f′(x)=3x2+12x+9=3(x+1)(x+3),‎ 显然x=-1是极值点，符合题意，‎ ‎∴m+n=11.‎ 答案：11‎ ‎【误区警示】本题易出现求得m,n后不检验的错误.‎ ‎8.【解析】∵f(x)=alnx+x，∴f′(x)=+1.‎ 又∵f(x)在[2,3]上单调递增，‎ ‎∴+1≥0在x∈[2,3]上恒成立，‎ ‎∴a≥(-x)max=-2，∴a∈[-2，+∞).‎ 答案：[-2，+∞)‎ ‎9.【解析】f′(x)=x2+ax+2b,由题意知，方程f′(x)=0有两根α、β，一根 α∈(0,1),另一根β∈(1,2),‎ ‎∴‎ 设结合线性规划得z的取值范围为(,1).‎ 答案：(,1)‎ ‎10.【解析】(1)f(x)的定义域为(0,+∞),且f′(x)= .‎ a≥0时，f′(x)＞0,∴f(x)的单调增区间为(0,+∞),‎ a＜0时，令f′(x)＞0,得x＞-a,∴f(x)的单调增区间为(-a,+∞).‎ ‎(2)由(1)可知，f′(x)= ,‎ ‎①若a≥-1,则x+a≥0,即f′(x)≥0在［1,e］上恒成立，f(x)在［1,e］上为增函数，∴f(x)min=f(1)=-a=,∴a=-(舍去).‎ ‎②若a≤-e,则x+a≤0，即f′(x)≤0在［1,e］上恒成立，f(x)在［1,e］上为减函数，∴f(x)min=f(e)=1-=,∴a=-(舍去).‎ ‎③若-e＜a＜-1,当1＜x＜-a时，f′(x)＜0,‎ ‎∴f(x)在(1,-a)上为减函数，‎ 当-a＜x＜e时，f′(x)＞0,∴f(x)在(-a,e)上为增函数.‎ ‎∴f(x)min=f(-a)=ln(-a)+1=,∴a=-,‎ 综上所述，a=-.‎ ‎【变式备选】已知函数f(x)=+alnx-2(a＞0).‎ ‎(1)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直，求函数y=f(x)的单调区间;‎ ‎(2)若对于任意的x∈(0,+∞)，都有f(x)＞2(a-1)成立，试求实数a的取值范围;‎ ‎(3)记g(x)=f(x)+x-b(b∈R).当a=1时，方程g(x)=0在区间［e-1,e］上有两个不同的实根，求实数b的取值范围.‎ ‎【解析】(1)函数f(x)的定义域为(0,+∞).‎ 因为f′(x)=-，且知直线y=x+2的斜率为1.‎ 所以f′(1)=- =-1,所以a=1.‎ 所以f(x)=+lnx-2.f′(x)= .‎ 由f′(x)＞0,解得x＞2;由f′(x)＜0解得0＜x＜2.‎ 所以f(x)的单调增区间是(2,+∞)，单调减区间是(0,2).‎ ‎(2)f′(x)=- .‎ 由f′(x)＞0解得x＞;由f′(x)＜0解得0＜x＜.‎ 所以f(x)在区间(,+∞)上单调递增，在区间(0, )上单调递减.‎ 所以当x=时，函数f(x)取得最小值，ymin=f().‎ 因为对任意的x∈(0,+∞)都有f(x)＞2(a-1)成立，‎ 所以f()＞2(a-1)即可.则 +aln-2＞2(a-1)，即aln＞a,解得0＜a＜.‎ 所以a的取值范围是(0, ).‎ ‎(3)依题意得g(x)= +lnx+x-2-b,则g′(x)= .‎ 由g′(x)＞0解得x＞1;由g′(x)＜0解得0＜x＜1.‎ 所以函数g(x)在区间(0,1)上为减函数，在区间(1,+∞)上为增函数.‎ 又因为方程g(x)=0在区间［e-1,e］上有两个不同的实根，所以 解得1＜b≤+e-1.‎ 所以b的取值范围是(1,+e-1］.‎ ‎11.【解析】(1)因为x=5时y=11，‎ 所以+10=11,所以a=2；‎ ‎(2)由(1)知该商品每日的销售量y=+10(x-6)2，‎ 所以商场每日销售该商品所获得的利润：‎ f(x)=(x-3)[+10(x-6)2]=2+10(x-3)(x-6)2,3＜x＜6；‎ 从而f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6)，令f′(x)=0得x=4,‎ 函数f(x)在(3,4)上单调递增，在(4,6)上单调递减，所以当x=4时函数f(x)取得最大值f(4)=42.‎ 答：当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.‎ ‎【探究创新】‎ ‎【解析】(1)P(x)=R(x)-C(x)=-10x3+45x2+3 240x-5 000(x∈N*，且1≤x≤20);‎ MP(x)=P(x+1)-P(x)‎ ‎=-30x2+60x+3 275 (x∈N*,且1≤x≤19).‎ ‎(2)P′(x)=-30x2+90x+3 240‎ ‎=-30(x-12)(x+9),‎ ‎∵x>0,∴P′(x)=0时,x=12，‎ 当00,‎ 当x>12时，P′(x)<0,‎ ‎∴x=12时，P(x)有极大值，也是最大值.‎ 即年造船量安排12艘时，可使公司造船的年利润最大.‎ ‎(3)MP(x)=-30x2+60x+3 275=-30(x-1)2+3 305.‎ 所以，当x≥1时，MP(x)单调递减，‎ 所以单调减区间为［1，19］，且x∈N*.‎ MP(x)是减函数的实际意义是：随着产量的增加，每艘利润与前一艘比较，利润在减少.‎