河南省陕州中学2019-2020学年高一下学期期末考试数学试题 9页

郑州市2019—2020学年下期期末考试 高中一年级数学 第Ⅰ卷（选择题，共60分）‎ 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．已知平行四边形ABCD中，向量，，则向量 A． （1，5）‎ B． (-2，7) ‎ C． (5，4)‎ D． （1，10）‎ ‎2．sin的值等于 ‎3．某学校从编号依饮为01，02，… ，72的72个学生中用系统抽样（等间距抽样）的方法抽取一个样本，已知样本中相邻的两个组的编号分别为12，21，则该样本中来自第四组的学生的编号为 A． 30‎ B． 31‎ C．32‎ D． 33‎ ‎4．下列函数中是偶函数且最小正周期为的是 ‎5．已知某7个数据的平均数为5，方差为4，现又加入一个新数据5，此时这8个数的方差为 A． B． 3‎ C． D． 4‎ ‎6．已知，且，则 A．-7 B．7‎ ‎7．设a是一个各位数字都不是0且没有重复数字的两位数．将组成a的2个数字按从小到大排成的两位数记为I（a），按从大到小排成的两位数记为D（a）（例如a=75，则I（a）=57， D（a）=75），执行如图所示的程序框图，若输入的a=97，则输出的b=‎ A．45‎ B． 40 ‎ C．35‎ D． 30‎ ‎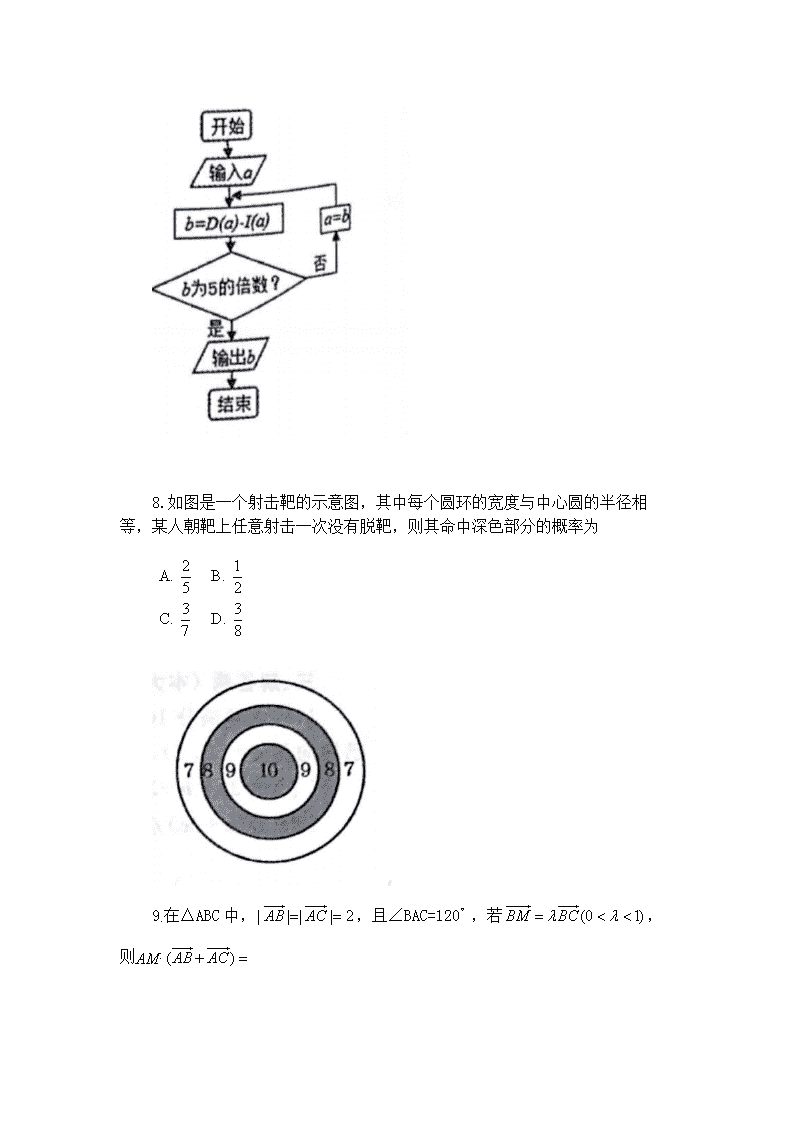8.如图是一个射击靶的示意图，其中每个圆环的宽度与中心圆的半径相等，某人朝靶上任意射击一次没有脱靶，则其命中深色部分的概率为 ‎9.在△ABC中，，且∠BAC=120°，若，则× ‎ A．2 B．1 C. D. ‎ ‎ ‎ ‎10.若点在函数的图象上，为了得到函数y=sin（2x+）（x∈R）的图象，只需把曲线f（x）上所有的点 A．向左平行移动个单位长度 B．向右平行移动个单位长度打 C．向右平行移动个单位长度 D．向左平行移动个单位长度 ‎11.已知与a—b的夹角为，则 ‎ A．2‎ В．3‎ C． 4‎ D．5‎ ‎12．若关于x的方程有两个不同的解，则实数a的取值范围为 第Ⅱ卷（共90分）‎ 二、填空题（每小题5分，共20分）‎ ‎13．已知向量，则________‎ ‎14.已知函数部分图象如图所示，则φ的值为________‎ ‎15.已知，则-x）的值________‎ ‎16.在Rt△ABC中，．以C为圆心，2为半径作圆，线段PQ为该圆的一条直径，则的最小值为________‎ 三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．）‎ ‎17. （本题满分10分）‎ 已知向量.‎ ‎（Ⅰ）求 ;‎ ‎(Ⅱ)若，求实数k．‎ ‎18． （本题满分12分）‎ 疫情期间口罩需求量大增，某医疗器械公司开始生产KN95口罩，并且对所生产口罩的质量按指标测试分数进行划分，其中分数不小于70的为合格品，否则为不合格品，现随机抽取100件口罩进行检测，其结果如下：‎ ‎（I）根据表中数据，估计该公司生产口罩的不合格率；‎ ‎（Ⅱ）根据表中数据，估计该公司口罩的平均测试分数；‎ ‎（Ⅲ）若用分层抽样的方式按是否合格从所生产口罩中抽取5件，再从这5件口罩中随机抽取2件，求这2件口罩全是合格品的概率．‎ ‎19． （本题满分12分）‎ 已知α，β为锐角，。‎ ‎(1)求cos2α的值；‎ ‎(2)求tan(β-α)的值.‎ ‎20．（本题满分12分）‎ 已知函数，其中 ‎ ‎(I)求函数f(x)的单调递增区间；‎ ‎（Ⅱ）求函数f（x）的最大值和最小值.‎ ‎21.（本题满分12分）如图，四边形OQRP为矩形，其中P，Q分别是函数图象上的一个最高点和最低点，O为坐标原点，R为图象与x轴的交点．‎ 求f（x）的解析式．‎ ‎22． （本题满分12分）‎ 红外线治疗仪的治疗作用是在红外线照射下，组织温度升高，毛细血管扩张，血流加快，物质代谢增强，组织细胞活力及再生能力提高，对我们身体某些疾病的治疗有着很大的贡献，某药店兼营某种红外线治疗仪，经过近5个月的营销，对销售状况进行相关数据分析，发现月销售量与销售价格有关，其统计数据如下表：‎ ‎（I）根据表中数据求y关于x的线性回归方程；‎ ‎（Ⅱ）①每台红外线治疗仪的价格为165元时，预测红外线治疗仪的月销售量；（四舍五入为整数）‎ ‎②若该红外线治疗仪的成本为120元/台，药店为使每月获得最大的纯收益，利用（Ⅰ）中结论，问每台该种红外线治疗仪的销售价格应定为多少元？ （四舍五人，精确到1元）．参考公式：回归直线方程，‎ 郑州市2019—2020学年下期期末考试评分参考 高中一年级数学 一、选择题 ‎1.D；2.A；3.A；4.A；5.C；6.D；7.A；8.D；9.A；10.D；11.B；12.D.‎ 二、填空题 ‎13.；14.；15． 16.-10.‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.解：（1）‎ ‎ ············4分 ‎（2），‎ ‎∵，∴‎ 解之得：············10分 ‎18.解：（1）在抽取的100件产品中，不合格的口罩有：4+16＝20（件）‎ 所以口罩为不合格品的频率为，‎ 根据频率可估计该公司所生产口罩的不合格率为． ············2分 ‎（2）平均测试分数为 ‎· ···········6分 ‎（3）由题意所抽取的5件口罩中不合格的1件，合格的4件．‎ 设4件合格口罩记为a，b，c，d，1件不合格口罩记为x.‎ 若抽取的口罩中恰有1件不合格，则共有ax, bx, cx, dx，4种情况. ···········8分 而从5件口罩中抽取2件，共有ab, ac, ad, ax, bc, bd, bx, cd, cx, dx，种情况.············10分 所以2件口罩中至少有一件不合格品的概率为.‎ 故2件口罩全是合格品的概率为. ············12分 ‎19.解：（1）由，得·············4分 ‎（2）由α，β为锐角，得α+β∈（0，π），2α∈（0，π），‎ 又cos（α+β），∴sin（α+β）, ·············4分 由，得． ·············10分 则 ·············12分 ‎20.（1） ‎ ‎············2分 ‎·············5分 ‎（2）∵，可得 ‎∴············8分 当时，函数有最大值-1；············10分 当时，函数有最小值.············12分 ‎21.解：设函数的最小正周期为T，则......2分 ‎ 因为四边形OQRP为矩形，得,所以 ...4分 ‎ 即,解得 ...8分 ‎ 所以. ...10分 ‎ 所以. ...12分 ‎22.解：，，············2分 ‎..‎ ‎，············4分 ‎，‎ 关于x的回归方程为．···········6分 由知，当时，，‎ 答：每台红外线治疗仪的价格为165元时，红外线治疗仪的月销量为40台.···········8分 药店每月获取得纯利. 所以当时，取得最大值. 答：药店为使每月获得最大的纯收益，每台该种红外线治疗仪的销售价格应定为163元．············12分