高中数学选修2-1课件2_1_3直线与椭圆的位置关系 18页

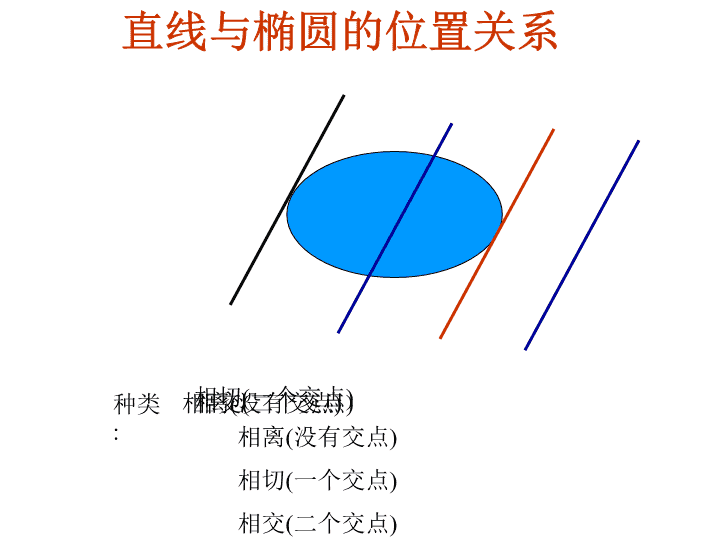
直线与椭圆的位置关系 直线与椭圆的位置关系 种类 : 相离 ( 没有交点 ) 相切 ( 一个交点 ) 相交 ( 二个交点 ) 相离 ( 没有交点 ) 相切 ( 一个交点 ) 相交 ( 二个交点 ) 直线与椭圆的位置关系的判定 mx 2 +nx+p=0 （ m≠ 0 ） Ax+By+C=0 由方程组： <0 方程组无解 相离 无交点 =0 方程组有一解 相切 一个交点 >0 相交 方程组有两解 两个交点 代数方法 = n 2 -4mp 例 1 ：直线 y=kx+1 与椭圆 恒有公共点 , 求 m 的取值范围。 （ 2012 年南昌市模拟考试） x y O B A 一元二次方程： 求根公式： 韦达定理： 直线与椭圆关系： 根的判别式： 弦长公式： 中点坐标计算公式： l m m 设弦的两个端点坐标分别为　　　　　　 ，代入圆锥 曲线得两方程后相减，得到弦中点坐标与弦所在直线斜率的关系，然后加以求解，这即为“ 点差法 ”， x y O M B A 例 5 中心在原点、一个焦点为 F( ,0) 的椭圆被直线 x-2y-2=0 截得的弦的中点的横坐标为 1 ，求此椭圆的方程 . 点差法步骤： 1. 设点 A( x 1 , y 1 ),B( x 2 , y 2 ); 2. 代入圆锥曲线方程作差 ; 3. 利用平方差公式变形，把中点坐标与直线斜率代入得到式子 . 点差法用途： 可以解决与中点弦有关的 一切 问题 . 变式 2: 已知直线 l 过点 M (1,0.5), 且与椭圆 x 2 +4y 2 =4 相交于 E,F 两点，求弦 EF 的中点的轨迹方程 . x y O l M E F 变式 1: 已知直线 l 过点 (1,0.5), 且与椭圆　　　　　相交于 E,F 两点，若 EF 的中点为 M ，求直线 l 的方程 . 思考 《 教材完全解读 》 经典例题： ２、弦长公式： 设直线 l 与椭圆 C 相交于 A( x 1 ， y 1 ) ， B( x 2 ， y 2 ) ， 则 |AB| ＝　 , 其中 k 是直线的斜率 １、判断直线与椭圆位置关系的方法： 解方程组消去其中一元得一元二次型方程 △< 0 相离 △= 0 相切 △> 0 相交 ３、处理 弦中点问题：“点差法”、“韦达定理” 小结 作业： 已知椭圆 5x 2 +9y 2 =45 ，椭圆的右焦点为 F ， (1) 求过点 F 且斜率为 1 的直线被椭圆截得的弦长 . (2) 判断点 A(1,1) 与椭圆的位置关系 , 并求以 A 为中点 椭圆的弦所在的直线方程 .