2018届二轮复习专题七第2讲　不等式选讲(选修4－5)课件（全国通用） 28页

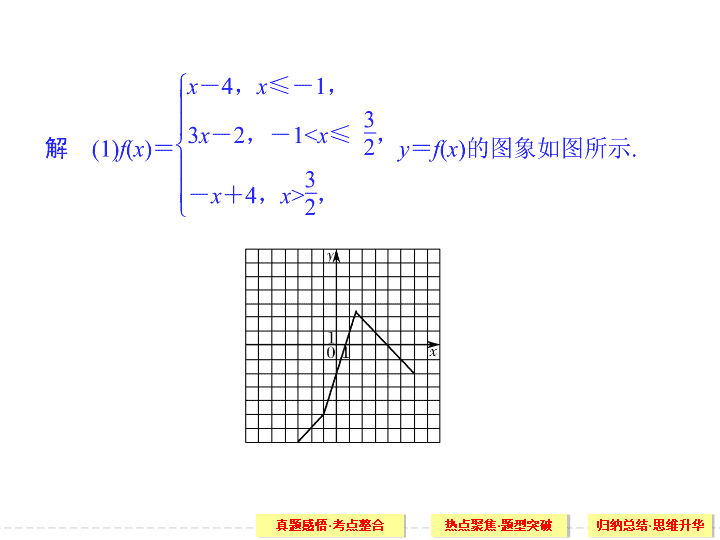
第 2 讲　不等式选讲 ( 选修 4 － 5) 高考定位　 本部分主要考查绝对值不等式的解法 . 求含绝对值的函数的值域及求含参数的绝对值不等式中的参数的取值范围，不等式的证明等，结合集合的运算、函数的图象和性质、恒成立问题及基本不等式，绝对值不等式的应用成为命题的热点，主要考查基本运算能力与推理论证能力及数形结合思想、分类讨论思想 . 真 题 感 悟 (2016· 全国 Ⅰ 卷 ) 已知函数 f ( x ) ＝ | x ＋ 1| － |2 x － 3|. (1) 在图中画出 y ＝ f ( x ) 的图象； (2) 求不等式 | f ( x )|>1 的解集 . 考 点 整 合 1. 含有绝对值的不等式的解法 2. 绝对值三角不等式 | a | － | b | ≤ | a ± b | ≤ | a | ＋ | b |. 此性质可用来解不等式或证明不等式 . 3. 基本不等式 4. 柯西不等式 (1) 设 a ， b ， c ， d 为实数，则 ( a 2 ＋ b 2 )( c 2 ＋ d 2 ) ≥ ( ac ＋ bd ) 2 ，当且仅当 ad ＝ bc 时等号成立 . 热点一　绝对值不等式的解法 [ 微题型 1] 　绝对值不等式的解法 【例 1 － 1 】 (2015· 全国 Ⅰ 卷 ) 已知函数 f ( x ) ＝ | x ＋ 1| － 2| x － a | ， a >0. (1) 当 a ＝ 1 时，求不等式 f ( x )>1 的解集； (2) 若 f ( x ) 的图象与 x 轴围成的三角形面积大于 6 ，求 a 的取值范围 . 探究提高 　 (1) 用零点分段法解绝对值不等式的步骤： ① 求零点； ② 划区间、去绝对值号； ③ 分别解去掉绝对值的不等式； ④ 取每个结果的并集，注意在分段时不要遗漏区间的端点值 .(2) 用图象法、数形结合可以求解含有绝对值的不等式，使得代数问题几何化，既通俗易懂，又简洁直观，是一种较好的方法 . 【训练 1 － 1 】 (2016· 全国 Ⅲ 卷 ) 已知函数 f ( x ) ＝ |2 x － a | ＋ a . (1) 当 a ＝ 2 时，求不等式 f ( x ) ≤ 6 的解集； (2) 设函数 g ( x ) ＝ |2 x － 1|. 当 x ∈ R 时， f ( x ) ＋ g ( x ) ≥ 3 ，求 a 的取值范围 . 解　 (1) 当 a ＝ 2 时， f ( x ) ＝ |2 x － 2| ＋ 2. 解不等式 |2 x － 2| ＋ 2 ≤ 6 得－ 1 ≤ x ≤ 3. 因此 f ( x ) ≤ 6 的解集为 { x | － 1 ≤ x ≤ 3}. (2) 当 x ∈ R 时， f ( x ) ＋ g ( x ) ＝ |2 x － a | ＋ a ＋ |1 － 2 x | ≥ |2 x － a ＋ 1 － 2 x | ＋ a ＝ |1 － a | ＋ a ， 所以当 x ∈ R 时， f ( x ) ＋ g ( x ) ≥ 3 等价于 |1 － a | ＋ a ≥ 3. ① 当 a ≤ 1 时， ① 等价于 1 － a ＋ a ≥ 3 ，无解 . 当 a ＞ 1 时， ① 等价于 a － 1 ＋ a ≥ 3 ，解得 a ≥ 2. 所以 a 的取值范围是 [2 ，＋ ∞ ). [ 微题型 2] 　含有绝对值不等式的恒成立问题 【例 1 － 2 】 (2016· 衡水大联考 ) 设函数 f ( x ) ＝ | x － 1| ， g ( x ) ＝ 2| x － a | ， a ∈ R . 探究提高 　 解答含有绝对值不等式的恒成立问题时，通常将其转化为分段函数，再求分段函数的最值，从而求出所求参数的值 . 【训练 1 － 2 】 已知函数 f ( x ) ＝ | x － a |. (1) 若不等式 f ( x ) ≤ 3 的解集为 { x | － 1 ≤ x ≤ 5} ，求实数 a 的值； (2) 在 (1) 的条件下，若 f ( x ) ＋ f ( x ＋ 5) ≥ m 对一切实数 x 恒成立，求实数 m 的取值范围 . 热点二　不等式的证明 【例 2 】 (2015· 全国 Ⅱ 卷 ) 设 a 、 b 、 c 、 d 均为正数，且 a ＋ b ＝ c ＋ d ，证明： 探究提高 　 证明不等式常用的方法有比较法、综合法、分析法、反证法、放缩法、数学归纳法等 . 【训练 2 】 (1) 已知 a ， b 都是正数，且 a ≠ b ，求证： a 3 ＋ b 3 ＞ a 2 b ＋ ab 2 ； 1. 证明绝对值不等式主要有三种方法： (1) 利用绝对值的定义脱去绝对值符号，转化为普通不等式再证明； (2) 利用三角不等式 || a | － | b || ≤ | a ± b | ≤ | a | ＋ | b | 进行证明； (3) 转化为函数问题，数形结合进行证明 . 2.(1) 研究含有绝对值的函数问题时，根据绝对值的定义，分类讨论去掉绝对值符号，转化为分段函数，然后利用数形结合解决，是常用的思想方法 . 3. 分析法是证明不等式的重要方法，当所证不等式不能使用比较法且与重要不等式、基本不等式没有直接联系，较难发现条件和结论之间的关系时，可用分析法来寻找证明途径，使用分析法证明的关键是推理的每一步必须可逆 .