思想03 数形结合思想（理）04（测试卷）-2017年高考数学二轮复习精品资料（新课标版） 12页

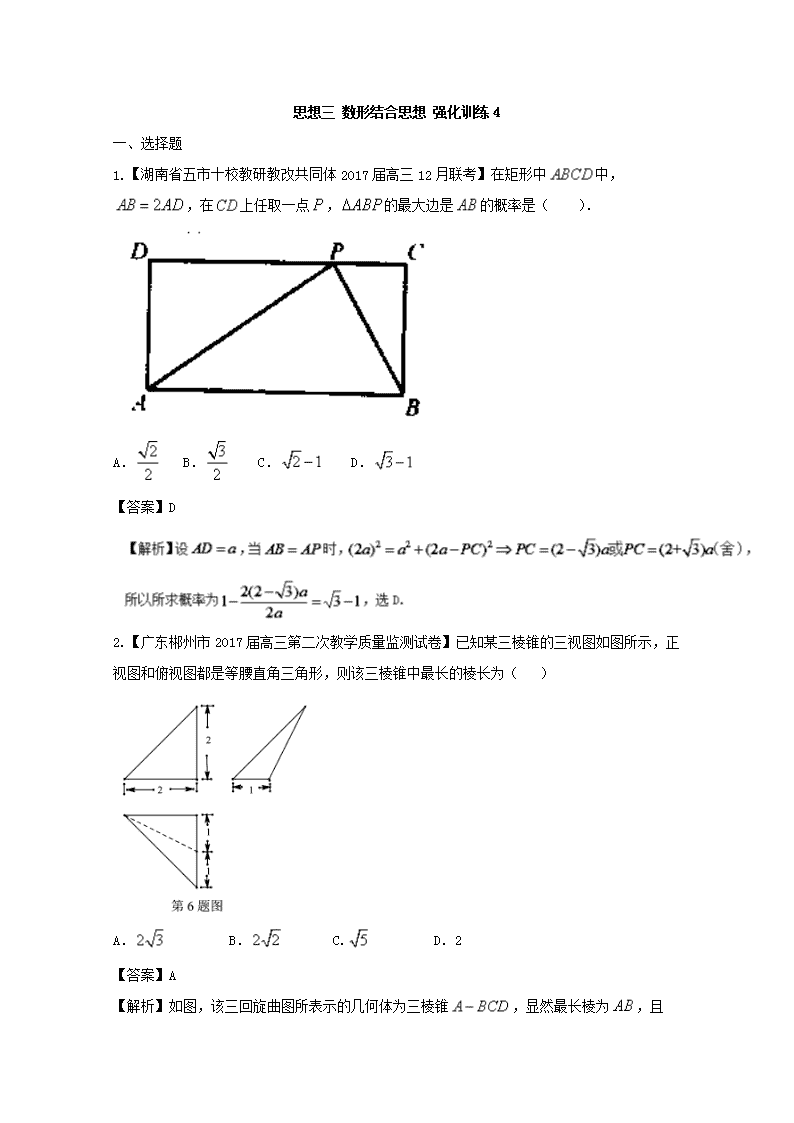
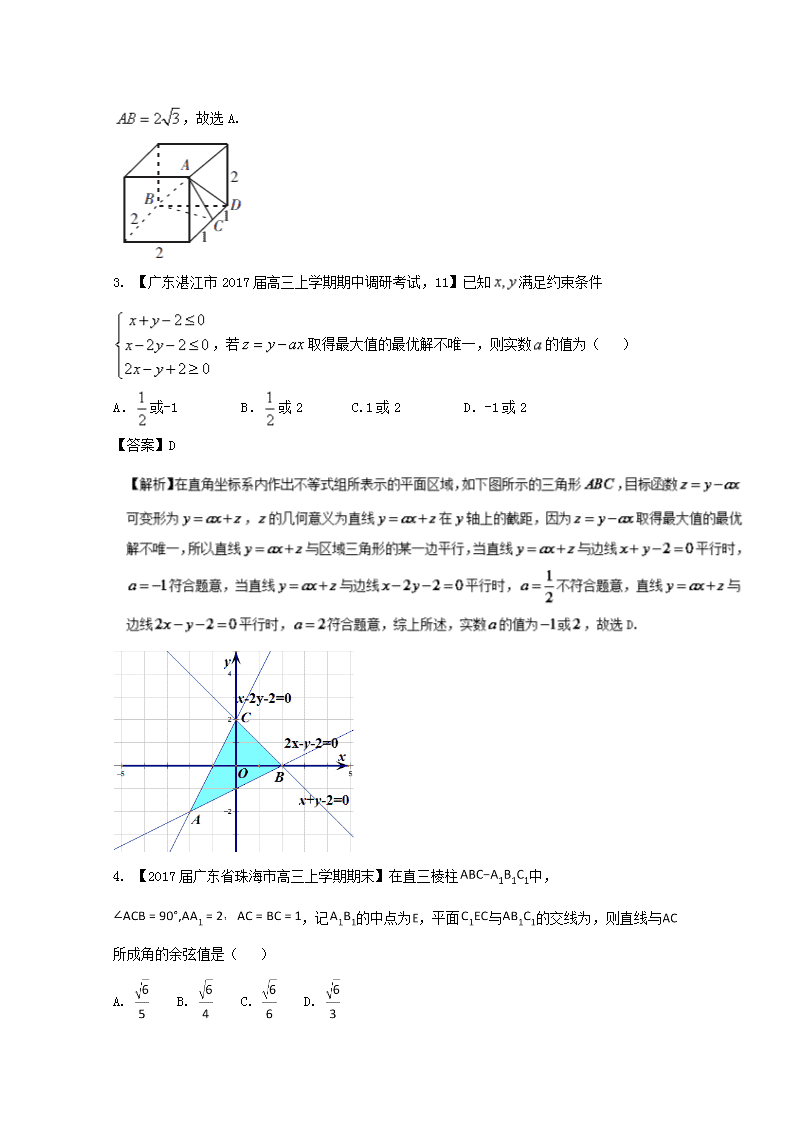
思想三 数形结合思想 强化训练4‎ 一、选择题 ‎1.【湖南省五市十校教研教改共同体2017届高三12月联考】在矩形中中，，在上任取一点，的最大边是的概率是（ ）．‎ A． B． C． D．‎ ‎【答案】D ‎2.【广东郴州市2017届高三第二次教学质量监测试卷】已知某三棱锥的三视图如图所示，正视图和俯视图都是等腰直角三角形，则该三棱锥中最长的棱长为（ ）‎ A． B． C. D．2‎ ‎【答案】A ‎【解析】如图，该三回旋曲图所表示的几何体为三棱锥，显然最长棱为，且 ‎，故选A.‎ ‎3. 【广东湛江市2017届高三上学期期中调研考试，11】已知满足约束条件，若取得最大值的最优解不唯一，则实数的值为（ ）‎ A．或-1 B．或2 C.1或2 D．-1或2‎ ‎【答案】D ‎4. 【2017届广东省珠海市高三上学期期末】在直三棱柱中，，记的中点为，平面与的交线为，则直线与所成角的余弦值是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎5. 【山西大学附属中学2017级上学期11月模块诊断，12】已知函数，若，且，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 试题分析：如图，作出函数的图象，不妨设，由可知函数的图象与直线有两个交点，而时，函数单调递增，其图象与轴交于点，‎ 所以.又，所以，，由，得，解得.‎ 由，即，解得；由，即，解得 ‎；‎ 记（），.所以当时，，函数单调递减；当时，，函数单调递增.所以函数的最小值为；而，.所以 ‎6. 【广东2017届高三上学期阶段测评（一）】执行如图所示的程序框图，若，则的最小值为（ ）‎ A．2 B．3 C.4 D．5‎ ‎【答案】A ‎【解析】程序框图的功能为求分段函数的函数值，如图可知，当或时符合题意，∴.选A.‎ ‎7. 【山西省太原市2017届高三上学期阶段性测评（期中）】设是定义在上的奇函数，当时，, 则不等式的解集为 （ ）‎ A． B． C. D．‎ ‎【答案】A ‎【解析】由题意作出函数的图象（如下图所示），由图可知不等式的解集为，故选A.‎ ‎8. 【2017届甘肃省高台县第一中学高三上学期期末】已知函数满足：①定义域为；②，都有；③当时，，则方程在区间内解的个数是（ ）‎ A. 5 B. 6 C. 7 D. 8‎ ‎【答案】A ‎【解析】依题意画出图像如下图所示，由图可知，解的个数为.‎ ‎9.【2017届内蒙古包头市十校高三联考】在正方体中，点在线段上运动，则异面直线与所成角的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】如下图： ,所有异面直线所成的角为 ,当点在线段上运动时，求的取值范围，点不能与重合，与点重合时，最大，最大为 ，的取值范围是 所以异面直线所成角的取值范围是，故选D.‎ ‎10. 【2017届湖南省衡阳市高三上学期期末】在中，边上的高为在上，点位于线段上，若，则向量在向量上的投影为（ ）‎ A. 或 B. 1 C. 1或 D. ‎ ‎【答案】A ‎【解析】中，，∴，∵，|，∴ ，∵边上的高线为，点位于线段 上，建立平面直角坐标系，如图所示；则、、设 ，则，∴，∴，∴，即，求得，∴；则， ；∵，∴，解得或；∴向量在向量上的投影为，当时，；当时，．即向量在向量上的投影为或，故选A.‎ 二、填空题 ‎11. 【安徽省“皖南八校”2017届高三第二次联考】如图，四棱锥中，，四边形为正方形，，四棱锥的五个顶点都在一个球面上，则这个球的表面积是 ．‎ ‎【答案】‎ ‎【解析】由题意得球的直径为，球的表面积是 ‎12. 【广东省汕头市2017届高三上学期期末】为了应对日益严重的气候问题，某气象仪器科研单位研究出一种新的“弹射型”气候仪器，这种仪器可以弹射到空中进行气候观测，如图所示，三地位于同一水平面上，这种仪器在地进行弹射实验，观测点两地相距100米，，在地听到弹射声音比地晚秒（已知声音传播速度为340米/秒），在地测得该仪器至高点处的仰角为，则这种仪器的垂直弹射高度 ．‎ ‎【答案】米 ‎14. 【2017届湖南师大附中高三上学期月考三】如图，一块均匀的正三角形面的钢板的质量为，在它的顶点处分别受力，每个力同它相邻的三角形的两边之间的角都是60°，且.要提起这块钢板，均要大于，则的最小值为 ．‎ ‎【答案】‎ ‎【解析】由已知可得三个力的合力的大小为 ‎.‎ A B C V O 三、解答题 ‎15. 【山东省枣庄市2017届高三上学期期末】如图，在平面四边形中，.‎ ‎（1）若与的夹角为，求的面积；‎ ‎（2）若为的中点，为的重心（三条中线的交点），且与互为相反向量求的值.‎ ‎【解析】(1)，‎ ‎.‎ ‎(2) 以为原点，所在直线为轴，建立如图所示的平面直角坐标系.则，设，则，因为与互为相反向量，所以.因为为的重心，所以，即,因此.由题意，,即..‎ ‎16. 【广东省汕头市2017届高三上学期期末】如图，四棱锥中，底面为菱形，底面，，，是上的一点，.‎ ‎（1）证明：平面；‎ ‎（2）设二面角为，求直线与平面所成角的大小.‎ 解法二：以为坐标原点，射线为轴的正半轴，建立如图所示的空间直角坐标系，设，其中，则，于是，从而，故，又，所以平面.‎ ‎（2），设为平面的法向量，则 ‎，即且，令，则，设为平面的法向量，则，即且，令，则，所以，因为面面，故，即，故，于是，，，所以．因为与平面所成角和互余，故与平面所成角的角为.‎ ‎17. 【福建省福州外国语学校2017届高三适应性考试（三）】已知，函数．‎ ‎（1）若，求的单调递增区间；‎ ‎（2）函数在上的值域为，求，需要满足的条件．‎ ‎【解析】（1）因为，，如图．所以的单调递增区间为，．‎ ‎（2）因为在上的值域为，所以，即，‎ ‎（i）当时，，所以时，‎ ‎，又，所以，得，此时，而，所以得，所以 ‎（ii）当时，，所以，①当时，，所以，得，；②当时，,所以，所以，所以或，不成立．由（i）、（ii）可知或 ‎ ‎