2020届二轮复习不等式的基本性质课件（12张）（全国通用） 12页

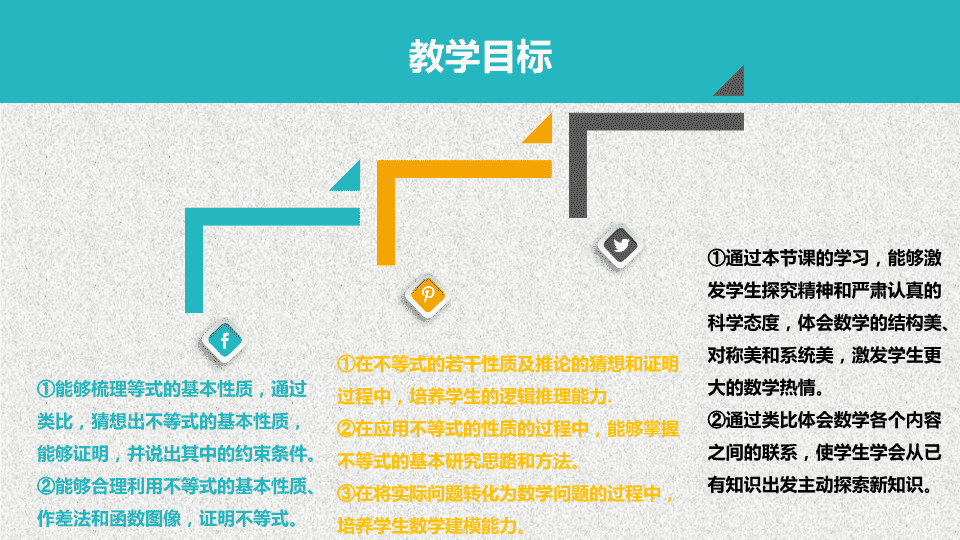
展示流程 1 2 3 4 教 材 分析 教法 分析 学法分析 教学过程 展示 教材 的地位和 作用 本节课是人教版《数学》必修 5 第三章第一节不等关系与不等式第二课时的内容．它是在掌握等式的基本性质的基础上，类比等式的基本性质，通过考察“运算中的不变性”而获得不等式的基本性质的过程，是系统地建立求解或证明不等式的理论依据，因此本课时是本章乃至高中数学的重要基础性内容之一 . 教学目标 ①能够梳理等式的基本性质，通过类比，猜想出不等式的基本性质，能够证明，并说出其中的约束条件。 ②能够合理利用不等式的基本性质、作差法和函数图像，证明不等式。 ①在不等式的若干性质及推论的猜想和证明过程中，培养学生的逻辑推理能力. ②在应用不等式的性质的过程中，能够掌握不等式的基本研究思路和方法。 ③在将实际问题转化为数学问题的过程中，培养学生数学建模能力。 ①通过本节课的学习，能够激发学生探究精神和严肃认真的科学态度，体会数学的结构美、对称美和系统美，激发学生更大的数学热情。 ②通过类比体会数学各个内容之间的联系，使学生学会从已有知识出发主动探索新知识。 教学的重点与难点 Key point difficulty Success 教学重点 教学难点 理解不等式的基本性质及推论，能利用基本性质证明不等式。 ①探索不等式的基本性质的过程与方法。 ②将实际问题转化为数学问题的过程中的数学建模。 ③证明不等式的倒数性质和性质 7 、 8 中的数形结合。 教法： 探究—建构 创设情景 类比归纳 探索创新 “探究—建构” 是指运用指导学生积极探究的方式，建立知识结构和能力结构，形成自身认知结构，实现心理结构的自我建构的教学。该教学法以发展学生探究性思维为目的，以学科基本结构为主要内容，以建立良好的认识结构为手段，以问题为中心。 本 节课通过生活中的打水问题出发，让学生发现问题，通过数学建模抽象为数学问题 ， 复习 作差法，引入不等式的基本性质，利用类比、归纳等数学思想总结出不等式的八条基本性质，并将幂函数的性质与图像贯穿始终，通过小组探讨以及自主思考有所探究与发现，激发学习兴趣。 学法：自主探究、合作交流 自主 探究 合作交流 建构主义 理论认为“学习是学生主动建构知识的过程”，强调学生的主动性。若数学概念的提出脱离了学生的主动参与，那数学课堂没有一丝活跃的气氛，所以教师在讲授知识的过程中， 要注重培养学生的自主学习能力和合作探究能力 ，这样学生才能以更大的热情投入到学习中去。本节课设计了大量的自主探索和小组讨论环节，充分发挥学生在学习中的主体性。 教学过程 框架 实际情境 引入课题 类比等式，猜想得到性质 1-4 类比猜想， 得到倒数性质 类比探究、猜想并证明 5-8 总结提升 课后拓展 数学建模、引入课题 提出问题 数学抽象 作差证明 引入课题 “打水”的实际问题如何转化为数学问题 ? 如何提炼出表达式？ 如何用作差法证明？ 本节课将深入研究不等式及其性质。 设计意图 1 、从实际问题出发，激发学生的学习兴趣，在学生发现和解决问题中，感受数学的 应用性 。 2 、学生经历数学建模的全过程，提升学生解决问题的能力，提高实践能力，增强应用 意识 。 视频 1 类比等式，猜想验证 提出问题 类比猜想 作差证明 展示评价 回顾 等式 的 性质 . 类比 等式性质猜想 出 不等式 的性质 . 教师示范证明，引导学生用作差法证明其他性质 . 教师请学生上台展示并点评 . 设计意图 1 、体现了核心素养中“逻辑推理”中的类比，不等式与等式有很多的类似之处，从等式的性质出发，通过类比进而提出不等式的问题和作出新发现。 2 、为后面的性质 5— 性质 8 的得出和性质 5 、 6 的证明做 铺垫 。 视频 2 继续类比、猜想倒数性质 提出问题 类比等式 进行猜想 小组展示进行证明 得出结论 总结提升 等式的倒数性质是什么？ 类比等式 的 倒数 性质 ，不等式是否具有这样的 性质 ，小组猜想 . 利用作差、不等式的性质、反比例图像三种方法进行证明 . 不等式有三条倒数性质，利用数形结合的思想。 设计意图 1 、 在 对不等式的倒数性质进行证明过程中体现了核心素养 “直观想象”中的数形 结合 。 2 、 为后续 性质的证明作铺垫 。 视频 3 引入性质 5 、 6 、 7 、 8 提出问题 学生探索进行证明 继续思考与提问 数形 结合进行证明 前面 在 不等式两边加、乘了相同的数，那在不等式两边加、乘不同的数，是否也具有保持不等号不变或改变的特性？ 小组展示，得到猜想并得出证明，教师点评。 除了加减乘除四则运算，还有什么运算 ? 在不等式中是否成立？小组继续猜想并证明。 学生发现这时用作差法难以证明，引导学生构造出幂函数进行证明 . 设计意图 1、鼓励学生 大胆 猜想 。 2、通过举反例对学生错误的猜想做分析，对正确的猜想进行证明，让学生有成功的体验，突破本节课重难点。 3、继续深化“类比”思想，通过对加或乘相同与不同的数之间的类比，不断的提升教学效果。 视频 4 拓展升华、总结提升 提出问题 性质证明 数学抽象 拓展升华 课堂小结 总结提升 课后思考 与作业 回到活动一，课前用作差进行了 证明， 能否用性质进行证明 ？ 运用性质 4 证明 . 把活动一所得的数学表达式进行抽象 ， 引导学生提炼出排序不等式的二维形式 本节课你学到了什么 ？ 掌握 了什么数学思想和方法？ 思考：将活动一的 2 个人改为 10 个人如何解决？ 设计意图 1 、 让 学生感受到新学到的知识可以解决之前不曾解决的问题，激发学习的兴趣。 2 、培养学生抽象与概括的思想方法。进而升华思想，体会不等式性质的实质，拓展思维与眼界，体会数学的美 。 3 、 培养 学生课后反思的习惯。检测学生当堂学习效果，为教师提供准确的反馈，为学生提供更准确的个性化 辅导 。 视频 5