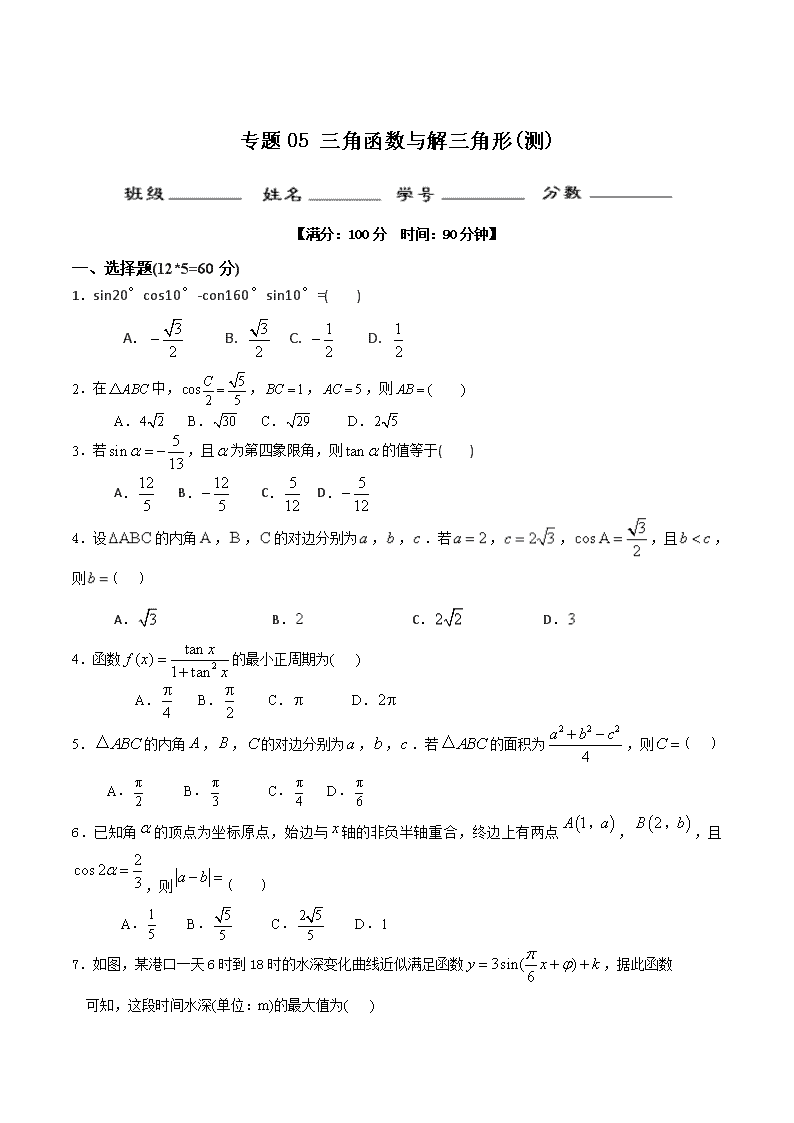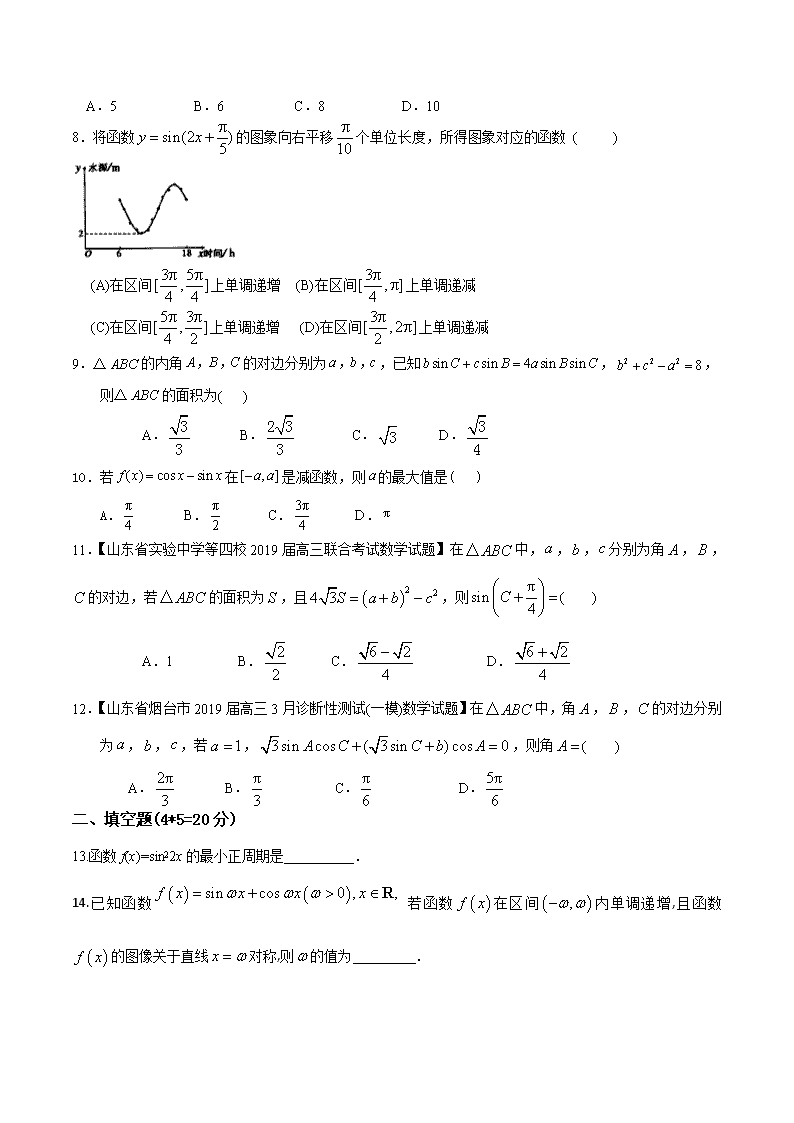2020年高考数学(理)二轮复习讲练测 专题05 三角函数与解三角形（测）（原卷版） 4页

专题05 三角函数与解三角形(测)‎ ‎【满分：100分 时间：90分钟】‎ 一、选择题(12*5=60分)‎ ‎1．sin20°cos10°-con160°sin10°=( )‎ ‎ A． B. C. D. ‎ ‎2．在中，，，，则( )‎ A． B． C． D．‎ ‎3．若，且为第四象限角，则的值等于( )‎ A． B． C． D． ‎ ‎4．设的内角，，的对边分别为，，．若，，，且，则( )‎ A． B． C． D．‎ ‎4．函数的最小正周期为( )‎ A． B． C． D．‎ ‎5．的内角，，的对边分别为，，．若的面积为，则( )‎ A． B． C． D．‎ ‎6．已知角的顶点为坐标原点，始边与轴的非负半轴重合，终边上有两点，，且，则( )‎ A． B． C． D．‎ ‎7．如图，某港口一天6时到18时的水深变化曲线近似满足函数，据此函数 可知，这段时间水深(单位：m)的最大值为( )‎ A．5 B．6 C．8 D．10‎ ‎8．将函数的图象向右平移个单位长度，所得图象对应的函数 ( )‎ ‎(A)在区间上单调递增 (B)在区间上单调递减 ‎(C)在区间上单调递增 (D)在区间上单调递减 ‎9．△的内角的对边分别为，已知，，则△的面积为( )‎ A． B． C． D．‎ ‎10．若在是减函数，则的最大值是( )‎ A． B． C． D．‎ ‎11．【山东省实验中学等四校2019届高三联合考试数学试题】在中，，，分别为角，，的对边，若的面积为，且，则( )‎ A．1 B． C． D．‎ ‎12．【山东省烟台市2019届高三3月诊断性测试(一模)数学试题】在中，角，，的对边分别为，，，若，，则角( )‎ A． B． C． D．‎ 二、填空题(4*5=20分)‎ ‎13.函数f(x)=sin22x的最小正周期是__________．‎ ‎14.已知函数 若函数在区间内单调递增,且函数的图像关于直线对称,则的值为 ．‎ ‎15. 已知，则的值是 .‎ ‎16．在中，角所对的边分别为，，的平分线交于点D，且，则的最小值为 ．‎ 二、解答题(6*12=70分)‎ ‎17．【北京市昌平区2019届高三5月综合练习(二模)数学试题】已知函数.‎ ‎(1)求的值；(2)当时，不等式恒成立，求实数的取值范围．‎ ‎18、△ABC的内角A，B，C的对边分别为a，b，c，已知．‎ ‎(1)求B；‎ ‎(2)若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围．‎ ‎19、设函数.‎ ‎(1)已知函数是偶函数，求的值；‎ ‎(2)求函数的值域．‎ ‎20、在平面四边形中，，，，.‎ ‎(1)求； (2)若，求.‎ ‎21、已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P()．‎ ‎(1)求sin(α+π)的值；‎ ‎(2)若角β满足sin(α+β)=，求cosβ的值．‎ ‎22．已知函数．‎ ‎(1)求函数的最小正周期；‎ ‎(2)将函数的图象向右平移个单位长度，再向下平移()个单位长度后得到函数的图象，且函数的最大值为2．‎ ‎(ⅰ)求函数的解析式；‎ ‎(ⅱ)证明：存在无穷多个互不相同的正整数，使得．‎