河南省新乡市2019届高三第三次模拟测试数学（理）试卷 6页

新乡市2019届高三第三次模拟测试 数学试卷（理科）‎ 考生注意：‎ ‎ 1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试时间120分钟．‎ ‎ 2．请将各题答案填写在答题卡上．‎ ‎ 3．本试卷主要考试内容：高考全部内容．‎ 第Ⅰ卷 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（1＋i）（2＋i）（3＋i）＝‎ A．－10i B．10i C．－10 D．10‎ ‎2．已知集合A＝{x｜x2－4x＜5}，则 ‎ A．－1．2∈A B．30．9A ‎ C．log230∈A D．A∩N＝{1，2，3，4}‎ ‎3．设向量el，e2是平面内的一组基底，若向量a＝－3el－e2与b＝el－λe2共线，则λ＝‎ ‎ A． B．－ C．－3 D．3‎ ‎4．若f（x）＝a－2＋asin2x为奇函数，则曲线y＝f（x）在x＝0处的切线的斜率为 ‎ A．－2 B．－4 C．2 D．4‎ ‎5．已知函数f（x）在（－∞，＋∞）上单调递减，且当x∈[－2，1]时，f（x）＝x2－2x－4，则关于x的不等式f（x）＜－1的解集为 A．（－1，＋∞） B．（－∞，3） ‎ C．（－1，3） D．（－∞，－1）‎ ‎6．某图形由一个等腰直角三角形，一个矩形（矩形中的阴影部分为半圆），一个半圆组成，从该图内随机取一点，则该点取自阴影部分的概率为 A． B．‎ ‎ C． D．‎ ‎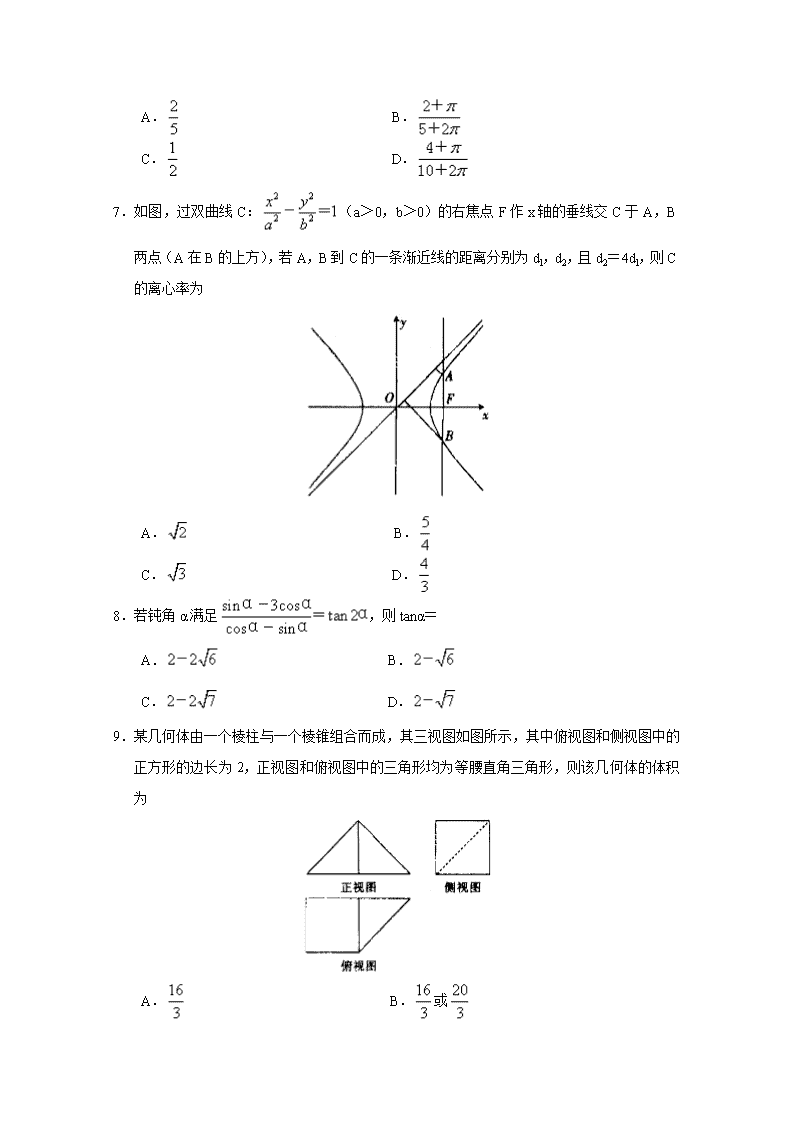7．如图，过双曲线C：（a＞0，b＞0）的右焦点F作x轴的垂线交C于A，B两点（A在B的上方），若A，B到C的一条渐近线的距离分别为dl，d2，且d2＝4dl，则C的离心率为 A． B．‎ ‎ C． D．‎ ‎8．若钝角α满足，则tanα＝‎ ‎ A． B． ‎ C． D．‎ ‎9．某几何体由一个棱柱与一个棱锥组合而成，其三视图如图所示，其中俯视图和侧视图中的正方形的边长为2，正视图和俯视图中的三角形均为等腰直角三角形，则该几何体的体积为 A． B．或 ‎ C． D．或6‎ ‎10．设a＝lg 6，b＝lg 20，则log23＝‎ A． B． C． D．‎ ‎11．在△ABC中，角A，B，C所对的边分别是a，b，c．已知a∈（，），b＝1，且abcos C＋ccos A＝abc，则cos B的取值范围为 ‎ A．（，） B．（，） C．（0，） D．（0，）‎ ‎12．在直角坐标系xOy中，直线y＝kx＋1与抛物线C：x2＝4y交于A，B两点，若∠AOB＝120°，则k＝‎ ‎ A． B． C． D．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上．‎ ‎13．某校有高一学生n名，其中男生数与女生数之比为6 ：5，为了解学生的视力情况，现要求按分层抽样的方法抽取一个样本容量为的样本，若样本中男生比女生多12人，则n＝__________．‎ ‎14．一个球的内接正方体的表面积为32，则该球的体积为__________．‎ ‎15．已知a＞0，则当的展开式的常数项（即不含x的项）取得最小值时，a＝___________．‎ ‎16．某农户计划种植莴笋和西红柿，种植面积不超过30亩，投入资金不超过25万元，假设种植莴笋和西红柿的产量、成本和售价如下表：‎ ‎ 那么，该农户一年种植总利润（总利润＝总销售收入－总种植成本）的最大值为__________万元．‎ 三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每道试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎（一）必考题：共60分．‎ ‎17．（12分）‎ 在数列{}中，＝1，且，2n，成等比数列．‎ ‎（1）求，，；‎ ‎（2）求数列{}的前项和．‎ ‎18．（12分）‎ ‎ 以下是新兵训练时，某炮兵连8周中炮弹对同一目标的命中情况的柱状图：‎ ‎（1）计算该炮兵连这8周中总的命中频率p0，并确定第几周的命中频率最高；‎ ‎（2）以（1）中的p0作为该炮兵连炮兵甲对同一目标的命中率，若每次发射相互独立，且炮兵甲发射5次，记命中的次数为X，求X的方差；‎ ‎（3）以（1）中的p0作为该炮兵连炮兵对同一目标的命中率，试问至少要用多少枚这样的炮弹同时对该目标发射一次，才能使目标被击中的概率超过0．99?（取lg 0．4＝‎ ‎－0．398）‎ ‎19．（12分）‎ ‎ 如图，在三棱锥P－ABC中，PA⊥平面ABC，且PA＝AB＝BC＝2，AC＝．‎ ‎（1）证明：三棱锥P－ABC为．‎ ‎（2）若D为棱PB的中点，求二面角D－AC－P的余弦值．‎ ‎ 注：在《九章算术》中鳖臑（nào）是指四面皆为直角三角形的三棱锥．‎ ‎20．（12分）‎ ‎ 已知椭圆（a＞b＞0）的短轴长为2，且椭圆的—个焦点在圆（x－2）2＋（y－3）2＝18上． ‎ ‎（1）求椭圆的方程；‎ ‎（2）已知椭圆的焦距小于4，过椭圆的左焦点F的直线l与椭圆相交于A，B两点，若｜AF｜＝3｜FB｜，求｜AB｜．‎ ‎21．（12分）‎ 已知函数（a∈R）．‎ ‎（1）讨论函数在（1，＋∞）上的单调性；‎ ‎（2）若a≥0，不等式x2f（x）＋a≥2－e对x∈（0，＋∞）恒成立，求a的取值范围．‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．‎ ‎22．[选修4－4：坐标系与参数方程]（10分）‎ ‎ 在直角坐标系xOy中，曲线C的参数方程为（α为参数）．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，已知点A的极坐标为（3，）．‎ ‎（1）求曲线C的极坐标方程；‎ ‎（2）过A作曲线C的切线，切点为M，过O作曲线C的切线，切点为N，求．‎ ‎23．[选修4－5：不等式选讲]（10分）‎ ‎ 已知函数．‎ ‎（1）若a＝1，证明：f（｜x｜）≥5．‎ ‎（2）若f（1）＜5a2，求a的取值范围．‎