江苏省启东中学2017高考数学押题卷4 13页

卷4‎ 一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应的位置上．‎ ‎1．若集合A={x|x＞2}，B={x|x≤3}，则A∩B= ▲ ．‎ 答案： 解析：A∩B= ‎ ‎2．函数y=sin2x+cos2x的最小正周期是 ▲ ．‎ 答案：π 解析：y=sin2x+cos2x=2 sin(2 x+60º) ÞT=2π/2= π ‎3．已知(a+i)2=2i，其中i是虚数单位，那么实数 a= ▲ ．‎ 答案：1‎ 解析：(a+i)2= a2+2 ai+ i2= a2-1+2 ai=2i Þ a=1‎ ‎4．已知向量a与b的夹角为60º，且|a|=1，|b|=2，那么的值为 ▲ ．‎ 答案：7‎ 解析：=a2+ b2+2ab = a2+ b2+2|a||b| cos60º=12+22+2x1x2=7‎ ‎5．底面边长为‎2m，高为‎1m的正三棱锥的全面积为 ▲ m2．‎ 答案：‎ 解析：如图所示，正三棱锥，为顶点在底面内的射影，则为正的垂心，过作于，连接。‎ 则，且，在中，。‎ 于是，，。‎ 所以。‎ ‎6．若双曲线的焦点到渐近线的距离为，则实数k的值是 ▲ ．‎ 答案：8‎ 解析：法一：双曲线的渐近线方程为；焦点坐标是。‎ 由焦点到渐近线的距离为，不妨。解得。‎ 法二：可以将问题变为“若椭圆的离心率为，则实数k= ”，这时需要增加分 类讨论的意思 法三：结论法: 在双曲线中，双曲线的焦点到渐近线的距离为b 【在本题中，则b 2=k=（)2=8】‎ ‎7．若实数x，y满足则z=x+2y的最大值是 ▲ ．‎ 答案：2‎ 解析：满足题中约束条件的可行域如图所示。‎ 目标函数取得最大值，‎ 即使得函数在轴上的截距最大。‎ 结合可行域范围知，当其过点时，。‎ ‎8．对于定义在R上的函数f(x)，给出三个命题：‎ ‎ ①若，则f(x)为偶函数；‎ ‎ ②若，则f(x)不是偶函数；‎ ‎ ③若，则f(x)一定不是奇函数．‎ ‎ 其中正确命题的序号为 ▲ ．‎ 答案：②‎ 解析：命题③学生很容易判为真命题．‎ 反例：函数是奇函数，且满足．‎ 请注意以下问题：既是奇函数又是偶函数的函数是否唯一？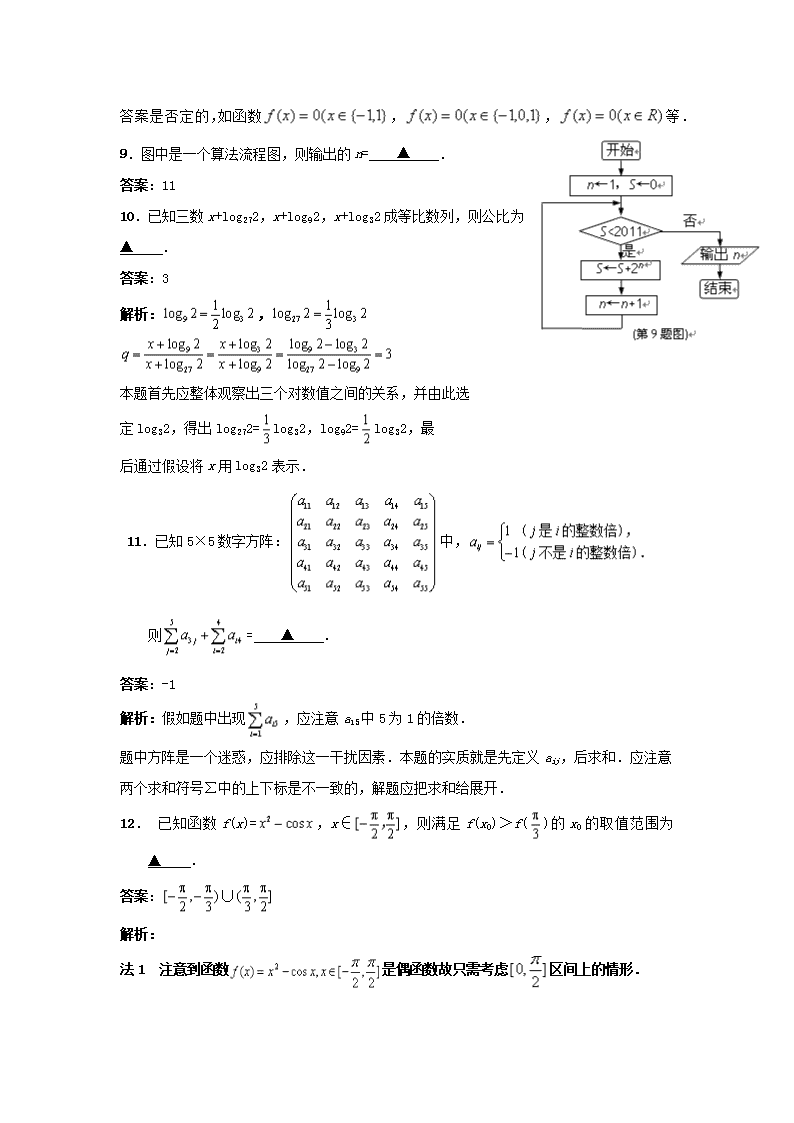‎ 答案是否定的，如函数，，等．‎ ‎9．图中是一个算法流程图，则输出的n= ▲ ．‎ 答案：11‎ ‎10．已知三数x+log272，x+log92，x+log32成等比数列，则公比为 ▲ ．‎ 答案：3‎ 解析：， ‎ 本题首先应整体观察出三个对数值之间的关系，并由此选 定log32，得出log272=log32，log92=log32，最 后通过假设将x用log32表示．‎ ‎11．已知5×5数字方阵：中，‎ 则= ▲ ．‎ 答案：-1‎ 解析：假如题中出现，应注意a15中5为1的倍数．‎ 题中方阵是一个迷惑，应排除这一干扰因素．本题的实质就是先定义aij，后求和．应注意 两个求和符号∑中的上下标是不一致的，解题应把求和给展开．‎ ‎12． 已知函数f(x)=，x∈，则满足f(x0)＞f()的x0的取值范围为 ▲ ．‎ 答案：∪‎ 解析：‎ 法1 注意到函数是偶函数故只需考虑区间上的情形．‎ 由知函数在单调递增，‎ 所以在上的解集为，‎ 结合函数是偶函数得原问题中取值范围是．‎ 法2 ，‎ 作出函数在上的图象 并注意到两函数有交点可得取值范围是．‎ ‎13．甲地与乙地相距250公里．某天小袁从上午7∶50由甲地出发开车前往乙地办事．在上午9∶00，10∶00，11∶00三个时刻，车上的导航仪都提示“如果按出发到现在的平均速度继续行驶，那么还有1小时到达乙地”．假设导航仪提示语都是正确的，那么在上午11∶00时，小袁距乙地还有 ▲ 公里． ‎ 答案：60‎ 解析：设从出发到上午11时行了公里，则，解得，此时小袁距乙地还有‎60公里．‎ ‎14．定义在上的函数f(x)满足：①f(2x)=cf(x)(c为正常数)；②当2≤x≤4时，f(x)=1-|x-3|．若函数的所有极大值点均落在同一条直线上，则c= ▲ ．‎ 答案：1或2‎ 解析：由已知可得：当时，；‎ 当时，；当时，，‎ 由题意点共线，据得或2． ‎ 二、解答题：本大题共6小题，共计90分．请把答案写在答题卡相应的位置上．解答时应写出文字说明，证明过程或演算步骤．‎ ‎15．(本题满分14分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本，得频率分布表如下：‎ 组号 分组 频数 频率 第一组 ‎8‎ ‎0.16‎ 第二组 ‎①‎ ‎0.24‎ 第三组 ‎15‎ ‎②‎ 第四组 ‎10‎ ‎0.20‎ 第五组 ‎5‎ ‎0.10‎ 合 计 ‎50‎ ‎1.00‎ ‎(1)写出表中①②位置的数据；‎ ‎(2)为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核，分别求第三、四、五各组参加考核人数；‎ ‎(3)在(2)的前提下，高校决定在这6名学生中录取2名学生，求2人中至少有1名是第四组的概率． ‎ 解：(1) ①②位置的数据分别为12、0.3； ………………………………………………4分 ‎(2) 第三、四、五组参加考核人数分别为3、2、1； …………………………………8分 ‎(3) 设上述6人为abcdef(其中第四组的两人分别为d，e)，则从6人中任取2人的所有情形为：{ab，ac，ad，ae，af，bc，bd，be，bf，cd，ce，cf，de，df，ef}‎ 共有15种．…………………………………………………………………………10分 记“2人中至少有一名是第四组”为事件A，则事件A所含的基本事件的种数有9种． …………………………………………………………………………………12分 所以，故2人中至少有一名是第四组的概率为． ……………14分 ‎16．(本题满分14分) ‎ 如图，在三棱柱ABC-A1B‎1C1中． ‎ ‎(1)若BB1=BC，B‎1C⊥A1B，证明：平面AB1C平面A1BC1；‎ ‎(2)设D是BC的中点，E是A‎1C1上的一点，且A1B∥平面 B1DE，求的值．‎ ‎ 解：(1)因为BB1=BC，所以侧面BCC1B1是菱形，所以B‎1C⊥BC1． …………………3分 又因为B‎1C⊥A1B ，且A1B∩BC1=B，所以BC1⊥平面A1BC1， …………………5分 又B1C平面AB‎1C ，所以平面AB‎1C⊥平面A1BC1 ．……………………………7分 ‎(2)设B1D交BC1于点F，连结EF，则平面A1BC1∩平面B1DE＝EF．‎ 因为A1B//平面B1DE， A1B平面A1BC1，所以A1B//EF． …………………11分 所以＝．‎ 又因为＝，所以＝． ………………………………………14分 ‎17．(本题满分14分)‎ 在△ABC中，a2+c2=2b2，其中a，b，c分别为角A，B，C所对的边长．‎ ‎(1)求证：B≤；‎ ‎(2)若，且A为钝角，求A．‎ 解：‎ ‎(1)由余弦定理，得． ……………………………………3分 因，．………………………………………………………6分 由0＜B＜π，得 ，命题得证． ……………………………………………7分 ‎(2)由正弦定理，得． …………………………………………10分 因，故=1，于是．……………………………………12分 因为A为钝角，所以．‎ 所以(，不合，舍) ．解得． …………………14分 ‎（2）其它方法：‎ 法1 同标准答案得到，用降幂公式得到，或 ‎，展开再处理，下略．‎ 法2 由余弦定理得，结合得，‎ ‎，，展开后用降幂公式再合，下略．‎ 法3 由余弦定理得，结合得，‎ ‎，，下略 ‎18．(本题满分16分)‎ 在平面直角坐标系xOy中，已知椭圆(a＞b＞0)的离心率为，其焦点在圆x2+y2=1上．‎ ‎(1)求椭圆的方程；‎ ‎(2)设A，B，M是椭圆上的三点(异于椭圆顶点)，且存在锐角θ，使 ‎．‎ ‎ (i)求证：直线OA与OB的斜率之积为定值；‎ ‎(ii)求OA2+OB2．‎ 解：‎ ‎(1)依题意，得 c=1．于是，a=，b=1． ……………………………………2分 所以所求椭圆的方程为． ………………………………………………4分 ‎(2) (i)设A(x1，y1)，B(x2，y2)，则①，②． ‎ 又设M(x，y)，因，故 …………7分 因M在椭圆上，故．‎ 整理得．‎ 将①②代入上式，并注意，得 ．‎ 所以，为定值． ………………………………………………10分 ‎(ii)，故．‎ 又，故．‎ 所以，OA2+OB2==3． …………………………………………16分 ‎19．(本题满分16分)‎ 已知数列{an}满足：a1=a2=a3=2，an+1=a‎1a2…an-1(n≥3)，记 ‎(n≥3)．‎ ‎(1)求证数列{bn}为等差数列，并求其通项公式；‎ ‎(2)设，数列{}的前n项和为Sn，求证：n1，．……………………10分 ‎=<<，‎ ‎ 故<，于是．……………………………………16分 第(2)问，为了结果的美观，将Sn放缩范围放得较宽，并且可以改为求不小于Sn的最小正整数或求不大于Sn的最大正整数．‎ 本题（2）的方法二是错误的，请不要采用。‎ 注意 ‎=<<，‎ ‎ 故<，于是．‎ 于是。（这一步推理是错误的）‎ ‎20．(本题满分16分)‎ ‎ 设函数f(x)=ax3-(a+b)x2+bx+c，其中a＞0，b，c∈R．‎ ‎ (1)若=0，求函数f(x)的单调增区间；‎ ‎(2)求证：当0≤x≤1时，||≤．(注：max{a，b}表示a，b中的最大值)‎ 解：(1)由=0，得a=b． …………………………………………………………1分 故f(x)= ax3－2ax2+ax+c．‎ 由=a(3x2－4x+1)=0，得x1=，x2=1．…………………………………………2分 列表：‎ x ‎(-∞，)‎ ‎(，1)‎ ‎1‎ ‎(1，+∞)‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ f(x)‎ 增 极大值 减 极小值 增 由表可得，函数f(x)的单调增区间是(-∞，)及(1，+∞) ．…………………………4分 ‎(2)=3ax2-2(a+b)x+b=3．‎ ‎①当时，则在上是单调函数，‎ 所以≤≤，或≤≤，且+=a>0．‎ 所以||≤．………………………………………………………8分 ‎②当，即-a＜b＜‎2a，则≤≤．‎ ‎(i) 当-a＜b≤时，则0＜a+b≤．‎ 所以 ＝＝≥＞0．‎ 所以 ||≤． ……………………………………………………12分 ‎(ii) 当＜b＜‎2a时，则＜0，即a2+b2－＜0．‎ 所以=＞＞0，即＞．‎ 所以 ||≤．‎ 综上所述：当0≤x≤1时，||≤．……………………………16分 数学Ⅱ（附加题）‎ ‎21．【选做题】本题包括A，B，C，D共4小题，请从这4题中选做2小题，每小题10分，共20分．请在答题卡上准确填涂题目标记，解答时应写出文字说明、证明过程或演算步骤．‎ A．选修4－1：几何证明选讲 如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，求证：∠PDE=∠POC．‎ 证明：因AE=AC，AB为直径，‎ ‎ 故∠OAC=∠OAE． ……………………………………………………………3分 所以∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC．‎ 又∠EAC=∠PDE，‎ 所以，∠PDE=∠POC．…………………………………………………………10分 B．选修4－2：矩阵与变换 已知圆C：在矩阵对应的变换作用下变为椭圆，求a，b的值．‎ ‎ 解：设为圆C上的任意一点，在矩阵A对应的变换下变为另一个点，‎ 则 ，即 …………………………………………………4分 又因为点在椭圆上，所以 ．‎ 由已知条件可知， ，所以 a2=9，b2=4．‎ 因为 a>0 ，b>0，所以 a=3，b=2． …………………………………………………10分 C．选修4－4：坐标系与参数方程 ‎ 在极坐标系中，求经过三点O(0，0)，A(2，)，B(，)‎ 的圆的极坐标方程．‎ ‎ 解：设是所求圆上的任意一点，………………………………………………3分 则， ‎ ‎ 故所求的圆的极坐标方程为． …………………………………10分 ‎ 注：亦正确．‎ D．选修4－5：不等式选讲 已知x，y，z均为正数．求证：．‎ 证明：因为x，y，z都是为正数，所以． …………………3分 ‎ 同理可得． ‎ 将上述三个不等式两边分别相加，并除以2，得．………10分 ‎22．【必做题】本题满分10分．解答时应写出文字说明、证明过程或演算步骤．‎ 已知函数，其中a＞0．‎ ‎(1)若在x=1处取得极值，求a的值；‎ ‎(2)若的最小值为1，求a的取值范围． ‎ 解：(1) ．‎ 因在处取得极值，故，解得a=1 (经检验)．……………………4分 ‎(2)，因 ，故ax+1＞0，1+x＞0．‎ 当a≥2时，在区间上，递增，的最小值为f(0)=1．‎ 当0