数学理卷·2017届河南省扶沟二中高三第三次模拟考试（2017 12页

扶沟二高2017年高三年级第三次模拟考试 数 学（理科）‎ ‎ 本试卷分试题卷和答题卡两部分。试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），共4页；答题卡共6页。满分为150分，考试时间为120分钟。考生作答时，请按要求把答案涂、写在答题卡规定的范围内，超出答题框或答在试题卷上的答案无效。考试结束只收答题卡。‎ 第Ⅰ卷 （选择题，共60分）‎ 一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．已知集合A＝{ x｜＜1}，B＝{ x｜－4x－12＞0}，则（CRA）∩B＝‎ A．[－3，－2） B．（－∞，－3] ‎ C．[－3，－2）∪（6，＋∞） D．（－3，－2）∪（6，＋∞）‎ ‎2．已知复数z满足i·z＝，则复数z在复平面内对应的点在 ‎ A．第四象限 B．第三象限 C．第二象限 D．第一象限 ‎3．已知随机变量X＋Y＝10，若X～B（10，0．6），则E（Y），D（Y）分别是 ‎ A． 6和2．4 B．4和5．‎6 C．4和2．4 D．6和5．6‎ ‎4．已知椭圆C：（a＞b＞0）的离心率为，双曲线的渐近线与椭 圆C有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为 A． B．‎ C． D．‎ ‎5．在如图的程序框图中，任意输入一次 x（0≤x≤1）与y（0≤y≤1），则能输出 ‎“恭喜中奖!”的概率为 A． B． ‎ C． D． ‎ ‎6．若sin（－α）＝，则cos（＋2α）＝‎ A． B．－ ‎ C． D．－‎ ‎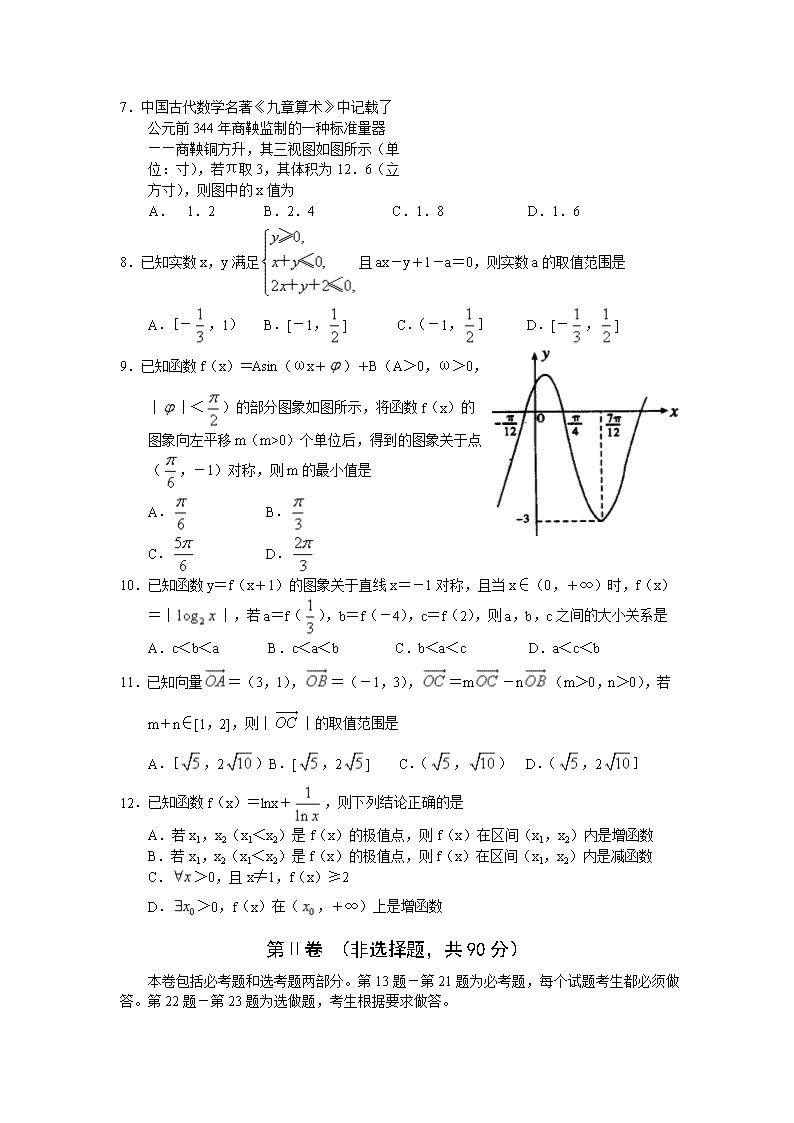7．中国古代数学名著《九章算术》中记载了 公元前344年商鞅监制的一种标准量器 ‎——商鞅铜方升，其三视图如图所示（单 位：寸），若π取3，其体积为12．6（立 方寸），则图中的x值为 A． 1．2 B．2．‎4 C．1．8 D．1．6‎ ‎8．已知实数x，y满足且ax－y＋1－a＝0，则实数a的取值范围是 ‎ A．[－，1） B．[－1，] C．（－1，] D．[－，]‎ ‎9．已知函数f（x）＝Asin（ωx＋）＋B（A＞0，ω＞0，‎ ‎｜｜＜）的部分图象如图所示，将函数f（x）的 图象向左平移m（m>0）个单位后，得到的图象关于点 ‎（，－1）对称，则m的最小值是 ‎ A． B．‎ ‎ C． D．‎ ‎10．已知函数y＝f（x＋1）的图象关于直线x＝－1对称，且当x∈（0，＋∞）时，f（x）＝｜｜，若a＝f（），b＝f（－4），c＝f（2），则a，b，c之间的大小关系是 ‎ A．c＜b＜a B．c＜a＜b C．b＜a＜c D．a＜c＜b ‎11．已知向量＝（3，1），＝（－1，3），＝m－n（m＞0，n＞0），若m＋n∈[1，2]，则｜｜的取值范围是 ‎ A．[，2）B．[，2] C．（，） D．（，2]‎ ‎12．已知函数f（x）＝lnx＋，则下列结论正确的是 ‎ A．若x1，x2（x1＜x2）是f（x）的极值点，则f（x）在区间（x1，x2）内是增函数 ‎ B．若x1，x2（x1＜x2）是f（x）的极值点，则f（x）在区间（x1，x2）内是减函数 ‎ C．＞0，且x≠1，f（x）≥2‎ ‎ D．＞0，f（x）在（，＋∞）上是增函数 第Ⅱ卷 （非选择题，共90分）‎ ‎ 本卷包括必考题和选考题两部分。第13题－第21题为必考题，每个试题考生都必须做答。第22题－第23题为选做题，考生根据要求做答。‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．已知点F（3，0）是双曲线（m＞0）的一个焦点，则此双曲线的离心率为_____________．‎ ‎14．已知球O的球面上四点A，B，C，D，满足DA⊥平面ABC，AB⊥BC，DA＝AB＝BC＝，则球O的体积等于____________．‎ ‎15．在△ABC中，内角A，B，C所对的边分别为a，b，c，且b＝，sinC＝（sinA＋cosA）sinB，则AC边上的高的最大值为____________．‎ ‎16．下列结论正确的是_____________．‎ ‎ ①的展开式中的系数为－210；‎ ‎②在吸烟与患肺病这两个分类变量的计算中，从独立性检验知，有99％的把握认为吸烟 与患肺病有关系时，我们说某人吸烟，那么他有99％的可能患肺病；‎ ‎③已知命题“若函数f（x）＝－mx在（0，＋∞）上是增函数，则m≤1”的逆否命 题是“若m＞1，则函数f（x）＝－mx在（0，＋∞）上是减函数”，是真命题；‎ ‎ ④不等式－（‎2a－3）x－1＞0对＞1恒成立的充要条件是0≤a≤2．‎ 三、解答题（本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分12分）‎ 在数列{} 中，设f（n）＝，且f（n）满足f（n＋1）－2f（n）＝（n∈N﹡），‎ 且a1＝1． ‎ ‎ （Ⅰ）设＝，证明数列{}为等差数列； ‎ ‎ （Ⅱ）求数列{－1}的前n项和．‎ ‎18．（本小题满分12分）‎ 某羽绒服卖场为了解气温对营业额的影响。营业员 小孙随机记录了该店3月份上旬中某5天的日营业 额 y（单位：千元）与该地当日最低气温x（单位：‎ ‎℃）的数据，如表：‎ ‎ （Ⅰ）求y关于x的回归直线方程＝x＋；‎ ‎ （Ⅱ）若天气预报明天的最低气温为‎120℃‎，用所求回归方程预测该店明天的营业额；‎ ‎ （Ⅲ）设该地3月份的日最低气温X～N（μ, ），其中μ近似为样本平均数，‎ 近似为样本方差，求P（0．6＜x＜10．2）．‎ ‎19．（本小题满分12分）‎ ‎ 在三棱柱ABC－A1B‎1C1中，AC＝BC＝2，∠ACB＝120°，D为A1B1的中点．‎ ‎ （Ⅰ）证明：A‎1C∥平面BC1D；‎ ‎ （Ⅱ）若A‎1A＝A‎1C，点A1在平面ABC的射影在AC ‎ 上，且BC与平面BC1D所成角的正弦值为 ‎，求三棱柱ABC－A1B‎1C1的体积．‎ ‎20．（本小题满分12分）‎ 已知O为坐标原点，抛物线C：＝nx（n＞0）在第一象限内的点P(1，t)到焦点的距 离为2，曲线C在点P处的切线交x轴于点Q，直线l1经过点Q且垂直于x轴．‎ ‎ （Ⅰ）求线段OQ的长；‎ ‎ （Ⅱ）设不经过点P和Q的动直线l2：x＝my＋b交曲线C于点A和B，交l1于点E，若直线PA，PE，PB的斜率依次成等差数列，试问：l2是否过定点?请说明理由．‎ ‎21．（本小题满分12分）‎ ‎ 已知函数f（x）＝lnx－2ax（其中a∈R）．‎ ‎ （Ⅰ）当a＝2时，求函数f（x）的图象在x＝1处的切线方程；‎ ‎ （Ⅱ）若f（x）≤2恒成立，求a的取值范围；‎ ‎ （Ⅲ）设g（x）＝f（x）＋，且函数g（x）有极大值点x0，求证：＋1＋ ＞0．‎ ‎ ‎ 请考生在第22、23两题中任选一题作答，如果两题都做，则按照所做的第一题给分；‎ 作答时，请用2B铅笔将答题卡上相应的题号涂黑。‎ ‎22．（本小题满分10分）选修4—4：坐标系与参数方程 ‎ 已知直线l：ρsin（θ＋）＝m，曲线C：‎ ‎ （Ⅰ）当m＝3时，判断直线l与曲线C的位置关系； ‎ ‎ （Ⅱ）若曲线C上存在到直线l的距离等于的点，求实数m的范围．‎ ‎23．（本小题满分10分）选修4—5：不等式选讲 ‎ 设函数f（x）＝｜x＋2｜＋｜x－1｜．‎ ‎ （Ⅰ）求f（x）的最小值及取得最小值时x的取值范围；‎ ‎（Ⅱ）若集合{x｜f（x）＋ax－1＞0}＝R，求实数a的取值范围．‎ 扶沟二高2017年高三年级第三次模拟考试 数学（理科）参考答案 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎ （1）C （2）B （3）C （4）A （5）D （6）B ‎ （7）D （8）C （9）A （10）B （11）A （12）D 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎ （13） （14） （15） （16）①④‎ 三、解答题（本大题共6小题，共70分）‎ ‎（17）（Ⅰ）证明：由已知得，‎ 得， ……………………………………3分 ‎∴，‎ 又，∴，‎ ‎∴是首项为，公差为的等差数列．…………………………………………6分 ‎（Ⅱ）解：由（Ⅰ）知，，‎ ‎∴，． ………………………………………8分 ‎∴，…9分 两边乘以2，得，‎ 两式相减得 ‎，…………………11分 ‎∴． ……………………………………………12分 ‎（18）解：（Ⅰ）根据题意，计算，‎ ‎， ………………………………………2分 ‎， ……………………………4分 ‎，‎ ‎∴关于的回归直线方程； ……………………………6分 ‎（Ⅱ）时，，‎ 预测该店明天的营业额为元； ……………………………………………8分 ‎（Ⅲ）由题意，平均数为，方差为，‎ 所以， …………………………………………………10分 所以，‎ ‎． …………………12分 ‎（19）（Ⅰ）证明：连结交于点，连结．‎ 则是的中点，又为的中点，所以∥， …………………2分 且面，面， ‎ ‎∴∥平面； …………………………………………………4分 ‎（Ⅱ）取的中点，连结，∵点在面上的射影在上，且．‎ ‎∴面， …………………………………………………6分 则可建立如图的空间直角坐标系，设． ……………………7分 ‎∵，，则 ‎，，，‎ ‎，‎ ‎，， ‎ ‎． …………………………………………………9分 设为面的法向量，，‎ 取，则， …………………………………………10分 由与平面所成角的正弦值为，即 ‎，可得． ……………………11分 ‎∴三棱柱的高为，‎ ‎∴． ……………………12分 ‎（20）解：（Ⅰ）由抛物线：（）在第一象限内的点到焦点的距离为 ，得，所以，故抛物线方程为，，………………2分 所以曲线在第一象限的图象对应的函数解析式为，则 故曲线在点处的切线斜率，‎ 切线方程为：，即， ……………………………3分 令得，所以点，‎ 故线段， …………………………………………………4分 ‎（Ⅱ）由题意知：，因为与相交，所以，‎ 设：，令，得，‎ 故， ………………………………………5分 设，‎ 由消去得：，‎ 则， …………………………………………………7分 直线的斜率为， ‎ 同理直线的斜率为，直线的斜率为，…………………8分 因为直线的斜率依次成等差数列，‎ 所以，‎ 即， …………………………………………………10分 因为不经过点，所以，‎ 所以，即，…………………………………………………11分 故：，即恒过定点…………………………………………12分 ‎（21）解：（Ⅰ）当时，，则（），………1分 ‎∴， …………………………………………………2分 ‎∴函数的图象在处的切线方程为，‎ 即． …………………………………………………3分 ‎（Ⅱ）不等式，即，∴，‎ ‎∵，∴恒成立， ……………………………………4分 令（），则，‎ 当时，，单调递增，‎ 当时，，单调递减，‎ ‎∴当时，取得极大值，也为最大值，‎ 故， ……………………………5分 由，得，‎ ‎∴实数的取值范围是． ………………………6分 ‎（Ⅲ）证明：由，‎ 得， …………………………7分 ‎①当时，，单调递增无极值点，不符合题意；………8分 ‎②当或时，令，设的两根为和，‎ ‎∵为函数的极大值点，∴，‎ 由，，知 ，，‎ 又由，得， ………………………………9分 ‎∵（），‎ 令，，则，‎ 令，，则，‎ 当时，，当时，，‎ ‎∴， …………………………………………11分 ‎∴，∴在上单调递减，∴，‎ ‎∴． …………………………………………………12分 ‎（22）解：（Ⅰ）直线：，展开可得：‎ ‎ ，‎ 化为直角坐标方程：，‎ 时，化为：， ……………………………………2分 曲线C：，利用平方关系化为：．……3分 圆心到直线的距离，……………………4分 因此直线与曲线相切． …………………………………………………5分 ‎（Ⅱ）∵曲线上存在到直线的距离等于的点，‎ ‎∴圆心到直线的距离， ………………8分 解得．‎ ‎∴实数的范围是． …………………………………………………10分 ‎（23）解：（Ⅰ）∵函数，‎ ‎ 故函数 的最小值为，‎ ‎ 此时，． …………………………………………………5分 ‎（Ⅱ）当集合，函数恒成立，‎ 即的图象恒位于直线的上方， …………………………6分 函数， ……………………7分 而函数表示过点，斜率为的一条直线，‎ 如图所示：当直线过点时，，∴， ………8分 当直线过点时，，∴， ……………………9分 数形结合可得要求的的范围为．……………………………………10分 ‎【来源：全,品…中&高*考+网】‎